Принципы компьютерного моделирования смо

Основная проблема при составлении алгоритмов на машине с последовательной обработкой процессов состоит в том, что при моделировании необходимо отслеживать множество процессов, которые в реальном времени происходят параллельно. В связи с этим алгоритмы моделирования имеют свои особенности:

• продвижение системы во времени, отслеживание временной координаты;

• обеспечение синхронной работы объектов, из которых состоит моделируемая система.

В настоящий момент известны четыре основных принципа регламентации событий.

• принцип ;

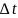• принцип особых состояний;

• принцип последовательной проводки заявок;

• принцип параллельной работы объектов (объектный принцип моделирования).

Принцип Δt

Принцип состоит в том, что алгоритмом моделирования имитируется движение, то есть изменение состояния системы, в фиксированные моменты времен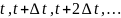и: Изменения системы отслеживаются такт за тактом в заданные моменты. Это наиболее универсальный из рассматриваемых принципов, так как применим к очень широкому классу систем. Он же является наиболее простым в реализации.

Однако это самый неэкономичный принцип, поскольку вся система анализируется моделирующим алгоритмом на каждом такте, даже если в ней не происходит никаких изменений. Кроме того, времена событий округляются до величины Δt, что ведет к погрешностям в определении переменных, характеризующих систему.

Принцип особых состояний

Назовем состояние, в котором обычно находится система, обычным состоянием. Такие состояния интереса не представляют, хотя занимают большую часть времени.

Особые состояния – это такие состояния в изолированные моменты времени, в которых характеристики системы изменяются скачкообразно. Для изменения состояния системы нужна определенная причина, например, приход очередного входного сигнала. Ясно, что с точки зрения моделирования интерес представляет именно изменение характеристик системы, то есть принцип требует отслеживания моментов перехода системы из одного особого состояния в другое.

Принцип последовательной проводки заявок

Принцип состоит в том, что каждая заявка отслеживается от момента поступления ее в систему до момента ее выхода из системы. И только потом рассматривается следующая заявка.

Объектный принцип моделирования

Как правило, алгоритмы, спроектированные по первым трем принципам, плохо модернизируются. А производственная ситуация часто меняется и требует соответствующих моделей для нахождения рациональных решений в процессе управления.

Таким образом, возникла необходимость в приемах моделирования, обеспечивающих независимость составления моделей элементов сложной системы от изменения задачи или структуры производства. Такой подход моделирования отдельных объектов независимо друг от друга позволяет собирать сколь угодно сложные системы без изменения их составляющих. Принцип объектного моделирования обеспечивает модернизацию сложных систем, удлиняя жизненный цикл АСУ.

Задания

1. Моделирование простейшей системы

А. Используя имитационный алгоритмический способ составить модель для задачи с человеком и автобусом, если человек идёт в ту же сторону, что и автобус. Учесть, что Ваши объекты могут никогда не встретиться при каких-то начальных условиях.

Пункты «Б» и «В» – по вариантам:

	Б. Усложнить задачу	В. Сделать возникающие препятствия статистическими
11	Поставить на пути автобуса остановки на 5 минут через каждые x км	Длительность остановок – от 0 до 5 минут
22	Поставить на пути человека ларёк, у которого он задержится на 5 минут	Время на покупку – от 0 до 10 минут
33	Устроить на пути автобуса ремонт дороги, где ему придется снизить скорость до 5 км/час	Длина ремонтируемого участка – от 0 до 10 км
44	Человек, уставая, уменьшает скорость на 10% после каждых 30 минут бега	Человечек нервный, каждые 30 мин то увеличивает, то уменьшает скорость, которая может быть от 3 до 8 км/час
55	Поставить на пути автобуса шлагбаум, который закрыва­ется через каждые 20 минут на 5 минут	Шлагбаум может оказаться и закрытым, и открытым (вероятность закрытости 25%) . Если он закрыт, то откроется через 0-10 минут
66	Устроить человеку увеличение скорости на 2 км/час через X км после его выхода	Увеличение скорости – от 1 до 50%, место ускорения – от 0,5 до 1,5 км от дома

Чтобы использовать датчик случайных чисел, в программе надо использовать Randomize. Функция RND возвращает случайные значения в диапазоне [0; 1[ (ноль возможен, единица – нет). Если нужны целые случайные числа от 3 до 20, например, используйте Sl=Int((20-3)*Rnd+3)