Потоки случайных событий

Когда похожих друг на друга событий много и они следуют друг за другом, то они образуют поток.

Поток событий – это последовательность однородных событий, наступающих одно за другим в случайные промежутки времени. При этом считается, что статистическая характеристика этого явления (интенсивность потока событий) задана.

Интенсивность потока – это среднее число событий в единицу времени.

Поток называют

детерминированным, если интервал между событиями равен константе или определен какой-либо формулой;
случайным, если интервал между событиями – случайная величина;
ординарным, если вероятность одновременного появления двух и более событий равна нулю;
стационарным, если вероятность попадания того или иного числа событий на участок времени длиной  зависит только от длины участка и не зависит от того, где именно на оси времени он находится, т.е. ;
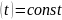потоком без последействия, если вероятность появления случайного события не зависит от момента совершения предыдущих событий.

Если случайный поток ординарен и не имеет последействия, то его называют пуассоновским потоком. Название "пуассоновский" связано с тем, что при таком потоке число событий, попадающих на любой фиксированный интервал времени, будет распределено по закону Пуассона, т.е. вероятность P_m того, что за интервал времени произойдет m событий:

Стационарный пуассоновский поток считают простейшим, для него

(15)

Вероятность P₀ "непоявления" события выразится как если m=0 подставить в формулу (15), а вероятность появления хотя бы одного события:

Важной характеристикой потока является закон распределения длины промежутка между соседними событиями. Пусть T – промежуток времени между двумя соседними событиями в простейшем потоке. Хотелось бы найти F(t) – функцию распределения случайной величины T, т.е. вероятность того, что T<t. Рассмотрим обратную величину , которая является вероятностью того, что T>t или того, что за время T событие не произойдет: Значит, следовательно,

(16)

Закон распределения с плотностью (16) называется показательным законом.

Моделирование простейшего потока

Считаем, что интенсивность потока задана, и ставим задачу смоделировать возникновение событий через временные интервалы, распределенные по закону (16). Воспользуемся методом ступенчатой аппроксимации (рис. 16), считая, что после некоторого t_max значения f(t) пренебрежимо малы.

Разбиваем интервал (0; t_max) на n интервалов длиной t, а интервал (0;1), в который попадают случайные числа, на n интервалов, длина каждого из которых определяется как Но т.к.