
- •Основные понятия теории моделирования Моделирование как метод научного познания
- •Понятие модели и моделирования
- •Понятие информационной модели
- •Виды моделирования
- •Математическое и компьютерное моделирование
- •Пример моделирования простейшей системы
- •Формализация систем и классификация моделей Некоторые термины системного анализа
- •Формальная модель объекта.
- •Классификация моделей
- •Основные требования к математическим моделям
- •Этапы процесса моделирования
- •Статические регрессионные модели Понятие черного ящика и регрессии
- •Линейная одномерная регрессионная модель
- •Линейная множественная регрессионная модель
- •Нелинейные регрессионные модели
- •Динамические модели Динамические системы
- •Динамическая система первого порядка
- •Звено второго порядка (колебательное звено)
- •Динамические регрессионные модели
- •Модель в виде фильтра Каллмана
- •Статистическое моделирование Понятие статистического моделирования
- •Метод Монте-Карло.
- •Генераторы случайных чисел
- •Проверка качества работы генератора
- •Моделирование случайной величины с заданным законом распределения
- •Моделирование системы случайных величин
- •Потоки случайных событий
- •Системы массового обслуживания (смо)
- •Принципы компьютерного моделирования смо
- •Задания
- •1. Моделирование простейшей системы
- •2. Статическая регрессионная модель
- •3. Динамическая регрессионная модель
- •4. Метод Монте-Карло и генераторы случайных чисел
- •5. Моделирование смо
- •Приложения
- •Нормальный закон распределения (закон Гаусса)
- •Распределение Пуассона
- •Список источников
- •Моделирование процессов и систем
- •153000 Г. Иваново, пр. Ф. Энгельса, 21 Оглавление
Моделирование случайной величины с заданным законом распределения
Основные сведения о законах распределения случайных величин можно найти в приложении 3. Так как законы распределения вероятности событий могут быть различными, приходится превращать равномерный ГСЧ в генератор случайных чисел с заданным законом распределения.
Метод ступенчатой аппроксимации
П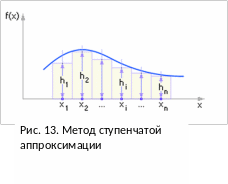 усть
f(x)
на рис. 13 – это распределение вероятности.
hi
– высота i-го
столбца, пропорционально вероятности
появления значений x
из интервала
усть
f(x)
на рис. 13 – это распределение вероятности.
hi
– высота i-го
столбца, пропорционально вероятности
появления значений x
из интервала
 .
.
Операция
нормировки обеспечивает равенство
единице суммы вероятностей всех n
событий:
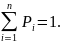 Операцией нормировки значения h
переводим в единицы вероятности:
Операцией нормировки значения h
переводим в единицы вероятности:

Интервал
(0;1) разбивается на n
промежутков разной длины (длина i-го
промежутка равна
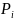 ).
Считается, что случайная величина
приняла значение
).
Считается, что случайная величина
приняла значение
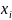 ,
если сгенерированное датчиком число
попало в i-й
интервал.
,
если сгенерированное датчиком число
попало в i-й
интервал.
Необходимо отметить, метод огрубляет изначальную постановку задачи, т.к. внутри каждого интервала значения x неразличимы.
Метод усечения
М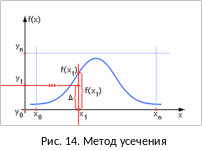 етод
используется в случае, когда функция
задана аналитически (в виде формулы).
График функции вписывают в прямоугольник
(см. рис. 14) На оси X и
Y подают случайные равномерно
распределенные числа в диапазонах
етод
используется в случае, когда функция
задана аналитически (в виде формулы).
График функции вписывают в прямоугольник
(см. рис. 14) На оси X и
Y подают случайные равномерно
распределенные числа в диапазонах
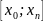 и
и
 ,
соответственно.
,
соответственно.
Если точка в пересечении этих двух координат лежит ниже кривой плотности вероятности, то событие X произошло, иначе нет.
Моделирование нормально распределенных случайных величин
Естественно, при моделировании нормально распределенной случайной величины можно воспользоваться общими методами (методом усечения, например). Но для нормального закона разработаны отдельные эффективные методы моделирования.
1. Использование центральной предельной теоремы.
Общая идея метода следующая: требуется сложить случайные числа с любым законом распределения, нормализовать их и перевести в нужный диапазон нормального распределения.
Допустим, надо получить ряд случайных чисел x, распределенных по нормальному закону с математическим ожиданием mx и среднеквадратичным отклонением σx.
А. Сложим n случайных чисел, используя стандартный ГСЧ:
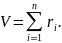
Согласно
центральной предельной теореме числа
V образуют ряд значений, распределенный
по нормальному закону. Эти числа тем
лучше описывают нормальный закон, чем
больше параметр n (на практике n
берут равными 6 или 12). Закон распределения
чисел V имеет математическое ожидание
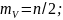
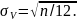
Поэтому он является смещенным относительно заданного произвольного.
Б. С
помощью формулы
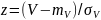 нормализуем этот ряд. Получим
нормализованный закон нормального
распределения чисел Z.
нормализуем этот ряд. Получим
нормализованный закон нормального
распределения чисел Z.
В.
Формулой
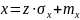 (сдвиг на mx и масштабирование
на σx) преобразуем ряд Z
в ряд x.
(сдвиг на mx и масштабирование
на σx) преобразуем ряд Z
в ряд x.
2. Метод Мюллера
Совсем простым методом получения нормальных чисел является метод Мюллера, использующий формулы:
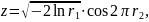 или
или
 где
r1 и r2
– равномерно распределенные случайные
числа из диапазона [0;1].
где
r1 и r2
– равномерно распределенные случайные
числа из диапазона [0;1].
Моделирование системы случайных величин
Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая величина.
Степень
зависимости одной случайной величины
от другой может характеризовать так
называемый коэффициент корреляции
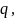 который
определяет степень тесноты линейной
зависимости между величинами (см. рис.
15).
который
определяет степень тесноты линейной
зависимости между величинами (см. рис.
15).
Если
X
и Y
связаны функционально (одному значению
X
соответствует одно определенное значение
Y,
т.е. Y=aX+b),
то
 (в зависимости от знака a).
Если же X
и Y
связаны вероятностной зависимостью
(зависимость веса человека от его роста,
например), то
(в зависимости от знака a).
Если же X
и Y
связаны вероятностной зависимостью
(зависимость веса человека от его роста,
например), то
 ,
причем в случае независимых случайных
величин
,
причем в случае независимых случайных
величин
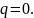

Алгоритм моделирования двух зависимых случайных событий
Пусть
X и Y распределены
по нормальному закону с определенными
значениями mx,
σx и my,
σy. Задан
коэффициент корреляции двух случайных
событий
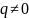 ,
т.е. Y не совсем случайно.
,
т.е. Y не совсем случайно.
Тогда возможный алгоритм реализации модели будет следующим.
Разыгрывается шесть случайных равномерно распределенных на интервале [0;1] чисел; находится их сумма S. Находится нормально распределенное случайное число x по следующей формуле:
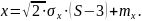
По формуле
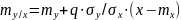 находится математическое ожидание
my/x
(знак y/x
означает, что y будет принимать
случайные значения с учетом условия,
что x уже принял какие-то
определенные значения).
находится математическое ожидание
my/x
(знак y/x
означает, что y будет принимать
случайные значения с учетом условия,
что x уже принял какие-то
определенные значения).
По формуле
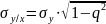 находится среднеквадратическое
отклонение σy/x.
находится среднеквадратическое
отклонение σy/x.Разыгрывается шесть случайных равномерно распределенных на интервале [0;1] чисел и находится их сумма k. Находится нормально распределенное случайное число y по формуле:
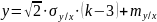 .
.
