Генераторы случайных чисел

В основе метода Монте-Карло лежит генерация случайных чисел, которые должны быть равномерно распределены в интервале (0;1). Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи может оказаться неверным. Поэтому проблема использования генератора действительно случайных и действительно равномерно распределенных чисел стоит очень остро.

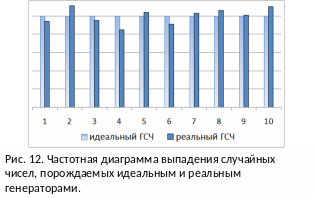
За эталон генератора случайных чисел (ГСЧ) принят такой генератор, который порождает последовательность случайных чисел с равномерным законом распределения. Если наблюдать такой ГСЧ достаточно длительное время, то окажется, что в каждый из десяти, например, интервалов (0;0.1), (0.1;0.2), …, (0.9;1) попадет одинаковое количество случайных чисел (рис. 12).

Генераторы случайных чисел по способу получения чисел делятся

• на физические (монета, игральные кости, рулетка, генератор шума);

• табличные (специальным образом составленные таблицы, содержащие проверенные некоррелированные¹ цифры);

• алгоритмические.

Числа, генерируемые с помощью алгоритмических ГСЧ, всегда являются псевдослучайными, то есть каждое последующее сгенерированное число зависит от предыдущего: Последовательности, составленные из таких чисел, образуют петли, т.е. обязательно существует цикл (период), повторяющийся бесконечное число раз.

Проверка качества работы генератора

От качества работы ГСЧ зависит качество работы всей системы и точность результатов. Поэтому случайная последовательность, порождаемая ГСЧ, должна удовлетворять целому ряду критериев.

Осуществляемые проверки бывают двух типов:

• проверки на равномерность распределения;

• проверки на статистическую независимость.

Проверки на равномерность распределения

1. ГСЧ должен выдавать близкие к следующим значения статистических параметров, характерных для равномерного случайного закона

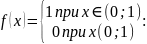
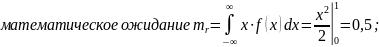
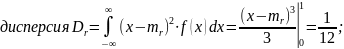
2. Частотный тест

Частотный тест позволяет выяснить, сколько чисел попало в интервал 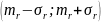, где (в хорошем ГСЧ в этот интервал должно попадать около 57,7% всех чисел).

Кроме того, количество чисел, попавших в интервал (0; 0.5), должно быть примерно равно количеству чисел, попавших в интервал (0.5; 1).

3. Проверка по критерию «хи-квадрат» (критерию Пирсона)

Критерий 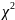, предложенный в 1900 году Карлом Пирсоном, является основным критерием, используемым для проверки, удовлетворяет ли рассматриваемая случайная величина заданному закону распределения.

Поскольку закон распределения идеального ГСЧ равномерный, и теоретическая вероятность попадания чисел в i-й интервал равна 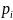, то в каждый из k интервалов попадет ровно по 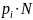чисел, если N – общее количество сгенерированных чисел. При работе реального ГСЧ в каждый интервал попадет 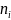чисел. Критерий для экспериментальных данных выражается как

(12)

Можно несколько упростить это выражение:

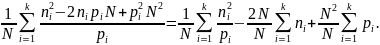
			(13)
		(14)

Для распределения составлены специальные таблицы (см. приложение 2). Как видно из таблицы приложения 2, распределение зависит от параметра , называемого числом степеней свободы. Число равно количеству разрядов k минус число независимых условий ("связей"), наложенных на частоты. Требование (13), т.е. требование того, чтобы сумма частот была равна единице, накладывается во всех случаях. Если этим набор условий ограничивается, то

Пользуясь таблицами можно оценить степень согласованности теоретического и статистического распределений. Если случайная величина действительно распределена по закону F (в нашем случае – равномерно), то найденная по таблице вероятность 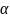есть вероятность того, что за счет чисто случайных причин мера расхождения теоретического и статистического (реального) распределений будет не меньше, чем полученное в серии опытов значение . Пример использования найденных значений и теоретических значений, собранных в таблицах, приведен в приложении 2.

Итак, процедура проверки имеет следующий вид:

• диапазон от 0 до 1 разбивается на k равных интервалов;

• запускается ГСЧ N раз (N должно быть велико, например, );

• определяется количество случайных чисел, попавших в каждый интервал ( );

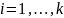• вычисляется экспериментальное значение χ²_эксп. по формуле (12) или (14);

• путем сравнения экспериментально полученного значения с теоретическим из табл. 1 делается вывод о пригодности генератора для использования.

Если найденная по таблицам вероятность мала, то гипотеза о том, что ГСЧ выдает равномерно распределенные числа отбрасывается как неправдоподобная. Если же χ²_эксп. очень мало, то разумно признать, что столь близкое совпадение обусловлено не идеальностью генератора, а "неслучайностью" полученных чисел. Есть мнение, что чем ближе к значению 50%, тем лучше.

Проверки на статистическую независимость

1. Проверка на частоту появления цифры в последовательности.

Случайное число состоит из цифр. Имеет смысл, рассматривая несколько полученных подряд случайных чисел, проверить частоту появления каждой цифры по критерию .

2. Проверка появления серий из одинаковых цифр.

Например, в последовательности «24633899915467766618» есть 2 серии длиной в 2 символа (33 и 77) и 2 серии длиной в 3 символа (999 и 666).

Вероятность 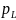появления серии длиной в L равна .

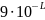Частота появления серий проверяется по критерию с использованием значений .