Модель в виде фильтра Каллмана

Каллманом была доказана теорема о том, что любой динамический сигнал может быть представлен в виде:

(11)

Идея фильтра Каллмана заключается в том, что выход системы в i-й момент времени определяется входным сигналом, его предысторией и предысторией самого состояния системы.

Чем больше имеется членов ряда, то есть чем больше переменных Y учитывается в записи модели, тем глубже память системы. Заметим, что наличие члена 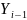в модели динамической системы (11) соответствует наличию первой производной, 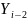– второй производной и т. д.

Ошибка между значением экспериментально снятой точки и теоретическим ее значением (гипотезой) выразится как:

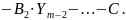
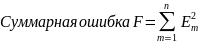
должна быть минимизирована относительно определяемых переменных A₁, A₂, …, B₁, B₂, …, C:

Если взять частные производные от F по параметрам A₁, A₂, …, B₁, B₂, …, C и приравнять их к нулю, получим линейную множественную регрессионную модель, из которой определяются неизвестные коэффициенты уравнения (11).

Статистическое моделирование Понятие статистического моделирования

Статистическое моделирование используется при исследовании сложных систем, подверженных случайным возмущениям. Возможно построение вероятностных аналитических моделей и вероятностных имитационных моделей.

В вероятностных аналитических моделях влияние случайных факторов учитывается с помощью задания вероятностных характеристик случайных процессов (законов распределения вероятностей, например). Поскольку построение таких моделей представляет собой сложную вычислительную задачу, вероятностное аналитическое моделирование используют для изучения сравнительно простых систем.

Подмечено, что введение случайных возмущений в имитационные модели не вносит принципиальных усложнений, поэтому исследование сложных случайных процессов проводится, как правило, на имитационных моделях.

В вероятностном имитационном моделировании оперируют не характеристиками случайных процессов, а конкретными случайными числами – значениями параметров. Следовательно, результаты, полученные на имитационной модели, являются случайными реализациями. Поэтому для нахождения объективных и устойчивых характеристик процесса требуется многократное воспроизведение компьютерного эксперимента с последующей статистической обработкой полученных данных. Именно по этой причине исследование с помощью вероятностного имитационного моделирования принято называть статистическим моделированием.

Итак, статистическое моделирование – это способ изучения сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационных моделей.

В основе статистического моделирования лежит метод Монте-Карло.

Метод Монте-Карло.

Сначала Энрико Ферми в 1930-х годах в Италии, а затем Джон фон Нейман и Станислав Улам в 1940-х в Лос-Аламосе предложили использовать стохастический подход для аппроксимации многомерных интегралов.

Идея была развита Уламом, который вынужденно бездельничал во время болезни, и, раскладывая пасьянсы, задался вопросом, какова вероятность того, что пасьянс «сложится». Ему в голову пришла идея, что вместо того, чтобы использовать соображения комбинаторики, можно просто поставить «эксперимент» большое число раз и, подсчитав число удачных исходов, оценить их вероятность.

Годом рождения метода считается 1949 год, когда в свет вышла статья Метрополиса и Улама «Метод Монте-Карло»¹.

Появление электронных компьютеров, которые могли с большой скоростью генерировать псевдослучайные числа, резко расширило круг задач, для решения которых стохастический подход оказался более эффективным, чем другие математические методы.

Использование метода заключается в многократном повторении компьютерного эксперимента и статистическом анализе полученной серии результатов.

Р ассмотрим вычисление интеграла методом Монте-Карло (рис. 10). Пусть задана некоторая функция 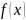. Задача состоит в том, чтобы определить 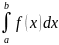, т.е. найти площадь под графиком на рис. 10.

Ограничиваем кривую прямоугольником поиска и распределяем в нем точки случайным образом. Если 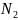– количество точек под кривой, а – общее количество точек, то

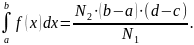
Метод Монте-Карло эффективен и прост, но необходим «хороший» генератор случайных чисел. Вторая проблема заключается в определении количества точек, необходимых для обеспечения решения с заданной точностью (объема выборки). Эксперименты показывают, что точность примерно пропорциональна корню квадратному из объема выборки: чтобы увеличить точность в 10 раз, объем выборки нужно увеличить в 100 раз.

Схема статистического эксперимента

С хема использования метода Монте-Карло при исследовании систем со случайными параметрами представлена на рис. 11.

Построив модель системы со случайными параметрами, на ее вход подают входные сигналы от генератора случайных чисел. Он устроен так, что выдает равномерно распределенные случайные числа из интервала [0;1]. Так как одни события могут быть более вероятными, другие – менее вероятными, то равномерно распределенные случайные числа от генератора подают на преобразователь закона случайных чисел, который преобразует их в заданный пользователем закон распределения вероятности, например, в нормальный или экспоненциальный закон. Эти преобразованные случайные числа x подают на вход модели.

Модель отрабатывает входной сигнал x по некоторому закону y = φ(x) и получает выходной сигнал y, который также является случайным.

В блоке накопления статистики установлены фильтры и счетчики. Фильтр (некоторое логическое условие) определяет по значению y, реализовалось ли в конкретном опыте некоторое событие (выполнилось или не выполнилось некое условие). Если событие реализовалось, то счетчик события N_i увеличивается на единицу. Если требуется следить за несколькими разными типами событий, то для статистического моделирования понадобится несколько фильтров и счетчиков. Всегда ведется подсчет количества экспериментов N.

Далее отношение N_i к N дает оценку вероятности p_i появления события i, то есть указывает на частоту его выпадения в серии из N опытов. Это позволяет сделать выводы о статистических свойствах моделируемого объекта.

Например, событие A совершилось в результате проведенных 200 экспериментов 50 раз. Это означает, что вероятность совершения события равна 0,25. Вероятность того, что событие не совершится, равна, соответственно, 1 – 0,25 = 0,75.