5. Основные положения теории Маковица
В статье Гарри Марковица впервые была предложена математическая модель формирования оптимального портфеля ценных бумаг и были приведены методы построения портфелей при определенных условиях. Нобелевская премия по экономике была присуждена Марковичу в 1990 году, значительно позже выхода в свет его работ.
В основе теории Марковица лежит предпосылка о том, что инвестор покупает ценную бумагу на некоторый промежуток времени, ожидаемая доходность и стандартное отклонение портфеля являются основными критериями для инвестора при выборе оптимального портфеля. Инвестор заинтересован в бумагах с наибольшей доходностью и наименьшим риском. Учет взаимных корреляционных зависимостей между доходностями ценных бумаг позволяет проводить эффективную диверсификацию портфеля, приводящую к существенному снижению риска портфеля по сравнению с риском включенных в него операций. Для того чтобы рассчитать риск и доходность инвестиционного портфеля, инвестор оценивает ожидаемые доходности, стандартные отклонения и корреляцию между рассматриваемыми ценными бумагами; выбирает портфель с наибольшей доходностью и наименьшим риском. Для этого ему необходимо установить связь между ожидаемыми доходностями ценных бумаг и ожидаемой доходностью портфеля, составленного из этих ценных бумаг; далее установить связь между стандартными отклонениями ценных бумаг и портфеля.
Процедура выбора нивестиц.портфеля
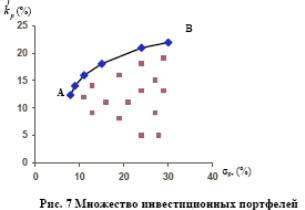
Если взять все активы и все возможные их комбинации (портфели), то мы получим некоторое множество портфелей (Рис.7). Любой из них находится внутри этого множества.
Рациональный инвестор для заданного уровня риска выбирает портфель, по которому ожидается более высокая доходность. Поэтому, эффективные портфели находятся на кривой АВ, огибающей множество допустимых портфелей, которая называется эффективной границей.
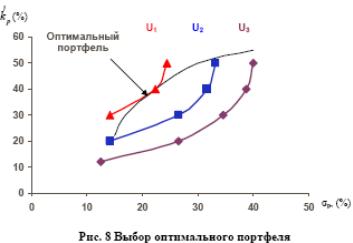
Инвесторы, формирующие портфель только из рисковых ценных бумаг, будут выбирать конкретный портфель из множества эффективных в зависимости от их отношения к риску. При графическом рассмотрении этот портфель будет точкой касания кривой безразличия инвестора с множеством эффективных портфелей (Рис.8).
Оптимальный портфель инвестора c кривыми безразличия U1, U2,и U3 находится в точке касания кривой безразличия U1 и эффективной границы. В этой точке линия инвестиционных возможностей касается наивысшей из возможных кривых безразличия. Для каждого инвестора выбор оптимального портфеля будет индивидуальным, т.к. индивидуальны кривые безразличия. Множество инвестиционных портфелей определяется рынком и не зависит от предпочтений инвестора.
8. Модель оценки финансовых активов (сарм)
В середине 60-х годов Уильям Шарп и Джон Линтнер предложили модель оценки финансовых активов (Сapital Asset Pricing Model - CAPM).
Предпосылки САРМ:
1) все инвесторы максимизируют свою ожидаемую полезность;
2) учитывается один период одинаковый для всех инвесторов;
3) выбор из альтернативных вариантов инвестирования осуществляется по соотношению ожидаемой доходности и риска;
4) инвесторы – противники риска;
5) все инвесторы владеют одинаковой информацией о риске активов;
6) на рынке имеются неограниченные возможности инвестирования и займа по единой безрисковой ставке;
7) отсутствуют трансакционные издержки;
8) одинаковое налогообложение дивидендов и прироста капитала;
9) отсутствует возможность влияния на рыночную цену актива отдельными инвесторами;
10) все активы высоколиквидны и бесконечно делимы.
В теории CARM рискованность ценной бумаги измеряется её B-коэффициентом. Этот коэффициент характеризует изменчивость доходности конкрентной акции относительно доходности рынка ценных бумаг.
По определению некая «средняя акция» имеет В=1,0; акция изменчивость доходности которой выше чем в среднем на рынке имеет В>1,0; акция изменчивость доходности которой меньше чем в среднем на рынке имеет В<1,0
Уравнение связи между риском акции и доходностью акции называется уравнением «линии рынка ценных бумаг»:
Ai=Arf+(Am-Arf)*Bi, где
Ai – требуемая доходность i-акции
Arf – безрисковая доходность в качестве которой на многих фондовых рынках принимают доходность облигации казначейства США
Am – требуемая доходность рыночного портфеля состоящая из всех акции
(Am-Arf)*Bi – это премия за риск владения i-акцией, она вальирует в зависимости от того является ли данная акция более или менее рисковой по сравнению с другими, имеет ли она большее или меньшее значение B-коэффициента.
Требуемая доходность зависит не только от рыночного риска измеряемого B-коэффициентом, но и от безрисковой ставки доходности и премии за рыночный риск.
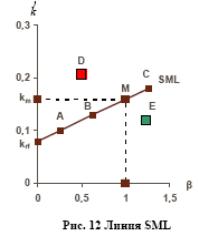
Экономический смысл наклона прямой SML отражает отношение к риску на данном рынке. Чем меньше средний инвестор склонен к риску, тем больше премия за риск и требуемая доходность по всем рисковым активам. А, следовательно, больше угол наклона прямой SML. Эта зависимость, представленная графически, носит название линии рынка ценных бумаг (SML). По оси абсцисс откладывается β-коэффициент, по оси ординат – ожидаемая доходность инвестора с учетом риска (Рис. 12). Наклон прямой SML отражает отношение инвесторов к риску на данном рынке. Прямая SML отражает выбор среднего инвестора в равновесии, когда требуемая доходность по акции равна ожидаемой доходности. Ожидаемая доходность по акции D превышает требуемую, следовательно акции недооценены. Повышение спроса на акции приведет к росту цены и падению ожидаемой доходности. Покупка акций D прекратится, когда ожидаемая доходность сравняется с требуемой, и установится равновесие. Это равновесие отражает прямая SML. Обратная ситуация характерна для акции Е. Она переоценена. Продажи акции приведут к падению ее цены и росту доходности.
Влияние инфляции. Оно сказывается в теории САРМ на доходности всех активов одинаково, поэтому линия рын¬ка ценных бумаг поднимается по шкале ставок доходности на величину инфляционной премии.
Изменение отношения к риску. Крутизна линии рынка ценных бумаг отражает отношение инвесторов к риску: чем круче наклон линии, тем в большей степени они пытаются элиминировать риск.
Изменение бета-коэф акции. Фирма может изме¬нять рискованность своих ценных бумаг, а следовательно, и значение бета-коэф за счет изменения структуры своих активов, использования внешних источников финансирования. Бета-коэф может меняться и в результате воздей¬ствия рыночных факторов, например изменения конку-ренции в отрасли. Когда происходят подобные изменения, меняется и требуемая доходность, что влияет и на цену акций фирмы.
Факторы, оказывающие влияние на положение прямой SML