69) Формула нахождения обратной матрицы

70) Решение матричного уравнения АХ=В с помощью обратной матрицы.

Матричные уравнения могут иметь вид:

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Например, чтобы найти матрицу   из уравнения  , необходимо умножить это уравнение на   слева.

Тогда:

Следовательно, чтобы найти решение   уравнения  , нужно найти обратную матрицу  и умножить ее на матрицу  , стоящие в правой части уравнения.

Аналогично решаются другие уравнения.

71) Базисный минор матрицы. Опр.

 В матрице порядка mn минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.

Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.

            В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

72)Ранг матрицы. Опр.

73) Теорема о базисном миноре

Любой столбец матрицы А может быть предст. в виде лин.комбинации базисных столбцов (тех, кот. пересекают базисный минор)

74) Система линейных алгебраических уравнений. Общие понятия.

СЛАУ наз. ОДНОРОДНОЙ, если все свободные члены равны 0!

75) Теорема Крамера

- опред.А i – получен из  заменой i-столбца на столбец свободных членов

76) Т. Кронекера- Капелли

77) Каноническое уравнение эллипса. Геометрический смысл коэффициентов

.

Геометрический смысл коэффициентов в уравнении эллипса

Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение  , находим точки пересечения эллипса с осью абсцисс (с фокальной осью):  . Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна  . Этот отрезок, как отмечено выше, называется большой осью эллипса, а число   — большой полуосью эллипса. Подставляя  , получаем  . Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна  . Этот отрезок называется малой осью эллипса, а число   — малой полуосью эллипса.

Действительно,  , причем равенство   получается только в случае  , когда эллипс является окружностью. Отношение   называется коэффициентом сжатия эллипса.

78) Каноническое уравнение окружности

Окружность радиуса R с центром в начале координат

Окружность радиуса R с центром в точке C(a; b):

79) Каноническое уравнение гиперболы . Геометрический смысл коэффициентов

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение  , находим абсциссы точек пересечения:  . Следовательно, вершины имеют координаты  . Длина отрезка, соединяющего вершины, равна  . Этот отрезок называется действительной осью гиперболы, а число   — действительной полуосью гиперболы. Подставляя  , получаем  . Длина отрезка оси ординат, соединяющего точки  , равна  . Этот отрезок называется мнимой осью гиперболы, а число   — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

80) Каноническое уравнение параболы . Геометрический смысл коэффициентов

Геометрический смысл параметра в уравнении параболы

Поясним геометрический смысл параметра   в каноническом уравнении параболы. Подставляя в уравнение (3.51)  , получаем  , т.е.   . Следовательно, параметр   — это половина длины хорды параболы, проходящей через её фокус перпендикулярно оси параболы.

Фокальным параметром параболы, так же как для эллипса и для гиперболы, называется половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси (см. рис.3.45,в). Из уравнения параболы в полярных координатах при   получаем  , т.е. параметр параболы совпадает с её фокальным параметром.

81) Многочлены. Т. Базу

82) Формулировка основной Т. алгебры

Всякое алг. ур-ие степени n>=1 имеет хотя бы 1 корень (Вещественный или комплексный)

83) Понятие комплексного числа. Мнимая единица.

84) Алгебраическая форма компл.числа

x= ReZ (действ.часть к.ч.)

y= Im Z (мнимая часть)

85) Изображение к.ч на комплексной плоскости.

86) Операция сложения комплексных чисел

87)

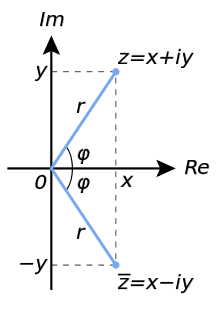
88) Комплексно сопряженные числа. Изображение на комплексной плоскости.

Если комплексное число  , то число   называется сопряжённым(или комплексно сопряжённым) к   (обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.

Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.

•  (сопряжённое к сопряжённому есть исходное).

• 

• 

• 

• 

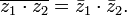
Обобщение:  , где   — произвольный многочлен с вещественными коэффициентами.

• 

• 

89) Операция деления к.ч в алгебраической форме. Алгоритм.

90) Тригонометрическая форма к.ч. Модуль и аргумент к.ч.

91) Связь между алг. и тригон. формами к.ч.

92) Операция умн. к.ч в тригон.форме

93) Операция деления в тригон.форме

94) Операция возв. в степень в тригон.форме

95) Показательная форма комп.числа

96) Формула Эйлера

97) Связь между тригон.и показательной формами к.ч.

98) Операция умножения к.ч. в показательной форме

Найдем произведение комплексных чисел   и  , представленных в показательной форме:

   

Таким образом, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.

99) Операция деления к.ч. в показательной форме

Аналогично находится частное от деления комплексных чисел   и  :

   

Чтобы разделить одно комплексное число на другое, нужно модуль первого числа разделить на модуль второго и из аргумента первого числа вычесть аргумент второго.