10.4.3. Компьютерные алгоритмы шифрования

Существует множество алгоритмов шифрования, реализованных в виде компьютерных программ:

- DES (Data Encryption Standard), AES. Симметричный алгоритм шифрования(госстанд. в США).

- ГОСТ 28147-89. Симметричный алгоритм шифрования (госстандарт в России).

- RSA(Rivest, Shamir, Adleman,1978 г.). Асимметричный алгоритм шифрования.

Алгоритм DES (госстандарт в США, 1980г.) Параметры алгоритма: разрядность блока - 64 бита, размер ключа - 56 бит (с учетом контрольных разрядов - 64 бита). Алгоритм представляет собой классическую сеть Файстеля из 16 раундов с добавлением входной и выходной перестановки бит).

Образующая функция сети в алгоритме DES состоит из 4 операций:

1) перестановка бит/расширение блока с помощью повторов по определенной схеме;

2) наложение ключа раунда операцией XOR;

3) табличные подстановки;

4) перестановка бит.

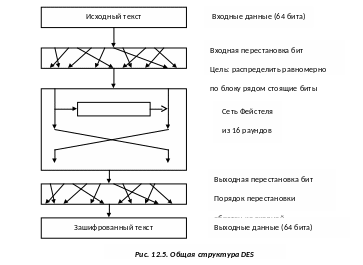
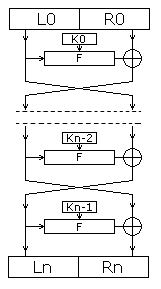
Рис.12.6. Сеть Фейстеля

Раунд - один шаг шифрования в шифре Фейстеля и близких ему по архитектуре шифрах, в ходе которого одна или несколько частей шифруемого блока данных подвергается модификации. Раундовый ключ - секретный элемент, получаемый из ключа криптоалгоритма и используемый шифром Фейстеля и аналогичными криптоалгоритмами на одном раунде шифрования.

Недостаточная длина ключа DES, его ориентированность на аппаратную реализацию побудило правительство США к объявлению открытого конкурса на криптостандарт блочного шифрования США. Конкурс получил название AES (Advanced Encryption Standart) – "улучшенный стандарт шифрования" и был проведен в 1997 - 2000 годах (15 исследовательских групп). Выбраны 5–ть финалистов, прошедших во второй этап конкурса.

Преимущество	Алгоритмы
	RIJNDAEL	SERPENT	TWOFISH	RC6	MARS
Быстродействие: аппаратная реализация	+	+
программная реализация: на слабых ВС на мощных ВС	+	+		+ +
Этап расширения ключа	+		+
Распараллели-ваемость	+
Этап дешифрирования			+	+	+
Запас криптостойкости	Оптимум	Завышен	Завышен	Оптимум	Завышен
Количество голосов	86	59	31	23	13

2 октября 2000 года алгоритм RIJNDAEL был официально признан победителем конкурса и получил название - AES. Структура: прямоугольные KASLT - сети. Шифруемый блок представляется в виде прямоугольника - 44 или 4 6 байт, а затем над ним построчно, по столбцам и побайтно производятся криптопреобразования. KASLT представляет собой аббревиатуру Key Addition (добавление ключа), Substitution (табличная подстановка) и Linear Transposition ( линейное перемешивание).

Rijndael (бельгийцы Vincent Rijmen и Joan Daemen) - шифр с изменяемым размером блока и длиной ключа. Единственные налагаемые требования на эти два параметра - их кратность 32 битам. Размер блока далее определяется как Nb32, длина ключа - Nk32. Количество раундов сети, необходимое для стойкого шифрования зависит от двух параметров. Для конкурса AES в соответствии с требованиями авторы зафиксировали Nb = 4 (то есть шифруемый блок представляет собой квадрат 4 на 4 байта) и Nk = 4, 6, и 8. В этом случае количество раундов сети Nr соответственно равно 10, 12 и 14. Потенциально шифр может работать и с большими по размерам блоками.

К достоинствам алгоритма необходимо отнести очень хорошее быстродействие на всех платформах от 8- до 64-битных. Структура шифра позволяет использовать его при любых комбинациях размера блока и длины ключа - единственным необходимым изменением будет только смена количества раундов.

Возможность распараллеливания у Rijndael очень высокая по сравнению с другими конкурсантами. Коэффициент ускорения вычислений при наличии неограниченного (но разумного) числа процессоров в системе у Rijndael достигает 6-8 раз, что более чем в два раза выше ближайшего соперника.

Перечисленные преимущества - заслуга архитектуры KASLT по сравнению с ограниченными возможностями сети Фейстеля. KASLT - шифр с надежно доказанной криптостойкостью при малом числе раундов. К недостаткам шифра относят необходимость разработки двух независимых процедур - шифрования и дешифрования (объединить их, как в сети Фейстеля, уже невозможно).

ГОСТ 28147-89 - российский стандарт симметричного шифрования (1990г.) - блочный шифр с 256-битным ключом и 32 циклами преобразования, оперирующий 64-битными блоками. Основа алгоритма шифра - сеть Фейстеля. Базовым режимом шифрования является режим простой замены. Для зашифрования - открытый текст разбивается на две половины: младшие биты - A, старшие биты - B. На i-ом цикле используется подключ K_i:

( - двоичное «исключающее или» - XOR)

Оператор XOR имеет следующую таблицу истинности:

XOR	0	1
0	0	1
1	1	0

Результат операции XOR равен TRUE (истина) тогда и только тогда, когда один оператор равен TRUE, а второй - FALSE(ложь). Это дает XOR уникальные свойства: если выполнить операцию XOR над двумя байтами, один из которых называется ключом, а затем взять результат и ключ и снова применить к ним операцию XOR, то в результате получим исходный байт, как показано ниже.

	1101 1001	исходный текст
XOR	0101 0011	ключ
	1000 1010	шифр
	1000 1010	шифр
XOR	0101 0011	ключ
	1101 1001	исходный текст

Для генерации подключей исходный 256-битный ключ разбивается на восемь 32-битных блоков: K₁…K₈.

Ключи K₉…K₂₄ являются циклическим повторением ключей K₁…K₈ (нумеруются от младших битов к старшим). Ключи K₂₅…K₃₂ являются ключами K₁…K₈, идущими в обратном порядке.

После выполнения всех 32 раундов алгоритма, блоки A₃₃ и B₃₃ склеиваются (старшим битом становится A₃₃, а младшим - B₃₃) - результат работы алгоритма.

Расшифрование выполняется так же, как и зашифрование, но инвертируется порядок подключей K_i.

Функция f(A_i,K_i) вычисляется следующим образом:

A_i и K_i складываются по модулю 2³².

Результат разбивается на восемь 4-битовых подпоследовательностей, каждая из которых поступает на вход своего узла таблицы замен (в порядке возрастания старшинства битов), называемого S-блоком. Общее количество S-блоков - восемь, сколько и подпоследовательностей. Каждый S-блок представляет собой перестановку чисел от 0 до 15. Первая 4-битная подпоследовательность попадает на вход первого S-блока, вторая — на вход второго.

Если S-блок выглядит так:

1, 15, 13, 0, 5, 7, 10, 4, 9, 2, 3, 14, 6, 11, 8, 12

и на входе S-блока 0, то на выходе будет 1, если 4, то на выходе будет 5, если на входе 12, то на выходе 6. Выходы всех восьми S-блоков объединяются в 32-битное слово, затем всё слово циклически сдвигается влево (к старшим разрядам) на 11 битов.

RSA. В основе любой схемы асимметричного шифрования лежит определенная трудноразрешимая математическая задача. При этом к данной задаче на самом деле есть способ найти решение, но для этого нужно обладать некоторой дополнительной информацией - ее называют trapdoor – потайная дверь.

В качестве открытого ключа в ассиметричной криптографии выбирается какое-либо частное уравнение, которое и является этой трудноразрешимой задачей. Но при составлении этого уравнения оно разрабатывалось так, что лицо, знающее некоторую дополнительную информацию об этом уравнении, может решить его за разумный временной интервал. Эта дополнительная информация и является закрытым ключом.

В идеальном случае при наличии закрытого ключа и при соответствующем выборе всех параметров задачи процедура шифрования длится доли секунды, а вот на взлом их без знания секретного ключа требуются десятилетия.

При асимметричном шифровании получатель сообщения публикует в качестве открытого ключа часть параметров уравнения, которое только он, зная закрытый ключ, сможет разрешить. Отправитель сообщения делит сообщение на блоки необходимой длины, преобразует их в большие натуральные числа и тем самым заканчивает формирование уравнения. В качестве шифровки посылаются некоторые параметры уравнения, чего недостаточно для злоумышленника, чтобы восстановить исходное послание. Однако их достаточно для получателя, чтобы решить с помощью закрытого ключа уравнение и восстановить добавленный отправителем параметр, который и является исходным текстом.

Процедуры асимметричного шифрования очень медленны. Этот недостаток нейтрализуется объединением асимметричного шифрования с блочными шифрами. Весь текст сообщения преобразуется обычным блочным шифром (намного более быстрым), но с использованием случайного ключа получателя и помещается в начало шифрограммы.

Алгоритм RSA стал первым алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи. Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов. (Факторизацией натурального числа называется его разложение в произведение простых множителей. Дискретное логарифмирование - задача обращения функции g^x. Наиболее часто задачу дискретного логарифмирования рассматривают в мультипликативной группе кольца вычетов или конечного поля, а также в группе точек эллиптической кривой над конечным полем. Эффективные алгоритмы для решения задачи дискретного логарифмирования в общем случае неизвестны. Для заданных g и a решение x уравнения g^x = a называется дискретным логарифмом элемента a по основанию g).

Первый этап любого асимметричного алгоритма - создание пары ключей:

1. Выбираются два больших простых числа р и q (простым называется число, делящееся на

единицу и на само себя).

2. Вычисляется n= (p  q).

3. Выбирается произвольное число e (e < n) такое, что наибольший общий делитель НОД (e,

(p-1)  (q-1)) = 1, т. е. должно быть взаимно простым с числом (p-1)  (q-1).

4. Методом Евклида решается в целых числах уравнение e  d + (p-1)  (q-1)  y = 1. Здесь

неизвестными являются переменные d и y - метод Евклида как раз и находит множество

пар (d, y), каждая из которых является решением уравнения в целых числах.

5. Пара чисел (e, n) - публикуется как открытый ключ. Число d хранится в строжайшем

секрете - это и есть закрытый ключ, который позволит читать все послания, зашифрованные с помощью пары ключей (e, n).

Второй этап - собственно шифрование с помощью открытого ключа.

1. Отправитель разбивает свое сообщение на блоки, равные k = [log₂ (n)] , где квадратные

скобки - взятие целой части от дробного числа. Подобный блок может быть интерпретирован как число из диапазона (0 : 2^k – 1).

2. Для каждого такого числа (назовем его m_i) вычисляется выражение c_i = ((m_i)^e) mod n. Блоки c_i и есть зашифрованное сообщение. Их можно без опасения передавать по открытому каналу, поскольку операция возведения в степень по модулю простого числа является трудноразрешимой математической задачей.

Третий этап - дешифрование послания с помощью секретного ключа. Частный случай теоремы Эйлера утверждает, что если число n может быть представлено в виде произведения двух простых чисел p и q, то для любого х имеет место равенство:

(х^{(р-1)  (q-1)}) mod n = 1.

Возведем обе ее части в степень (-y): ((х^{(-y)  (р-1)  (q-1)}) mod n = 1^(-y) = x. После умножения обеих частей равенства на х получим:

(х^{(-y)  (р-1)  (q-1)}) mod n = 1  = х

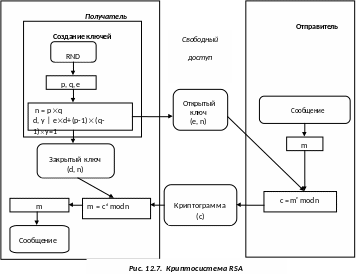
Алгоритм: Взять открытый ключ стороны Взять открытый текст Передать шифрованное сообщение:

Алгоритм: Принять зашифрованное сообщение Применить свой секретный ключ для расшифровки сообщения:

Пример1. Пусть р = 5, а q = 11, тогда значение n = 55. В качестве открытого ключа е выберем число 7, таким образом, весь открытый ключ имеет вид (е=7, n=55).

Вычислим закрытый ключ d: уравнение e  d + (p-1)  (q-1)  y = 1 приобретает вид

7  d + 40  y = 1 и имеет в целых числах решение d = 23, y = - 4. Таким образом, закрытым ключом являются числа (23, 55).

Пусть произвольный отправитель хочет передать абоненту комбинацию бит 100111₂ , ее числовой эквивалент 39₁₀ . Возводим 39 в степень открытого ключа е = 7 по модулю n = 55: (39⁷ mod 55) = 19. Число 19 является шифрограммой и передается по каналу связи. Получатель по приходу сообщения возводит его в степень d = 23: (19²³ mod 55) = 39.

Пример2.

Этап	Описание операции	Результат операции
Генерация ключей	Выбрать два простых числа
	Вычислить модуль
	Вычислить функцию Эйлера
	Выбрать открытую экспоненту
	Вычислить секретную экспоненту
	Опубликовать открытый ключ
	Сохранить секретный ключ
Шифрование	Выбрать текст для зашифровки
	Вычислить шифротекст
Расшифрование	Вычислить исходное сообщение

Алгоритм RSA намного медленнее чем DES и другие алгоритмы блочного шифрования. Программная реализация DES работает быстрее, по крайней мере, в 100 раз и от 1000 до 10 000 - в аппаратной реализации.

На 2009 год система шифрования на основе RSA считается надёжной, начиная с размера в 1024 бита.

Удалось успешно вычислить данные, зашифрованные при помощи криптографического ключа стандарта RSA длиной 768 бит. Причём от шифрования ключом длиной в 1024 бит стоит отказаться в ближайшие три-четыре года.

Вычисление значений ключа осуществлялось общим методом решета числового поля.

На первый шаг (выбор пары полиномов степени 6 и 1) было потрачено около полугода вычислений на 80 процессорах, что составило около 3 % времени, потраченного на главный этап алгоритма (просеивание), который выполнялся на сотнях компьютеров в течение почти двух лет. Если интерполировать это время на работу одного процессора AMD Opteron 2.2ГГц с 2Гб памяти, то получилось бы порядка 1500 лет. Обработка данных после просеивания для следующего ресурсоёмкого шага (линейной алгебры) потребовалось несколько недель на малом количестве процессоров. Заключительный шаг после нахождения нетривиальных решений ОСЛУ занял не более 12 часов.

Решение ОСЛУ проводилось с помощью метода Видемана на нескольких раздельных кластерах и длилось чуть менее 4 месяцев. При этом размер разреженной матрицы составил 192 796 550 х 192 795 550 при наличии 27 795 115 920 ненулевых элементов (то есть в среднем 144 ненулевых элементов на строку). Для хранения матрицы на жёстком диске понадобилось около 105 гигабайт. В то же время понадобилось около 5 терабайт сжатых данных для построения данной матрицы.

В итоге группе удалось вычислить 232-цифровой ключ, открывающий доступ к зашифрованным данным. Исследователи уверены, что используя их метод факторизации, взломать 1024-битный RSA-ключ будет возможно в течение следующей декады.

Зная разложение модуля на произведение двух простых чисел, противник может легко найти секретную экспоненту и тем самым взломать RSA. Однако на сегодняшний день самый быстрый алгоритм факторизации - решето обобщённого числового поля (General Number Field Sieve), скорость которого для k-битного целого числа составляет

для некоторого ,

не позволяет разложить большое целое за приемлемое время.

Однонаправленные функции

Понятие однонаправленной функции является основным в криптографии с открытым ключом. К однонаправленным относят такие функции, которые достаточно легко вычислить, но значительно труднее обратить. То есть, при наличии х нетрудно определить f(x), однако, при условии знания только f(x) на нахождение соответствующего значения х уйдут миллионы лет вычислений.

(Аналог - разбитая стеклянная бутылка. Расколотить ее на мелкие осколки очень легко, однако попробуйте снова собрать целую бутылку из осколков).

Существует множество функций, которые все считают однонаправленными: их значения довольно эффективно вычисляются, однако обратить эти функции каким-либо простым методом не удается.

В криптографии спросом пользуются однонаправленные функции с лазейкой, которые представляют собой особую разновидность однонаправленных функций. Однонаправленную функцию с лазейкой по-прежнему трудно обратить, но только не зная секрета вычисления обратной к ней функции. То есть, при данном х легко найти f(x) и наоборот - трудно отыскать х, зная одно лишь значение f(x). Однако существует такая секретная информация (у), что если известны у и f(x), то вычислить х будет значительно проще.

Особый интерес представляют однонаправленные хеш-функции. Алгоритмы хеширования, реализуемые с помощью хеш-функций, позволяют преобразовывать строки переменной длины, называемые образами, в строки фиксированной длины, которые принято именовать хеш-значениями. Хеш-значение гораздо меньше любого из образов (контрольная сумма). Однако такая хеш-функция не является однонаправленной: нетрудно подобрать строку символов, суммирование которых по модулю 2 даст заранее заданное значение.

Коллизией хеш-функции H называется два различных входных блока данных x и y таких, что:

H(x) = H(y).

Коллизии существуют для большинства хеш-функций, но для «хороших» хеш-функций частота их возникновения близка к теоретическому минимуму. В некоторых частных случаях, когда множество различных входных данных конечно, можно задать инъективную хеш-функцию, по определению не имеющую коллизий. Однако, для хеш-функций, принимающих вход переменной длины и возвращающих хеш постоянной длины (MD5), коллизии обязаны существовать, поскольку хотя бы для одного значения хеш-функции соответствующее ему множество входных данных (полный прообраз) будет бесконечно - и любые два набора данных из этого множества образуют коллизию.

Пример: хеш-функция H(x) = xmod 19, определенную на множестве целых чисел. Её область значений состоит из 19 элементов (кольца вычетов по модулю 19), а область определения - бесконечна. Так как множество прообразов заведомо больше множества значений, коллизии обязаны существовать.

Построим коллизию для этой хеш-функции для входного значения 38, хеш-сумма которого равна нулю. Так как функция H(x) - периодическая с периодом 19, то для любого входного значения y, значение y+19 будет иметь ту же хеш-сумму, что и y. В частности, для входного значения 38 той же хеш-суммой будут обладать входные значения 57, 76, и т. д. Таким образом, пары входных значений (38,57), (38,76) образуют коллизии хеш-функции H(x).

Так как криптографические хеш-функции используются для подтверждения неизменности исходной информации, то возможность быстрого отыскания коллизии для них обычно равносильна дискредитации. Мерой криптостойкости хеш-функции считается вычислительная сложность нахождения коллизии. В идеале не должно существовать способа отыскания коллизий более быстрого, чем полный перебор. Если для некоторой хеш-функции находится способ получения коллизий существенно более быстрый, чем полный перебор, то эта хеш-функция перестает считаться криптостойкой и использоваться для передачи и хранения секретной информации.

Однонаправленная хеш-функция позволяет легко сгенерировать хеш-значение. Однако, зная только его, будет очень трудно подобрать соответствующий ему образ. Качественная однонаправленная хэш-функция чаше всего является непротиворечивой: весьма сложно получить два различных образа, для которых хеш-значение будет одним и тем же. По выходу такой хеш-функции невозможно сказать, что было подано на ее вход, а изменение даже одного бита образа приводит к смене в среднем половины бит соответствующего хеш-значения (лавинный эффект).

Многие современные алгоритмы шифрования с открытым ключом основаны на однонаправленности функции разложения на множители числа, являющегося произведением двух больших простых чисел. Эти алгоритмы также могут быть подвергнуты атаке, подобной методу тотального перебора, с одним лишь отличием: опробовать каждый ключ не потребуется, достаточно суметь разложить на множители большое число.

Разложение большого числа на множители - задача трудная. В середине 70-х годов считалось, что для разложения на множители числа из 125 цифр потребуются десятки квадрильонов лет. А всего два десятилетия спустя с помощью компьютеров, подключенных к сети Internet удалось разложить на множители число из 129 цифр. Этот прорыв стал возможен благодаря тому, что за прошедшие 20 лет были не только предложены новые методы разложения на множители больших чисел, но и возросла производительность используемых компьютеров.

Поэтому квалифицированный криптограф должен проявлять большую осторожность и осмотрительность, когда речь заходит о длине открытою ключа. Необходимо учитывать, насколько ценна засекречиваемая с его помощью информация и как долго она должна оставаться в тайне для посторонних.

Таблица 10.3. Рекомендуемая длина открытого ключа (в битах)

Год	Хакер	Крупная корпорация	Правительство
2005	1024	1280	1536
2010	1280	1536	2048
2015	1536	2048	2048

А почему, спрашивается, не взять 10000-битный ключ. Ведь тогда отпадут все вопросы, связанные со стойкостью асимметричного алгоритма шифрования с открытым ключом, основанном на разложении большого числа па множители. Но дело в том, что обеспечение достаточной стойкости шифра не является единственной заботой криптографа. Имеются дополнительные соображения, влияющие на выбор длины ключа, и среди них вопросы, связанные с практической реализуемостью алгоритма шифрования при выбранной длине ключа.

Для организации шифрованной связи часто используются криптографические алгоритмы с секретным и с открытым ключом. Такая криптосистема называется гибридной. Стойкость каждого из алгоритмов, входящих в состав гибридной криптосистемы, должна быть достаточной, чтобы успешно противостоять вскрытию.

В табл. 10.4 перечисляются пары длин ключей для симметричного и асимметричного криптографического алгоритма, при которых стойкость обоих алгоритмов против криптоаналитической атаки методом тотального перебора приблизительно одинакова.

Таблица 10.4. Длины ключей для симметричного и асимметричного алгоритмов шифрования с одинаковой стойкостью против криптоаналитической атаки методом тотального перебора.

Длина ключа для симметричного алгоритма	Длина ключа для асимметричного алгоритма
56	384
64	512
128	2304