Часть 4. Парето – эффективность.

Задание:

Для каждой из биматричных игр, задания предыдущей части найти графическим путем Парето – множество решений, отметив здесь же решения, соответствующие равновесию по Нэшу.

Задача №1		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	( ); (-54)	( ); ( )
	2-я стратегия	(11); ( )	(27); (61)

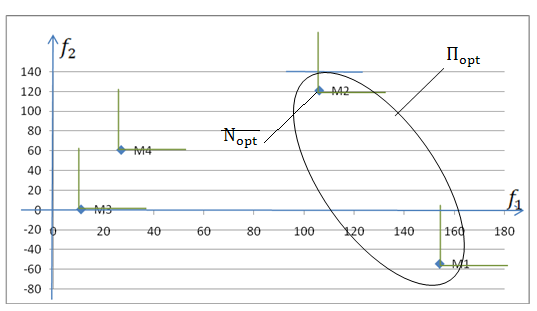
Задача №2		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	(119); (201)	(123); ( )
	2-я стратегия	( ); ( )	( ); (140)

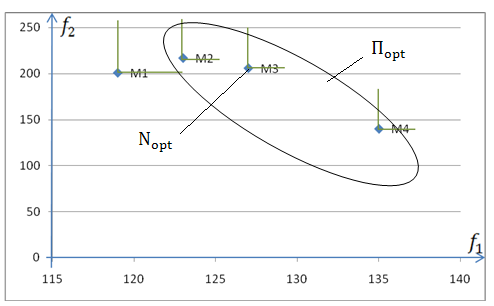
Задача №3		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	( ); (-36)	( ); ( )
	2-я стратегия	(27); ( )	(9); (-60)

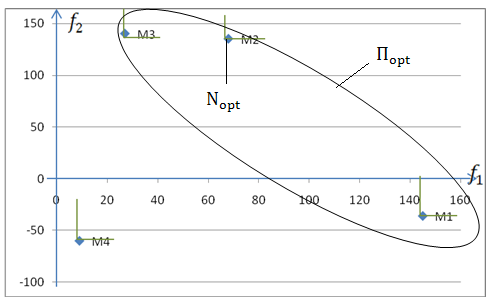
Задача №4		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	(-37); (51)	( ); ( )
	2-я стратегия	( ); ( )	(53); (91)

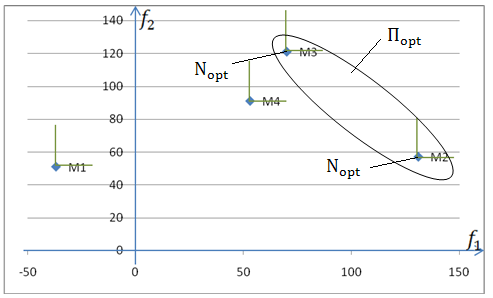
Задача №5		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	( ); ( )	( ); (-19)
	2-я стратегия	(52); ( )	(1); (35)

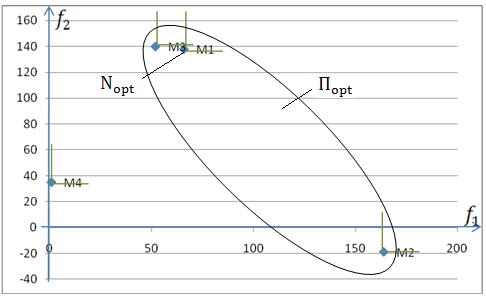
Задача №6		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	(12); (35)	( ); ( )
	2-я стратегия	( ); ( )	(-49); (46)

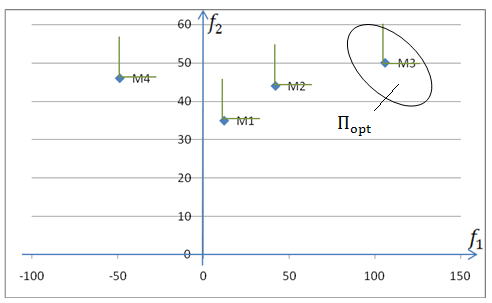
Задача №7		Игрок P2
		1-я стратегия	2-я стратегия
Игрок P1	1-я стратегия	(48); ( )	(-11); (120)
	2-я стратегия	( ); ( )	( ); (168)

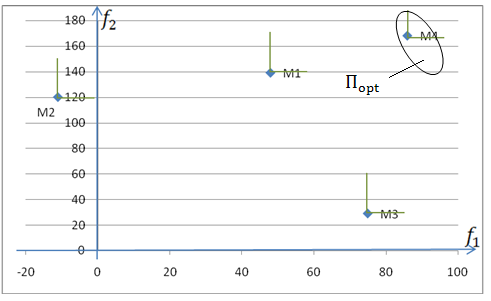
Часть 5. Последовательные игры.

Задание:

1. Представить графическую интерпретацию 4-х ходовой последовательной игры в виде единого графа, построенного из приведенных графов парных ходов.

2. Найти оптимальное решение для «разумного» поведения игроков, записав решение в виде

,

где ψ₁;ψ_{2 –} функции выбора стратегий в 1-й и 2-й двухходовках,

i, j, m, n – номера стратегий 1-го и 2-го игроков в 1-й и 2-й двухходовках,

a, b – результат 1-й двухходовки, c, d – текущий результат 2-й двухходовки.

А, В – итоговый результат 4-ч ходов игроков Р1 и Р2.

3. Найти наилучшие сценарии и их результаты для каждого из игроков Р1 и Р2

4. Найти наихудшие сценарии и их результаты для каждого из игроков Р1 и Р2

Найти агрессивно-нелогичные ходы обоих игроков позволяющие им влиять на решение противника в своих интересах, добиваясь «разумного» поведения противника.

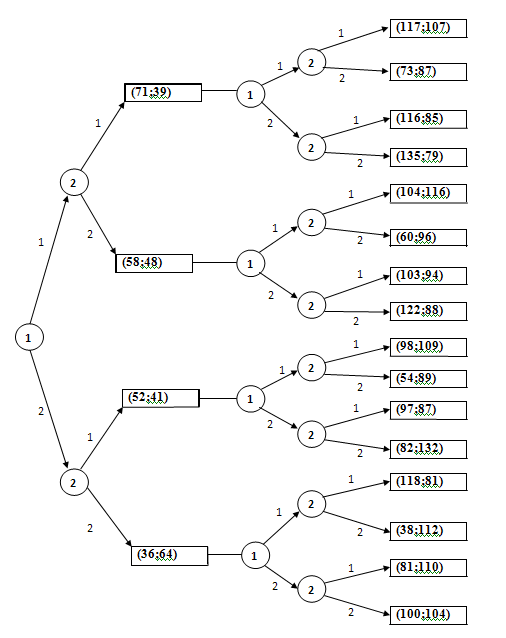
2) f_opt (ψ₁; ψ₂) = f_opt((1;2);(2;1)) = (f₁(1;2);f₂(2;1)) = ((58;48);(45;46)) = (103;94).

1-ый ход: игрок Р1 выбирает стратегию 1, т.к. стремится к максимально возможному выигрышу (135).

2-ой ход: игрок Р2 выбирает стратегию 2, т.к. стремится к максимально возможному выигрышу из оставшихся вариантов (116), он избежит своего наименьшего варианта (79), также лишит игрока Р1 возможности получить максимально возможную прибыль (135).

3-ий ход: игрок Р1 выбирает стратегию 2, т.к. стремится к максимально возможному выигрышу из оставшихся вариантов (122), он избежит наименьшего варианта из 4-х возможных.

4-ый ход: игрок Р2 выбирает стратегию 1, т.к. стремится получить наибольшую прибыль (94).

3) f_{max P1} = f ((1;1)(2;2)) = (135;79)

f_{max P2} = f ((2;2)(1;1)) = (82;132).

4) f_{min P1} = f ((2;2)(1;2)) = (38;112)

F_{min P2} = f ((1;1)(2;2)) = (135;79).

5) У игрока Р1 нет агрессивно-нелогичных ходов.

Игрок Р2: (1;1;1;2) вместо разумного поведения (1;1;1;1);

(1;2;1;2) вместо разумного поведения(1;2;1;1);

(2;1;1;2) вместо разумного поведения(2;1;1;1);

(2;2;1;2) вместо разумного поведения (2;2;1;1).