Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ
УНИВЕРСИТЕТ им. ак. С.П.КОРОЛЕВА
Курсовая работа по курсу «Теория Игр»
Выполнила студентка 731 гр.,
Ю.Н.Чернышова
Проверил В.М. Дуплякин
Самара 2010
Часть 1. Матричные игры с нулевой суммой 2х2
Задание:
Для заданных трех платежных матриц найти нижнюю и верхнюю цену игры.
В каждой из рассмотренных игр установить возможность решения в чистых стратегиях.
Представить графическую иллюстрацию оптимальных решений для обоих игроков.
Найти оптимальные решения в каждой игре расчетным путем.
Игра №1
59 |
71 |
73 |
52 |
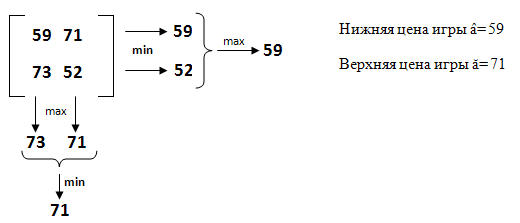Так
как â<ă,то из этого следует,что данная
игра не имеет решения в чистых
стратегиях.Однако по теореме Дж. Фон
Неймана решение матричной игры есть
всегда,и в данном случае его следует
искать смешанных стратегиях.
Оптимальное решение для игрока Р1:
P1:
ν=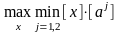
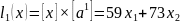
Выразим
вторую координату через первую:
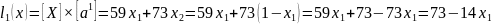
Оптимальных решений на отрезке [0;1] нет. Найдем решения по графику. Для графического отображения полученных результатов найдем крайние значения скалярных функций, подставив соответствующие значения аргументов, х1 = 0; х1 = 1.
Линии |
Аргументы |
|
x1=0 |
x1=1 |
|
l1(x1) |
73 |
59 |
l2(x1) |
52 |
71 |
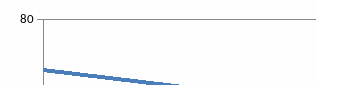
Приравнивая уравнения линии l1(x1), l2(x1), найдем координату точки их пересечения, которая представляет собой оптимальную вероятность выбора первой стратегии.
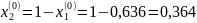
Данный результат точнее графического.
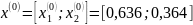
Оптимальное решение для игрока Р1:
ν=
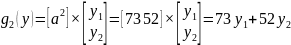
Выразим
вторую координату через первую
=
=
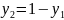
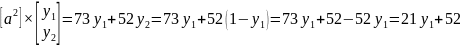
Оптимальных решений на отрезке [0;1] нет. Найдем решения по графику. Для графического отображения полученных результатов найдем крайние значения скалярных функций, подставив соответствующие значения аргументов, х1 = 0; х1 = 1.
Линии |
Аргументы |
|
y1=0 |
y1=1 |
|
g1(y1) |
71 |
59 |
g2(y1) |
52 |
73 |
Приравнивая уравнения линии g1(y1), g2(y1), найдем оптимальное относительное содержание второй стратегии игрока Р2.
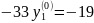
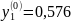
Данный результат точнее графического.
=
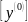Игра №2
68 |
65 |
43 |
93 |
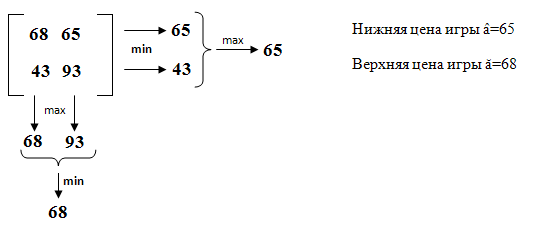
Так как â<ă,то из этого следует,что данная игра не имеет решения в чистых стратегиях.Однако по теореме Дж. Фон Неймана решение матричной игры есть всегда,и в данном случае его следует искать смешанных стратегиях.
Оптимальное решение для игрока Р1:
P1:
ν=
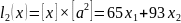
Выразим вторую координату через первую:
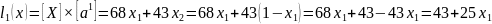
Оптимальных решений на отрезке [0;1] нет. Найдем решения по графику. Для графического отображения полученных результатов найдем крайние значения скалярных функций, подставив соответствующие значения аргументов, х1 = 0; х1 = 1.
Линии |
Аргументы |
|
x1=0 |
x1=1 |
|
l1(x1) |
43 |
68 |
l2(x1) |
93 |
65 |
Приравнивая уравнения линии l1(x1), l2(x1), найдем координату точки их пересечения, которая представляет собой оптимальную вероятность выбора первой стратегии.
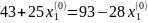
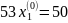
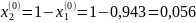
Данный результат точнее графического.
Оптимальное решение для игрока P2:
ν=
Выразим вторую координату через первую:
=
=
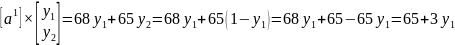
Оптимальных решений на отрезке [0;1] нет. Найдем решения по графику. Для графического отображения полученных результатов найдем крайние значения скалярных функций, подставив соответствующие значения аргументов, х1 = 0; х1 = 1.
Линии |
Аргументы |
|
y1=0 |
y1=1 |
|
g1(y1) |
65 |
68 |
g2(y1) |
93 |
43 |
Приравнивая уравнения линии g1(y1), g2(y1), найдем оптимальное относительное содержание второй стратегии игрока Р2.
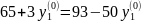
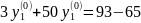
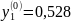
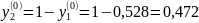
Данный результат точнее графического.
=
Игра №3
44 |
46 |
32 |
39 |
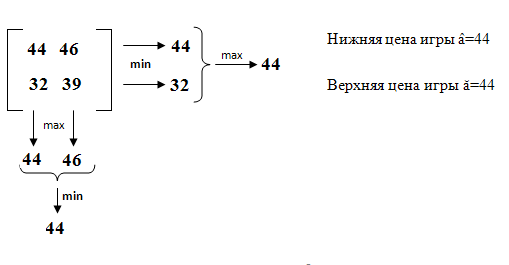
Так как â=ă,значит есть решения в чистых стратегиях.
Графической иллюстрацией нахождения оптимальных решений в чистых стратегиях является изображение седловой точки