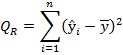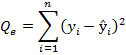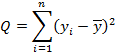- •1. Эконометрика как наука. Предмет эконометрики.
- •2. Критерии и принципы эконометрики.
- •3. Цели и задачи эконометрики.
- •4. Введение в эконометрическое моделирование
- •5. Основные этапы эконометрического моделирования.
- •6. Функциональная, стохастическая и корреляционная зависимости.
- •7. Парная линейная регрессия.
- •8. Коэффициент корреляции.
- •9. Основные предположения регрессионного анализа.
- •10. Оценка значимости уравнения регрессии.
- •11. Коэффициент детерминации.
- •12. Множественный регрессионный анализ.
9. Основные предположения регрессионного анализа.
В
регрессионном анализе зависимость Y
от
X может
быть представлена в виде модельного
уравнения регрессии
(3.1). В силу воздействия неучтенных
случайных факторов и причин отдельные
наблюдения переменной У
будут в большей или меньшей мере
отклоняться от функции регрессии 𝜑(х).
В
этом случае уравнение
взаимосвязи двух переменных (парная
регрессионная модель) может
быть представлено в виде:![]() ,
где ℰ
— случайная
переменная (случайный член), характеризующая
отклонение от функции регрессии. Эту
переменную будем называть возмущающей
или
просто возмущением
(либо
ошибкой).
Таким
образом, в регрессионной модели зависимая
переменная Y есть некоторая функция
𝜑(X)
с точностью до случайного возмущения
ℰ.
Рассмотрим
линейный
регрессионный анализ, для
которого функции 𝜑(X)
линейна
относительно оцениваемых параметров:
,
где ℰ
— случайная
переменная (случайный член), характеризующая
отклонение от функции регрессии. Эту
переменную будем называть возмущающей
или
просто возмущением
(либо
ошибкой).
Таким
образом, в регрессионной модели зависимая
переменная Y есть некоторая функция
𝜑(X)
с точностью до случайного возмущения
ℰ.
Рассмотрим
линейный
регрессионный анализ, для
которого функции 𝜑(X)
линейна
относительно оцениваемых параметров:
![]() .
(3.21).
Предположим,
что для оценки параметров линейной
функции регрессии (3.21)
взята
выборка, содержащая п
пар
значений переменных (xi,yi),
где i=1,2,...,
п.
В
этом случае линейная
парная регрессионная модель имеет
вид:
.
(3.21).
Предположим,
что для оценки параметров линейной
функции регрессии (3.21)
взята
выборка, содержащая п
пар
значений переменных (xi,yi),
где i=1,2,...,
п.
В
этом случае линейная
парная регрессионная модель имеет
вид:![]() .
(3.22).
.
(3.22).
Основные предпосылки регрессионного анализа.
1. В модели (3.22) возмущение ℰi (или зависимая переменная уi) есть величина случайная, а объясняющая переменная хi — величина mнеслучайная.
2.
Математическое
ожидание возмущения ℰi
равно
нулю: M(ℰi)=0
(3.23)
(или математическое ожидание зависимой
переменной yi
равно
линейной функции регрессии: ![]() .
.
3.
Дисперсия
возмущения ℰi
(или зависимой переменной уi
)постоянна для любого i:
![]() (3.24)
(или
— условие
гомоскедастичности
или
равноизменчивости
возмущения
(зависимой переменной)).
(3.24)
(или
— условие
гомоскедастичности
или
равноизменчивости
возмущения
(зависимой переменной)).
4. Возмущения ℰi и ℰj (или переменные yi и yj) не коррелированы M(ℰi ℰj)=0(i≠j). (3.25)
5. Возмущение ℰi (или зависимая переменная уi) есть нормально распределенная случайная величина. В этом случае модель (3.22) называется классической нормальной линейной регрессионной моделью.
Для получения уравненртя регрессии достаточно предпосылок 1—4. Требование выполнения предпосылки 5 (т. е. рассмотрение «нормальной регрессии») необходимо для оценки точности уравнения регрессии и его параметров.
Оценкой модели (3.22) по выборке является уравнение регрессии ŷ = b0 + b1 (3.3). Параметры этого уравнения b0 и b1 определяются на основе метода наименьших квадратов.
Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (3.22) определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии 𝜎2. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.
10. Оценка значимости уравнения регрессии.
Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.
Основная идея дисперсионного анализа: Q=QR+Qe, (3.41) где Q – общая сумма квадратов отклонений зависимой переменной
от средней , QR и Qe — соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов
Схема дисперсионного анализа :
Компоненты дисперсии |
Сумма квадратов |
Число степеней свободы |
Средние квадраты |
Регрессия |
|
m-1 |
|
Остаточная |
|
n-m |
|
Общая |
|
n-1 |
|
Средние квадраты SR2 и S2 представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессий или объясняющей переменной X и воздействием неучтенных случайных факторов и ошибок; т — число оцениваемых параметров уравнения регрессии; п — число наблюдений.