3. Вероятности перехода за несколько шагов
Мы обозначим через
вероятность перехода из
в
ровно за
шагов. Иначе говоря
есть условная вероятность попадания в
на
-м
шаге при условии, что начальным состоянием.
Было
;
она равна сумме вероятностей всех путей
длины
,
начинающихся в
и оканчивающихся в
.
В частности,
и
(3.1)
По индукции мы получаем общую рекуррентную формулу
(3.2)
дальнейшая индукция по
приводит к основному тождеству
(3.3)
(которое является частным случаем
уравнения Колмогорова-Чепмена). Оно
отражает тот простой факт, что первые
шагов приводят из
в некоторое промежуточное состояние
и что вероятность последующего перехода
из
в
не зависит от того, каким образом было
достигнуто
.
Так же как и в случае
,
образовавших матрицу
,
мы расположим
в матрицу, которую обозначим
.
Тогда (3.2) утверждает, что для того, чтобы
получит элемент
матрицы
,
мы должны умножить элементы
-й
строки
на соответствующие элементы
-го
столбца
и сложить полученные произведения. Эта
операция называется умножением матриц
и
и выражается символически равенством
.
Данное определение позволяет назвать
-й
степенью
;
уравнение (3.3) выражает известный закон
.
Для того чтобы (3.3) было справедливо для
всех
,
мы определим
,
положив
и
при
,
что вполне естественно.
Примеры. а) Независимые испытания.
Обычно бывает трудно получить явные
выражения для вероятностей перехода
за несколько шагов, однако, к счастью
они не представляют особого интереса.
Как важное, хотя и тривиальное исключение,
мы отметим частный случай независимых
испытаний. Этот случай имеет место
тогда, когда все строки
тождественно совпадают с данным
распределением вероятностей, и ясно
без вычислений, чт о отсюда следует
равенство
при всех
.
б) Серии успехов. В примере д) (серии успехов) легко видеть (либо из рекуррентной формулы (3.2), либо из самого определения процесса), что
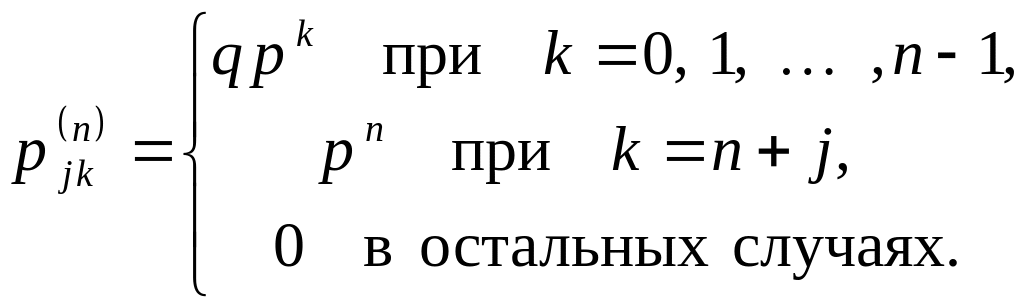
В этом случае ясно, что
сходится к матрице, такой, что все
элементы в ее столбце с номером
равны
.
Безусловные вероятности
Пусть снова
означает вероятность состояния
в начальном (нулевом) испытании. Тогда
(безусловная) вероятность попадания в
на
-м
шаге равна
. (3.4)
Обычно мы считаем, что процесс начинается
из фиксированного состояния
,
т.е. полагаем
.
В этом случае
.
Интуитивно мы чувствуем, что влияние
начального состояния должно постепенно
ослабевать, так как при больших
распределение (3.4) должно быть почти
независимым от начального распределения
.
Так оно и будет, если (как в последнем
примере)
сходится к независящему от
пределу, т.е. если
сходится к матрице с одинаковыми
строками. Мы видим, что обычно это
действительно так, хотя нам и придется
еще принимать в расчет досадные
исключения, обусловленные периодичностью.