Цепи маркова

1. Определение

Рассмотрим независимые испытания, которые можно описать следующим образом. Задано множество возможных исходов (в конечном или бесконечном числе), и каждому из них соотнесена некоторая вероятность ; вероятности последовательностей исходов определяются по правилу умножения: . В теории цепей Маркова мы рассматриваем простейшее обобщение этой схемы, которое состоит в том, что для любого испытания допускается зависимость его от непосредственно предшествующего ему испытания (и только от него). С исходом не связана более фиксированная вероятность , но зато каждой паре теперь соответствует условная вероятность ; при условии, что появился в некотором испытании, вероятность появления в следующем испытании равна . Помимо нам должны быть заданы вероятности исходов в начальном испытании. Чтобы имели приписанный им смысл, вероятности последовательностей исходов, соответствующих двум, трем или четырем испытаниям, должны быть определены равенствами

и вообще

(1.1)

Здесь начальному испытанию присвоен номер нуль, так, что испытание номер один является вторым.

Пример. Случайные блуждания. Случайное блуждание на прямой является цепью Маркова, однако в этом случае возможные положения естественно представить в виде бесконечной в обе стороны последовательности … , –2, –1, 0, 1, 2, … . При таком порядке переходы будут возможны только между соседними положениями, т.е. , если . Чтобы воспользоваться нашими нынешними обозначениями, нам пришлось бы расположить целые числа в простую последовательность, скажем 0, 1, –1, 2, –2, … , и это привело бы к громоздким формулам для вероятностей . То же замечание справедливо и в отношении случайных блужданий в пространствах высшей размерности: для практических вычислений лучше обозначать точки значениями их координат, а для теоретических целей можно пользоваться символикой настоящей главы.

Определение. Последовательность испытаний с возможными исходами называется цепью Маркова, если вероятности последовательностей исходов определяются формулой (1.1) через распределение вероятностей для в начальном (или нулевом) испытании и через фиксированные условные вероятности появления при условии, что в предыдущем испытании появился .

Для приложений цепей Маркова удобнее несколько видоизмененная технология. Возможные исходы обычно называются возможными состояниями системы; вместо того, чтобы говорить, что -е испытание окончилось появлением , говорят, что -й шаг приводит к состоянию или что система попадает в на -м шаге. Наконец, называется вероятностью перехода из в . Как обычно, мы считаем, что испытания происходят через равные интервалы времени, так что номер шага служит временным параметром.

Вероятности перехода будут расположены в матрицу переходных вероятностей

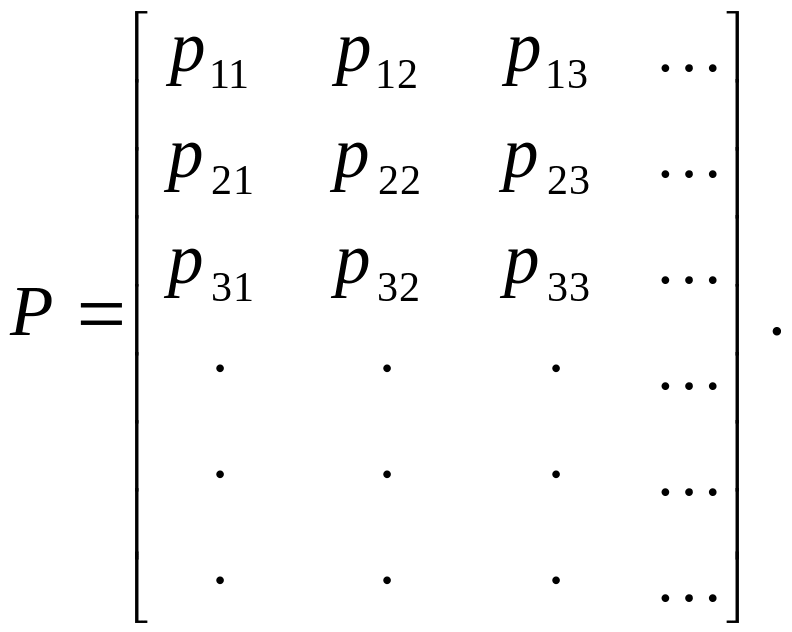(1.3)

где первый индекс означает номер строки, а второй – номер столбца. Ясно, что – квадратная матрица с неотрицательными элементами и единичными суммами по строкам. Такая матрица (конечная или бесконечная) называется стохастической матрицей. Любая стохастическая матрица может служить матрицей переходных вероятностей; вместе с нашим начальным распределением она полностью определяет цепь Маркова с состояниями .

В некоторых частных случаях бывает удобно нумеровать состояния, начиная с 0, а не с 1. Тогда к матрице следует добавить нулевые строку и столбец.