2.2. Проверим статистическую значимость параметров и уравнения множественной регрессии с надёжностью 0,95.
Проверка осуществляется по формуле.
, где rxy – коэффициент множественной корреляции.
Коэффициент множественной корреляции определяется по формуле:
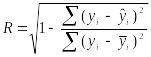
Расчётная таблица.
i |
yi |
xi1 |
xi2 |
yiп |
(yi -yiп) 2 |
(yi -yiср) 2 |
1 |
3658 |
3193,08 |
55,21 |
3664,08 |
36,96 |
1570021,53 |
2 |
3741,1 |
3236,02 |
60,08 |
3759,18 |
326,89 |
1368677,71 |
3 |
3791,7 |
3275,52 |
63,48 |
3832,31 |
1649,19 |
1252843,68 |
4 |
3906,9 |
3454,3 |
66,19 |
3994,80 |
7725,78 |
1008226,85 |
5 |
4207,6 |
3640,39 |
68,63 |
4158,87 |
2375,07 |
494778,594 |
6 |
4347,8 |
3821,1 |
70,99 |
4318,07 |
884,16 |
317199,872 |
7 |
4486,6 |
3981,3 |
72,72 |
4454,38 |
1037,92 |
180119,604 |
8 |
4582,5 |
4113,4 |
75,49 |
4584,65 |
4,60 |
107915,535 |
9 |
4784,1 |
4279,5 |
78,44 |
4741,35 |
1827,43 |
16104,879 |
10 |
4906,5 |
4393,7 |
81,86 |
4867,59 |
1513,98 |
20,295025 |
11 |
5014,2 |
4474,5 |
85,63 |
4974,85 |
1548,17 |
10649,208 |
12 |
5033 |
4466,6 |
88,91 |
5012,86 |
405,72 |
14882,78 |
13 |
5189,3 |
4594,5 |
91,62 |
5139,35 |
2494,87 |
77448,107 |
14 |
5261,3 |
4748,9 |
93,81 |
5277,68 |
268,31 |
122706,587 |
15 |
5397,2 |
4928,1 |
95,7 |
5429,57 |
1047,51 |
236385,578 |
16 |
5539,1 |
5075,6 |
97,9 |
5563,15 |
578,20 |
394503,329 |
17 |
5677,7 |
5237,5 |
100 |
5705,58 |
777,51 |
587821,223 |
18 |
5854,5 |
5423,9 |
101,94 |
5863,23 |
76,16 |
890182,815 |
19 |
6331 |
5978,8 |
104,85 |
6294,44 |
1336,75 |
2016385,8 |
20 |
6510 |
6294,6 |
107,38 |
6551,46 |
1718,96 |
2556785,01 |
Сумма |
98220,1 |
88611,3 |
1660,83 |
98220,1 |
27634,14 |
13223658,99 |
=
Коэффициент детерминации равен: 0,999, следовательно, множественная регрессия объясняет 99,9% колебаний значений y. Это свидетельствует о значительном суммарном влиянии независимых переменных x1 и x2 на y.
Проверим статистическую значимость коэффициента множественной корреляции.
В нашем случае.
Условие выполняется, следовательно, коэффициент множественной корреляции существенно отличен от нуля.
Проверим уравнение регрессии на значимость.
В нашем случае.
для
зависимости у от х1
и x2.
Табличное значение Fт=4,35 (для α=0,05)
Так как в нашем случае FФ больше Fт, то признаём статистическую значимость уравнения регрессии.