Задание 2
Множественная линейная модель. Имеются сведения о величине располагаемого личного дохода и различных потребительских расходах населения США с 1980 по 1999 годы (в ценах 1996 года). Оцените зависимость потребительских расходов (переменная Y) от личного располагаемого дохода (переменная Х1) и индекса соответствующей цены (ИОЦ) (переменная Х2) с помощью модели множественной линейной регрессии. Проверить значимость параметров регрессии и соответствие модели выборочным данным. Построить доверительные интервалы для коэффициентов регрессии при 5% уровне значимости.
С помощью построенной модели найти точечный и интервальный прогнозы на 2000 год при 5% уровне значимости, определить отклонение точечного прогноза от реального значения в %.
Годы |
Личные доходы |
Личные расходы |
ИОЦ на общие расходы |
1980 |
3658 |
3193,08 |
55,21 |
1981 |
3741,1 |
3236,02 |
60,08 |
1982 |
3791,7 |
3275,52 |
63,48 |
1983 |
3906,9 |
3454,3 |
66,19 |
1984 |
4207,6 |
3640,39 |
68,63 |
1985 |
4347,8 |
3821,1 |
70,99 |
1986 |
4486,6 |
3981,3 |
72,72 |
1987 |
4582,5 |
4113,4 |
75,49 |
1988 |
4784,1 |
4279,5 |
78,44 |
1989 |
4906,5 |
4393,7 |
81,86 |
1990 |
5014,2 |
4474,5 |
85,63 |
1991 |
5033 |
4466,6 |
88,91 |
1992 |
5189,3 |
4594,5 |
91,62 |
1993 |
5261,3 |
4748,9 |
93,81 |
1994 |
5397,2 |
4928,1 |
95,7 |
1995 |
5539,1 |
5075,6 |
97,9 |
1996 |
5677,7 |
5237,5 |
100 |
1997 |
5854,5 |
5423,9 |
101,94 |
1999 |
6331 |
5978,8 |
104,85 |
2000 |
6510 |
6294,6 |
107,38 |
Решение
2.1. По методу наименьших квадратов находим оценки коэффициентов множественной линейной регрессионной модели
Система нормальный уравнений имеет вид.
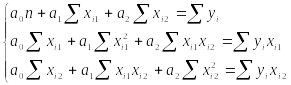
Находим численные значения оценок в данной задаче. Обозначим:
;
;
;
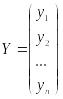
Тогда
Сведём расчётные данные в таблицу.
i |
yi |
xi1 |
xi2 |
xi12 |
xi22 |
xi1* xi2 |
yi* xi1 |
yi* xi2 |
1 |
3658 |
3193,08 |
55,21 |
10195759,9 |
3048,144 |
176289,947 |
11680286,6 |
201958,2 |
2 |
3741,1 |
3236,02 |
60,08 |
10471825,4 |
3609,606 |
194420,082 |
12106274,4 |
224765,3 |
3 |
3791,7 |
3275,52 |
63,48 |
10729031,3 |
4029,71 |
207930,01 |
12419789,2 |
240697,1 |
4 |
3906,9 |
3454,3 |
66,19 |
11932188,5 |
4381,116 |
228640,117 |
13495604,7 |
258597,7 |
5 |
4207,6 |
3640,39 |
68,63 |
13252439,4 |
4710,077 |
249839,966 |
15317305 |
288767,6 |
6 |
4347,8 |
3821,1 |
70,99 |
14600805,2 |
5039,58 |
271259,889 |
16613378,6 |
308650,3 |
7 |
4486,6 |
3981,3 |
72,72 |
15850749,7 |
5288,198 |
289520,136 |
17862500,6 |
326265,6 |
8 |
4582,5 |
4113,4 |
75,49 |
16920059,6 |
5698,74 |
310520,566 |
18849655,5 |
345932,9 |
9 |
4784,1 |
4279,5 |
78,44 |
18314120,3 |
6152,834 |
335683,98 |
20473556 |
375264,8 |
10 |
4906,5 |
4393,7 |
81,86 |
19304599,7 |
6701,06 |
359668,282 |
21557689,1 |
401646,1 |
11 |
5014,2 |
4474,5 |
85,63 |
20021150,3 |
7332,497 |
383151,435 |
22436037,9 |
429365,9 |
12 |
5033 |
4466,6 |
88,91 |
19950515,6 |
7904,988 |
397125,406 |
22480397,8 |
447484 |
13 |
5189,3 |
4594,5 |
91,62 |
21109430,3 |
8394,224 |
420948,09 |
23842238,9 |
475443,7 |
14 |
5261,3 |
4748,9 |
93,81 |
22552051,2 |
8800,316 |
445494,309 |
24985387,6 |
493562,6 |
15 |
5397,2 |
4928,1 |
95,7 |
24286169,6 |
9158,49 |
471619,17 |
26597941,3 |
516512 |
16 |
5539,1 |
5075,6 |
97,9 |
25761715,4 |
9584,41 |
496901,24 |
28114256 |
542277,9 |
17 |
5677,7 |
5237,5 |
100 |
27431406,3 |
10000 |
523750 |
29736953,8 |
567770 |
18 |
5854,5 |
5423,9 |
101,94 |
29418691,2 |
10391,76 |
552912,366 |
31754222,6 |
596807,7 |
19 |
6331 |
5978,8 |
104,85 |
35746049,4 |
10993,52 |
626877,18 |
37851782,8 |
663805,4 |
20 |
6510 |
6294,6 |
107,38 |
39621989,2 |
11530,46 |
675914,148 |
40977846 |
699043,8 |
Сумма |
98220,1 |
88611,3 |
1660,83 |
407470747 |
142749,7 |
7618466,32 |
449153104 |
8404619 |
В нашем случае.
Множественная линейная регрессионная модель
имеет
вид:
