2. Методы анализа количественного влияния факторов на изменение результативного показателя (детерминированного факторного анализа).

Все приемы и способы детерминированного факторного анализа предполагают количественное определение влияния каждого фактора приемами элиминирования (устранения).

Основными приемами (способами) детерминированного анализа являются:

• цепная подстановка (на ПЗ),

• изолированные подстановки,

• абсолютные разницы,

• индексные методы (на ПЗ),

• интегральный метод (на ПЗ),

• балансовый метод.

Метод цепных подстановок

Этот метод заключается в получении ряда промежуточных значений обобщающего (результативного) показателя путем последовательной замены базисных значений факторов на фактические. Разность двух промежуточных значений обобщающего показателя в цепи подстановок равна изменению обобщающего показателя, вызванного изменением соответствующего фактора.

Математическое описание метода:

– формула факторной зависимости, например,

- базисное значение обобщающего показателя;

- промежуточное значение;

- промежуточное значение;

- промежуточное значение;

- фактическое значение обобщающего показателя.

Общее абсолютное значение обобщающего показателя определяется по формуле:

Общее отклонение обобщающего показателя раскладывается на факторы:

• за счет изменения фактора «а»

• за счет изменения фактора “b”

• за счет изменения фактора “c”

• за счет изменения фактора “d”

Баланс факторов:

Преимущества метода: небольшая трудоемкость, легкая запоминаемость.

Недостатки: результаты расчетов зависят от последовательности замены факторов, активная роль в изменении обобщающего показателя необоснованно часто приписывается влиянию изменения качественного фактора.

Метод абсолютных разниц

Метод абсолютных разниц заключается в расчете размера влияния факторов за один прием.

Математическое описание метода:

– формула факторной зависимости

Баланс факторов:

Преимущества метода: небольшая трудоемкость, легкая запоминаемость.

Недостатки: рассчитывается влияние сначала количественных, а затем качественных факторов.

Метод изолированных подстановок

Метод изолированных подстановок позволяет рассчитывать влияние факторов независимо от того, являются ли они качественными или количественными.

Однако этот метод увеличивает трудоемкость расчетов, так как возникает неразложенный или нераспределенный остаток (НО), который необходимо распределить пропорционально между всеми факторами.

Существует 2 варианта изолированных подстановок.

Первый вариант – основан на принципе цепных подстановок

Распределяем НО между i-тыми факторами по формуле:

, где ,

Баланс факторов:

Второй вариант – основан на принципе абсолютных разниц

Далее как в первом варианте.

Индексные методы

Индексные методы основаны на использовании статистических индексов изменения показателей факторов и обобщающего показателя.

Существует несколько вариантов использования индексных методов:

1. индексный статистический имеет строгие ограничения в количестве факторов (2), поэтому в аналитических расчетах самостоятельно используется редко;

2. индексный метод Тихоновой;

3. индексный классический предусматривает расчет влияния факторов в 2 этапа:

Первый этап – рассчитываем приращение индекса обобщающего показателя за счет i-ого фактора по следующей формуле:

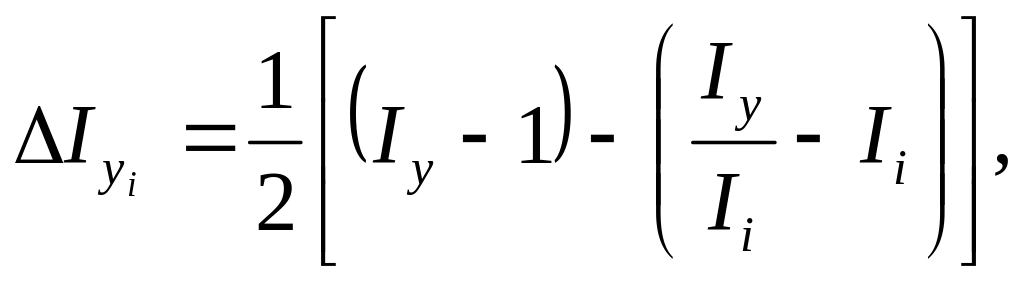
где I_y – индекс изменения обобщающего показателя,

I_i – индекс изменения i-ого фактора.

Второй этап – определяем абсолютное значение влияния i-ого фактора на обобщающий показатель по формуле:

.

Интегральный метод

Интегральный метод обеспечивает общий подход к решению задач самого разного вида независимо от количества элементов, входящих в факторную модель, и формы связи между ними.

Существует набор формул расчета элементов структуры мультипликативных и кратных факторных моделей, которые были выведены в результате процесса интегрирования.

Чаще всего используются следующие виды факторных систем:

1. 

- влияние фактора Х на функцию

- влияние фактора Y на функцию

2.

3.

- остаточный метод

4. 

Везде должен соблюдаться баланс факторов.