Точность вычисления площади аналитическим способом

Продифференцировав выражение площади треугольника и перейдя к средним квадратическим погрешностям, будем иметь

. Такую же формулу можно получить для площади прямоугольника, параллелограмма и трапеции.

Для трапеции, если измерены два основания и высота:

.

Будем считать, что измерение линий на местности производится с относительной погрешностью

, то .

Для четырехугольника, если его форма близка к квадрату

, или . Перейдя к средним квадратическим погрешностям получим

, или

(значение выражено в радианной мере).

Вычисление площади графическим способом

Графический метод определения площади подразумевает определение площади по элементам геометрических фигур, значения которых измерены по топографическому плану. К графическому методу относят также определение площади контуров, отображенных на топографическом плане с помощью специальных палеток.

Для определения площади участка местности (контура) отображённого на плане (карте) и имеющего прямолинейные границы, данный контур разбивают на примерно равные непересекающиеся между собой треугольники. В дальнейшем, по плану с помощью масштабной линейки и измерителя измеряют основание и высоту каждого треугольника.

Площадь треугольников вычисляют по известной формуле

Р=0,5аh ,

где Р-площадь треугольника,

а -основание треугольника,

h-высота треугольника.

Для контроля измерений площадь каждого треугольника измеряют дважды (по двум различным основаниям и высотам), при этом расхождение  площади треугольника в двух вариантах не должно превышать

 <= 0.04(M/10000)Р ,

где М - знаменатель масштаба плана. При этом целесообразно выполнить следующие рекомендации: 1) участок делить на фигуры возможно больших размеров; 2) площади полученных фигур определять по более простым формулам.

Если отображенный на плане контур имеет небольшие размеры, а границы его криволинейны, то его площадь измеряют с помощью квадратной или параллельной палетки.

Точность вычисление площадей графическим способом

Так как для треугольника ah=2P, а для остальных фигур a₁h₁=P, то

, а для прямоугольника, параллелограмма и трапеции

.

Если a=h, то для треугольника

.

Для трапеции, параллелограмма, прямоугольника при a₁=h₁

, т. е. площадь треугольника графическим способом вычисляется точнее, чем площади других фигур, и, следовательно площадь при разбивке участка на треугольники вычисляется точнее, чем при разбивке на прямоугольники, трапеции и др.

Так как погрешность измерения по плану 0,08 мм, то учитывая, что при разбивке фигуры на треугольники не всегда удается получить треугольника с равными основаниями и высотами, погрешность площади участка можно вычислить по формуле

, или для планов разных масштабов

, где М – знаменатель численного масштаба плана.

Механический способ определения площадей

Механический способ определения площади участка любой формы состоит в обводе ее на плане при помощи механического прибора – планиметра.

Полярный планиметр имеет два рычага: полюсный R₁ и обводной R (рис.). Один конец полюсного рычага - точка 0 - является полюсом планиметра, - на нем крепится игла; другой его конец шарнирно соединяется с обводным рычагом в точке b. На одном рычаге обводного рычага имеется счетное колесо K, которое располагается перпендикулярно рычагу, на другом конце рычага находится обводная точка f. Для механического счета числа оборотов счетного колеса имеется счетный механизм. Счетный барабан разделен на сто частей, и сбоку от него имеется верньер на одну десятую деления. Обводное колесо и счетный механизм помещаются на каретке, которую можно перемещать вдоль обводного рычага, изменяя тем самым его длину R = bf.

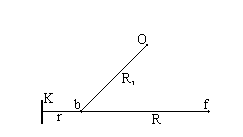
Измерение площади сводится к обводу по контуру участка на карте обводной точкой f; при этом вследствие трения о бумагу счетное колесо вращается. Берут отсчет по счетному механизму до обвода контура u₁ и после обвода - u₂. Площадь участка вычисляют по формуле:

P = p * ( u₂ - u₁ ),                 

где p - цена деления планиметра.

Внешний вид полярного планиметра изображен на рис.; на нем цифрами обозначены: 1 - основная каретка, 3 - полюсный рычаг, 4 - полюс, 6 - стеклянная пластинка с обводной точкой, 7 -обводной рычаг, 8 - шарнирное соединение, 9 - счетчик полных оборотов, 2, 10 - счетное колесо, 11 - верньер.

Делением планиметра называют 1:1000 часть окружности ободка счетного ролика. Деление планиметра, выраженное в линейной мере, как правило обозначают буквой «  ».

Один поворот циферблата соответствует 10 полным оборотам счетного ролика. Если учесть, что полный оборот счетного ролика соответствует 1000 делениям планиметра, то один оборот циферблата - 10000 делениям. Поэтому отсчет по циферблату состоит из четырёх цифр.

Если при измерении оборот обводного колеса составит одно деление планиметра, то пройденный им по топографическому плану путь равен :

Умножив деление планиметра на длину обводного рычага R (см.рис.) получим цену деления планиметра.

Цена деления планиметра представляет собой площадь, соответствующую одному делению планиметра.

Теоретическая цена деления планиметра определяется формулой

р= R,

где р - цена деления планиметра (мм² ),

 - деление планиметра ( мм),

18. длина обводного рычага, измеренная по шкале обводного рычага и выраженная в мм.

Цену деления планиметра, соотносят с площадью соответствующего прямоугольника на топографическом плане:

р₁ = RМ₁ ² ,

где М₁ -знаменатель масштаба плана.

Если цена деления планиметра при измерениях на плане масштаба М₁ составляет р₁ , то на другом плане, например масштаба M₂ , цена деления планиметра изменится и будет равна:

р₂ =  RМ₂ ² . Следовательно,

р₁ / р₂ = (М₁/ М₂ ) ².

Пример. На плане масштаба 1:10000 цена деления планиметра р₁ = 0,090000га. Вычислить цену деления этого же планиметра на плане масштаба 1:5000.

Решение.

р₂ = р₁ (М₂/ М₁ ) ² = 0,09(5000/10000)² =0,02250 га.

Цену деления планиметра можно изменить путем уменьшения (увеличения) длины обводного рычага.

Пример. Цена деления планиметра на плане масштаба М и длине обводного рычага R₁ (R₁= 163.3мм ) составляет 0,09522 га. Определить какой должна быть длина обводного рычага , при которой цена деления планиметра на плане этого же масштаба равна 0,1000 га.

Решение.

Цена деления планиметра при длине обводного рычага равной R₁ составит

р₁ =  R₁ М ² , а при длине обводного рычага равной R₂ ,будет равна

р₂ =  R₂ М ² .

Тогда,

(р₁ / р₂ ) = R₁ / R₂ .

Следовательно,

R₂ = R₁ (р₂ / р₁ ).

В соответствии с условием задачи примем р₁=0,09522 ,R₁ = 163.3мм , р₂=0,10000.

Тогда R₂ = 163,3 (0,10000 / 0,09522 )= 171,5 мм.

Вычисленное значение длины обводного рычага 171,5 мм устанавливается на линейке обводного рычага. Для этой цели, счетный механизм передвигают по обводному рычагу до тех пор, пока отсчет по линейке не будет совпадать с его вычисленным значение. После этого положение счетного механизма фиксируют зажимным винтом и подтверждают новую цену деления планиметра, путём обвода отображенной на плане фигуры известной площадью, например двух-трех квадратов координатной сетки.

В принципе, процесс измерения площади контура полярным планиметром сводится к следующему.

1) Обводной и полюсный рычаг с помощью шарниров соединяют между собой и с полюсом.

2) Полюс планиметра закрепляют на плане вне измеряемого контура таким образом, чтобы при обводе контура угол между полюсным и обводным рычагами (угол  , см.рис) был не менее 30 и не более 150, а его отклонения в обе стороны от величины 90 были бы примерно одинаковы. При установке полюса следует также предварительно проверить, чтобы в процессе обвода счетный ролик не выходил за край листа плана (или карты).

3) Перед началом измерений обводной индекс устанавливают в исходной точке контура и по циферблату берут отсчет u₁ , который называют «отсчет до обвода».

4. Удерживая обводной индекс на контуре его обводят по ходу часовой стрелки до начальной точки и по циферблату берут отсчет u₂.

5. Вычисляют площадь контура

Р (га) = р (u₂ - u₁ ),

где р - цена деления планиметра выраженная в гектарах.

При измерениях взаимное положение полярного и обводного рычага характеризуют одним из следующих понятий : «Полюс право» или «Полюс лево (ПЛ)»

Положение «Полюс право(ПП)» соответствует такому положению полюса планиметра, когда он расположен справа относительно обводного рычага (если смотреть на шарнирное соединении со стороны полюса). Аналогично определяется содержание термина «Полюс лево(ПЛ)».