8.4. Условия для идентификации

Приступать к оцениванию того или иного структурного урав­нения системы имеет смысл после того, как установлено его иден­тифицируемость.

Для установления идентифицируемости можно использовать инструментальные переменные (ИП).

В полностью определенной модели будет столько уравнений, сколько имеется эндогенных переменных.

Пусть D — число не включенных в уравнение, но присутст­вующих в системе экзогенных переменных, а Н — число включен­ных в уравнение эндогенных переменных.

Необходимое условие идентификации. Уравнение в струк­турной модели может быть идентифицировано, если число не вклю­ченных в него экзогенных переменных не меньше числа включен­ных в него объясняющих эндогенных переменных, т. е.

Н - 1 (порядковое условие).

Данное условие является необходимым, но не достаточным для идентификации.

В частности:

• если D= Н- 1, то уравнение точно идентифицируемо;

• если D> Н - 1, то уравнение сверхидентифицируемо',

• если D <Н- 1, то уравнение неидентифицируемо.

Достаточное условие идентификации. Уравнение идентифи­цируемо, если ранг матрицы, составленной из коэффициентов при переменных (эндогенных и экзогенных), отсутствующих в иссле­дуемом уравнении, не меньше N - 1, где N — число эндогенных пе­ременных системы.

Пример 8.10. Проверим на идентификацию каждое уравнение модели:

где у₁ — расходы на конечное потребление текущего года;

у₂ — валовые инвестиции в текущем году;

у₃ — расходы на заработную плату в текущем году;

у₄ — валовой доход за текущий год;

х₁ — валовой доход предыдущего года;

х₂ — государственные расходы текущего года;

— случайные ошибки.

В данной модели четыре эндогенные переменные (у₁ у₂, у₃, у₄), т. е. N = 4, и две экзогенные (х_1, х₂).

Первое уравнение: Н = 3 (у_1, у₃, у₄ присутствуют), D= 2 (х₁, х₂ отсутствуют) и D = H - 1, поэтому уравнение точно идентифици­руемо (необходимое условие).

Для проверки на достаточное условие идентификации выпишем матрицу А коэффициентов при переменных, не входящих в первое уравнение:

Уравнение	у2	х1	х2
2	-1	а21	0
3	0	а31	0
4	1	0	1

Определитель матрицы detA= , следовательно, ранг мат­рицы равен 3 N- 1, т. е. достаточное условие идентификации вы­полняется, и первое уравнение точно идентифицируемо.

Второе уравнение: Н = 2 (у₂, у₃ присутствуют), D = 1 (х₂ отсут­ствует) и D= Н - 1, поэтому уравнение точно идентифицируемо (необходимое условие).

Выпишем матрицу А коэффициентов при переменных, не вхо­дящих во второе уравнение:

Уравнение	у1	у4	х2
1	-1	β14	0
3	0	β34	0
4	1	-1	1

Выполняется также достаточное условие идентификации: detА = -β₃₄ , ранг матрицы равен 3 N- 1.

Третье уравнение: Н = 2 (у₃, у₄ присутствуют), D = 1 (х₂ отсут­ствует) и D = Н - 1, поэтому уравнение точно идентифицируемо (необходимое условие).

Выпишем матрицу А коэффициентов при переменных, не вхо­дящих в третье уравнение:

Уравнение	у1	у2	х2
1	-1	0	0
2	0	-1	0
4	1	1	1

Здесь также выполняется достаточное условие идентификации: detА = 1, ранг матрицы равен 3 N - 1.

Четвертое уравнение представляет собой тождество, парамет­ры которого известны, поэтому необходимости в его идентифика­ции нет.

Таким образом, все уравнения модели точно идентифициро­ваны. ▲

Пример 8.11. Выполним идентификацию следующей модели:

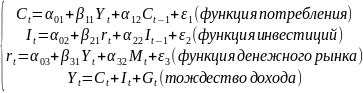
где С— расходы на потребление;

У— совокупный доход;

I— инвестиции;

r— процентная ставка;

М— денежная масса;

G— государственные расходы;

t— текущий период;

t-1 — предыдущий период.

В данной модели четыре эндогенные переменные ( ), N = 4, и четыре экзогенных (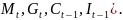

Для первого уравнения: Н = 2 (С_t, У, присутствуют), D = 3 (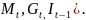 отсутствуют) и D > H- 1, поэтому уравнение сверхидентифи­цируемо (необходимое условие).

Для проверки на достаточное условие идентификации выпишем матрицу коэффициентов при переменных, не входящих в первое уравнение

Минор 3-го порядка данной матрицы следовательно, ранг матрицы равен 3 N – 1, т.е достаточное условие идентификации выполняется.

Для второго уравнения: H = 2 ( присутствуют), D = 3 ( отсутствуют) и D> H- 1, поэтому уравнение сверхиденти­фицируемо.

Выпишем матрицу коэффициентов при переменных, не входя­щих во второе уравнение:

Минор 3-го порядка данной матрицы следовательно, ранг матрицы равен 3 N – 1, т.е достаточное условие идентификации выполняется.

Для третьего уравнения: Н = 2 (У_t, r_t, присутствуют), D= 3 (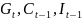 отсутствуют) и D > H - 1, поэтому уравнение сверхиденти- фицируемо.

Выпишем матрицу коэффициентов при переменных, не входя­щих в третье уравнение:

Минор 3-го порядка данной матрицы следовательно, ранг матрицы равен 3 N – 1, т.е достаточное условие идентификации выполняется.

Четвертое уравнение представляет собой тождество, парамет­ры которого известны и необходимости в его идентификации нет. Таким образом, все уравнения модели сверхидентифицированы. ▲

Выводы

Для установления идентифицируемости можно использовать ИП или условия для идентификации.

Для решения точно идентифицируемого уравнения применяется КМНК, а для решения сверхидентифицированного уравнения — ДМНК.

Для точно идентифицированной системы применение к ней КМНК или ДМНК дает одинаковые результаты.

Сверхидентифицируемая структурная модель может быть двух типов:

• все уравнения системы сверхидентифицируемы;

• система наряду со сверхидентифицируемыми содержит точно идентифицируемые уравнения.

Если все уравнения системы сверидентифицируемы, то для оценки структурных коэффициентов каждого уравнения использу­ется ДМНК.

Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приве­денных уравнений.

Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.

ЛИТЕРАТУРА

1. Эконометрика / Под ред. И. И. Елисеевой. — М.: Проспект,

2009.

2. Эконометрика / Под ред. В. С. Мхитаряна. — М.: Проспект, 2009.

3. Плохотников К. Э. Основы эконометрики в пакете SТАТISТIСА: Учеб. пособие. — М.: Вузовский учебник, 2010.

4. Замков О. О. Эконометрические методы в макроэкономиче­ском анализе: Курс лекций. — М.: ГУ ВШЭ, 2001.

5. Просветов Г. И. Эконометрика: Учебно-методическое посо­бие. — М.: РДЛ, 2005.

6. Доугерти К. Введение в эконометрику: Пер. с англ. — М.: ИНФРА-М, 1999.

7. Магнус Я. Р., Катышев П. К, Пересецкий А. А. Эконометри­ка: Начальный курс. — М.: Дело, 2005.