
- •Содержание
- •Приложения…………………………………………………………. 72
- •Изучение электронного осциллографа
- •Устройство и принцип действия осциллографа
- •Порядок выполнения работы
- •Исследование электростатических полей
- •Сведения из теории
- •Моделирование электрического поля и описание установки
- •Порядок выполнения работы
- •Определение эдс источника тока компенсационным методом
- •Сведения из теории
- •Принцип работы потенциометра
- •Порядок выполнения работы
- •Градуировка термопары
- •Сведения из теории
- •Порядок выполнения работы
- •Определение магнитной индукции в межполюсном зазоре прибора магнитоэлектрической системы
- •Сведения из теории
- •Принцип действия прибора магнитоэлектрической системы
- •Порядок выполнения работы
- •Исследование магнитного поля кругового тока
- •Сведения из теории
- •Порядок выполнения работы
- •Описание установки и теория метода определения магнитного поля Земли
- •Порядок выполнения работы
- •Изучение явлений электромагнитной индукции и взаимоиндукции
- •Сведения из теории
- •Описание установки и метода исследования
- •Порядок выполнения работы
- •Исследование кривых гистерезиса ферромагнетиков с помощью осциллографа
- •Сведения из теории
- •Описание метода и экспериментальной установки
- •Порядок выполнения работы
- •Изучение затухающих электромагнитных колебаний в контуре
- •Сведения из теории
- •Описание установки
- •Порядок выполнения работы
- •Исследование зависимости сопротивления проводника от температуры
- •Сведения из теории
- •Описание установки и метода измерений
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Литература
- •Пример обработки результатов прямого измерения
- •Пример обработки результатов косвенного измерения
Сведения из теории
Движущиеся заряды (токи) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Наличие магнитного поля проявляется в действии силы на движущиеся в нем заряды (токи).
Если в магнитное
поле поместить небольшую свободно
ориенти-рующуюся (поворачивающуюся до
тех пор, пока действует вращающий
момент) рамку с током, то она установится
определенным образом. Следовательно,
магнитное поле имеет направленный
характер и должно характеризоваться
векторной величиной. Эту величину
называют индукцией магнитного поля
(магнитной индукцией) и обозначают
![]() .
.
За направление вектора принимают направление положительной нормали (положительная нормаль к плоскости рамки образует правый винт с направлением тока в рамке), установившейся и свободно ориентирующейся небольшой рамки с током.
Согласно гипотезе Ампера в постоянных магнитах в частности, в магнитной стрелке, круговые «молекулярные токи» расположены в параллельных плоскостях и направлены в одну сторону. Благодаря этому действие магнитного поля на магнитную стрелку аналогично действию на рамку с током. Поэтому за направление вектора берут также направление, в котором устанавливается северный конец магнитной стрелки, помещенный в данную точку поля.
Сила
![]() ,
действующая на элемент проводника
длиной
,
действующая на элемент проводника
длиной
![]() с током I,
находящийся в магнитном поле, определяется
по закону Ампера
с током I,
находящийся в магнитном поле, определяется
по закону Ампера
![]() ,
(5.1)
,
(5.1)
или в скалярной форме
dF = B I dl sin
(
![]() ),
(5.2)
),
(5.2)
здесь
![]() -
вектор с модулем dl,
направленный по току, а
и есть индукция магнитного поля в месте,
где расположен элемент проводника.
-
вектор с модулем dl,
направленный по току, а
и есть индукция магнитного поля в месте,
где расположен элемент проводника.
Из формулы (5.2) при
sin![]() =1
=1
![]() (5.3)
(5.3)
Следовательно, вектор магнитной индукции численно равен отношению силы, действующей со стороны магнитного поля на элемент проводника с током, к произведению силы тока на длину элемента, если он расположен перпендикулярно вектору магнитной индукции.
Если индукция в каждой точке поля одинакова, то такое поле называется однородным. В случае однородного магнитного поля и прямого проводника с током, расположенного перпендикулярно линиям индукции, из формулы (5.2) получим
F = B I l . (5.4)
Из формулы (5.4) имеем
![]() ,
,
что позволяет простейшим образом установить единицу измерения магнитной индукции B. В СИ магнитная индукция измеряется в теслах (Тл). Тесла есть индукция такого однородного магнитного поля, в котором на проводник с током в 1 ампер длиной 1 метр, расположенный перпендикулярно линиям индукции, действует сила в 1 ньютон.
Примером практического применения действия магнитного поля на проводник с током служат электроизмерительные приборы магнито-электрической системы.
Принцип действия прибора магнитоэлектрической системы

Для уменьшения трения ось рамки оканчивается стальными кернами, опирающимися на подпятники, изготовленные из агата, рубина или корунда. С осью жестко связана стрелка прибора.
При включении прибора в электрическую цепь ток проходит по виткам рамки. При этом на каждую сторону рамки, расположенную в магнитном поле зазора, действует сила . С учетом числа витков рамки k согласно закону Ампера (5.4) имеем

F = k B I l1 , (5.5)
здесь B - величина магнитной индукции в зазоре; I - сила тока в рамке; l1 - длина той стороны рамки, которая расположена в зазоре; направление силы F определяется правилом ”левой руки” (линии магнитной индукции входят в ладонь, четыре пальца направлены по току, отогнутый большой палец показывает направление силы). Каждая из сил создает вращающий момент рамки, модуль которого равен
M1 = k B I l1 l2 / 2,
где l2 - длина стороны рамки, не помещенной в зазор.
Направление
вектора
![]() 1
можно определить по правилу ”правого
винта”: если вращать винт так, как
вращает рамку приложенная сила, то
поступательное движение винта указывает
направление вектора
1
можно определить по правилу ”правого
винта”: если вращать винт так, как
вращает рамку приложенная сила, то
поступательное движение винта указывает
направление вектора
![]() .
На рис.5.2 вектор
направлен по оси вращения рамки к нам
и обозначен точкой.
.
На рис.5.2 вектор
направлен по оси вращения рамки к нам
и обозначен точкой.
Момент пары сил, приложенных к рамке
M = 2 M1 = k B I l1 l2 = k B I S , (5.6)
где S - площадь рамки.
Величину k I S обозначают рm и называют магнитным моментом рамки. Эту величину вводят как вектор и направляют по положительной нормали к рамке с током. Следовательно,
![]() ,
,
где
![]() - единичный вектор вдоль положительной
нормали к рамке.
- единичный вектор вдоль положительной
нормали к рамке.
С введением вектора Pm выражение (5.5) можно записать в векторной форме:
![]() ,
(5.7)
,
(5.7)
здесь - магнитная индукция в тех местах зазора, где расположена рамка.
Используя закон Ампера, нетрудно показать, что формула (5.7) справедлива также в случае, когда рамка с током расположена в однородном магнитном поле с индукцией .
При изменении направления тока в рамке направление каждой из сил изменится на противоположное и, следовательно, стрелка будет отклоняться в другую сторону от положения равновесия. Поэтому магнитоэлектрический измерительный механизм пригоден только в цепях постоянного тока.
Для компенсации момента служат пружины, скрепленные одним концом с осью рамки. При повороте рамки пружины создают момент сил упругости, пропорциональный углу поворота рамки
N = C , (5.8)
здесь C
- жесткость
пружины. Момент
![]() всегда направлен противоположно
вращающему моменту
.
всегда направлен противоположно
вращающему моменту
.
Пока угол поворота мал (| | > | |), рамка продолжает вращаться под действием результирующего момента M - N. При этом угол увеличивается и вместе с ним увеличивается и N. Это происходит до тех пор, пока момент сил упругости пружин N не станет равным вращающему моменту M. Следовательно, угол, соответствующий установившемуся положению равновесия рамки, будет удовлетворять, согласно (5.6) и (5.8), равенству
C = k B I S . (5.9)
Из формулы (5.9) следует, что угол поворота рамки пропорционален току в ней. Поэтому шкала прибора магнитоэлектрической системы равномерная.
По формуле (5.9) индукция магнитного поля в зазоре
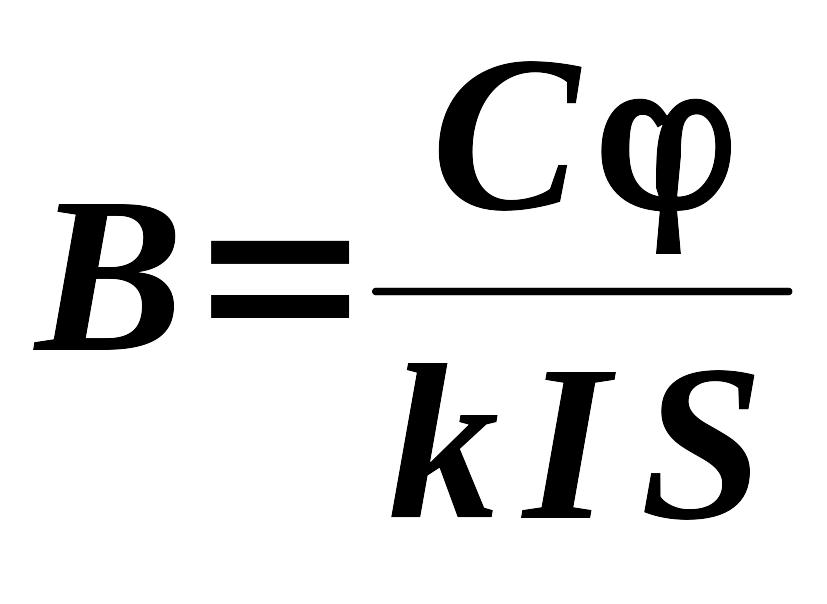 ,
(5.10)
,
(5.10)
что позволяет определить ее опытным путем, если измерить каким-либо образом величины C, , k, S .
