
Задача №1

Коло (рис.1) має параметри R1=2 Oм; R2=1 Ом; R3=5 Ом; E1=8 В; E2=30 В.
Розрахувати струми у всіх вітках методом контурних струмів, прийнявши за незалежні контури R1-R2-E2-E1 і R2-R3-E2.
Рис.1
Розв'язок
1. Оберемо
напрямок контурних струмів
![]() за годинниковою стрілкою.
за годинниковою стрілкою.
2. Система контурних рівнянь:
![]()
3. Після підстановки заданих значень параметрів елементів система матиме вигляд:
![]()
![]()
4. Розв′яжемо систему рівнянь:
![]()
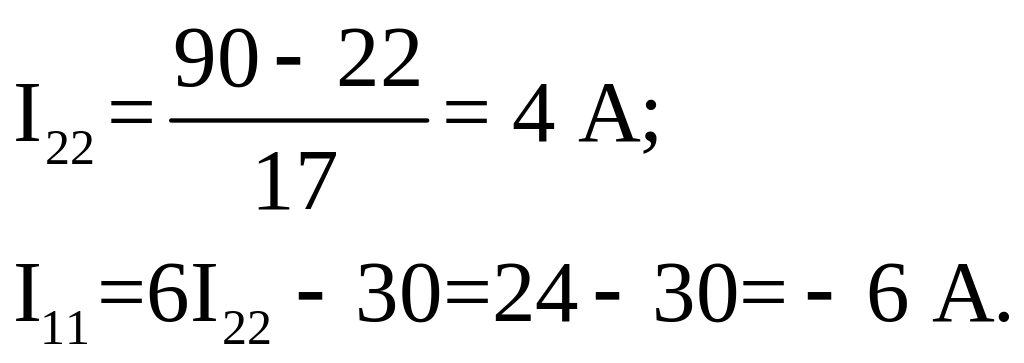
5. Тоді за першим законом Кірхгофа струми у вітках:
![]()
Відповідь:
![]()
Задача №3
З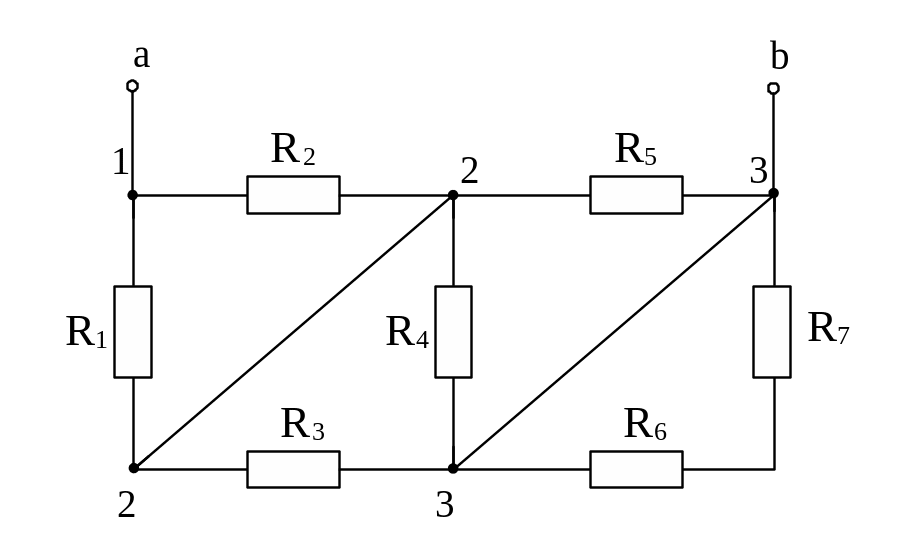 найти
еквівалентний опір кола (рис.1) між
затискачами а і б, якщо Rі=10
Ом,
і=
найти
еквівалентний опір кола (рис.1) між
затискачами а і б, якщо Rі=10
Ом,
і=![]() .
.
Рис.1
Розв’язок
1. Перетворимо схему кола з урахуванням того, що резистори R6 і R7 – закорочені, а R1, R2 та R3, R4, R5 – з’єднані паралельно (рис.2):
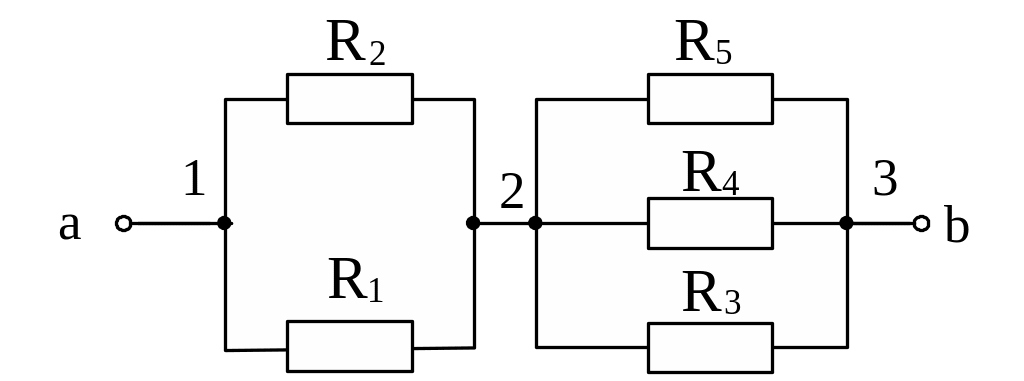
Рис.2
2. Знайдемо еквівалентні опори паралельно з’єднаних резисторів:
![]()
![]()
![]() Ом.
Ом.
3. Тоді еквівалентний опір вихідного кола дорівнює:
Rекв=![]() +
+![]() =5+3.33=8.33
Ом.
=5+3.33=8.33
Ом.
Відповідь:
Rекв=8.33 Ом.
Задача №4
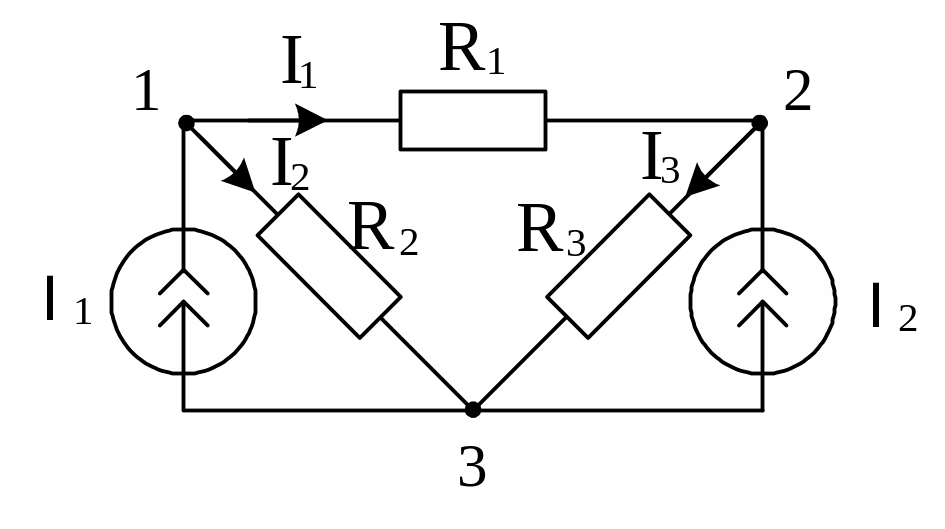
Два джерела струму I1=100 мА і I2=50 мА включені в схему, яка має опори R1=30 Ом; R2=20 Ом; R3=50 Ом. Розрахувати всі струми схеми (рис.1) методом вузлових потенціалів, взявши за базисний третій вузол.
Рис.1
Розв’язок
1. Система рівнянь для контура за методом вузлових потенціалів:
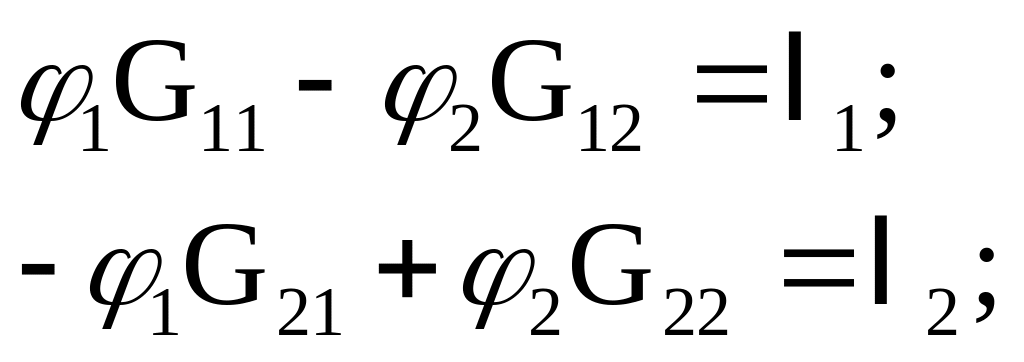
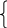
де Gii,
Gij
![]() вузлова та спільна провідності відповідно,
Iі
вузловий
струм, i, j – номери вузлів.
вузлова та спільна провідності відповідно,
Iі
вузловий
струм, i, j – номери вузлів.
2. Вузлова та спільна провідності:
![]() ;
;
![]() ;
;
![]()
3 . Система рівнянь після підстановки отриманих значень набуває вигляду:
![]()
4. Розв’яжемо систему методом Крамера.
Визначник системи:
 См2.
См2.
Детермінанти
![]() та
та
![]() :
:
 См ∙А;
См ∙А;
 См ∙А.
См ∙А.
5. Потенціали вузлів:
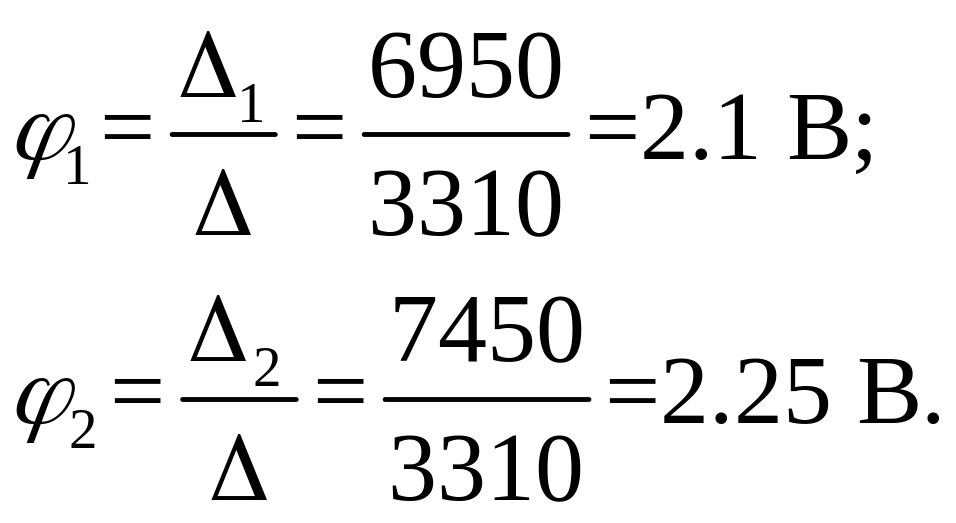
6. Струми в вітках кола:
![]()
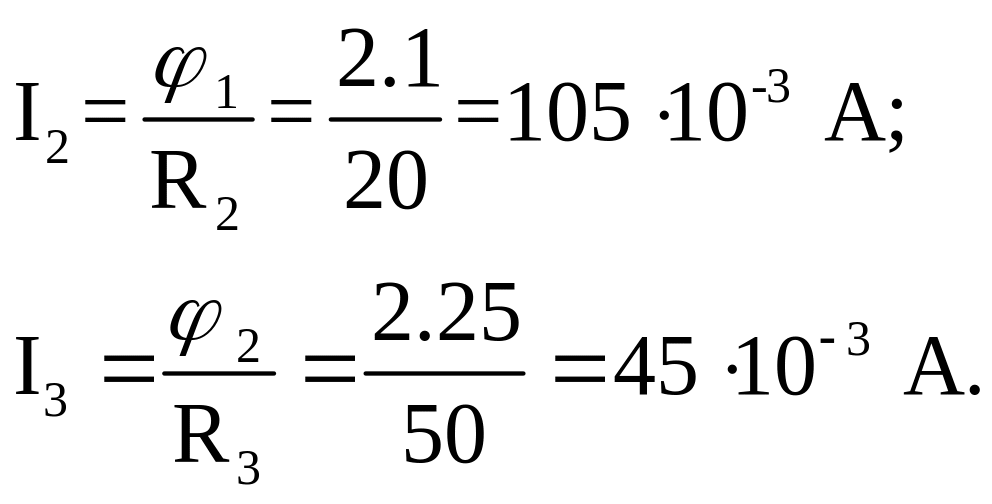
Відповідь:![]()
Задача №5
М етодом
еквівалентного генератора напруги
знайти струм І5, якщо R1=R2=40
Ом; R3=10
Ом; R4=160
Ом;
R5=20
Ом;
E1=E2=20
В
(рис.1).
етодом
еквівалентного генератора напруги
знайти струм І5, якщо R1=R2=40
Ом; R3=10
Ом; R4=160
Ом;
R5=20
Ом;
E1=E2=20
В
(рис.1).
Розв’язок
1. Замінимо частину схеми, за винятком вітки з резистором R5, еквівалентним генератором напруги з ЕРС Еекв та внутрішнім опором Rекв (рис.2):
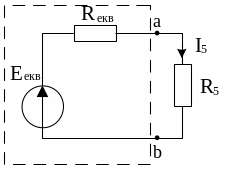 Рис.2
Рис.2
Рис.1
Тоді
струм
![]() .
.
2. Для того, щоб знайти ЕРС Еекв, від’єднаємо вітку ab. Тоді еквівалентний генератор буде працювати в режимі холостого ходу.
Для
розрахунку значення еквівалентної ЕРС
Еекв перетворимо вихідну схему до
вигляду, приведеного на рис.3. Напрямки
струмів
![]() та
та
![]() обираємо
довільно.
обираємо
довільно.
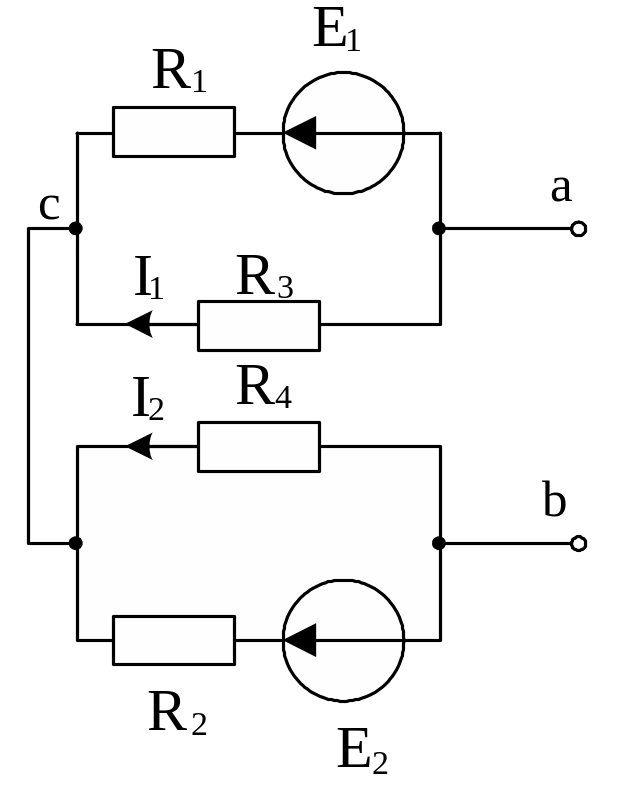
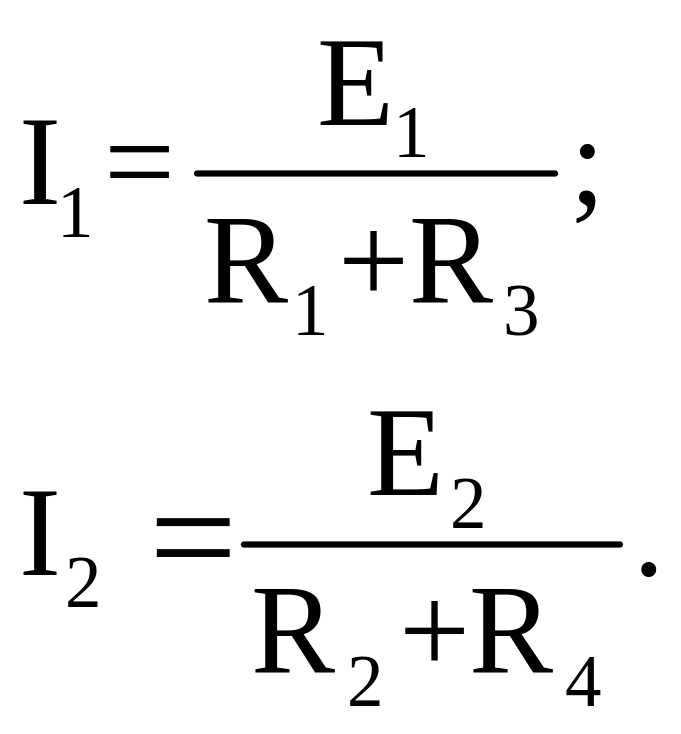
Еекв шукаємо як різницю потенціалів між вузлами a i b:
![]()
Рис.3
3. Знайдемо еквівалентний опір генератора Rекв відносно вузлів а i b; для цього ЕРС усіх джерел в схемі (рис.3) прирівнюємо до нуля:
![]()
4. Шуканий струм І5:
![]()
Відповідь:
![]()
Задача №7
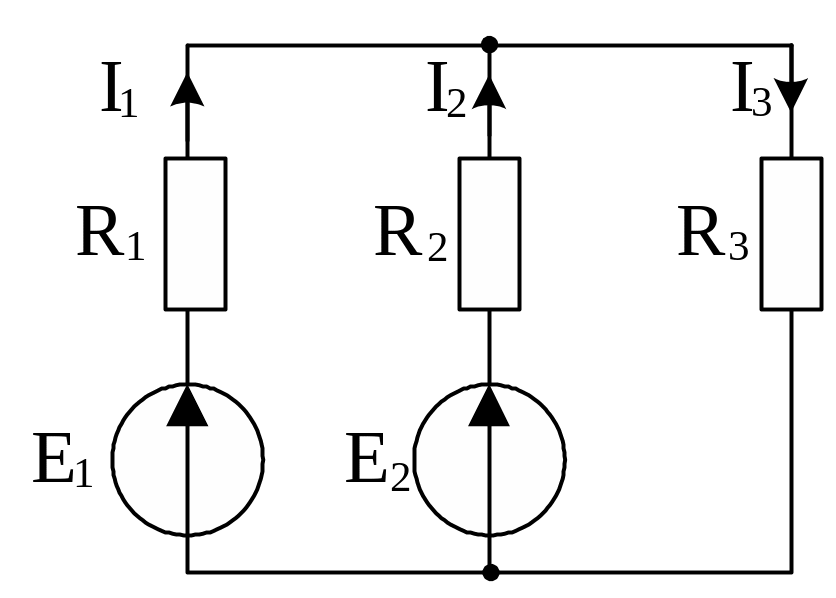
Методом накладання визначити струми в колі(рис.1), якщо
R1=2 Ом; R2=1 Ом; R3=5 Ом; E1=8 В; E2=30 В.
Розв’язок
1. Виключаємо джерело ЕРС Е2, залишаючи від нього тільки його внутрішній опір R2 (рис.2):
Рис.1
2. Розрахуємо часткові струми:
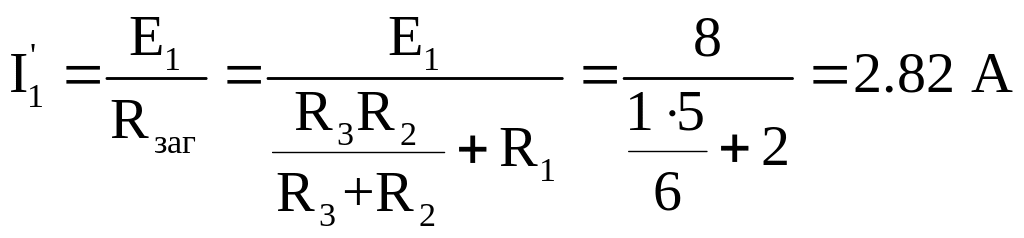 ;
;
![]() ;
;
![]() .
.
3 .
Виключимо
джерело ЕРС Е1, залишивши його внутрішній
опір R1
(рис.3), та знайдемо нові значення часткових
струмів:
.
Виключимо
джерело ЕРС Е1, залишивши його внутрішній
опір R1
(рис.3), та знайдемо нові значення часткових
струмів:
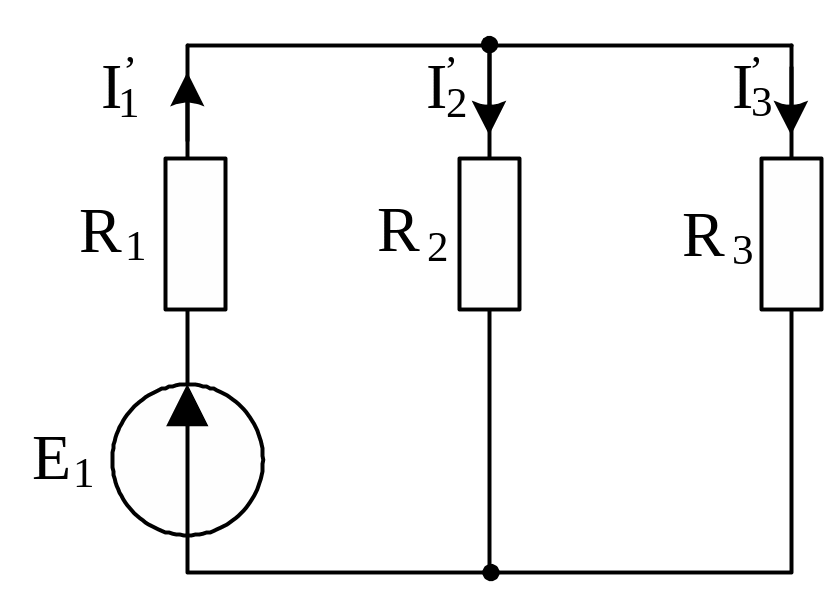
Рис.2 Рис.3
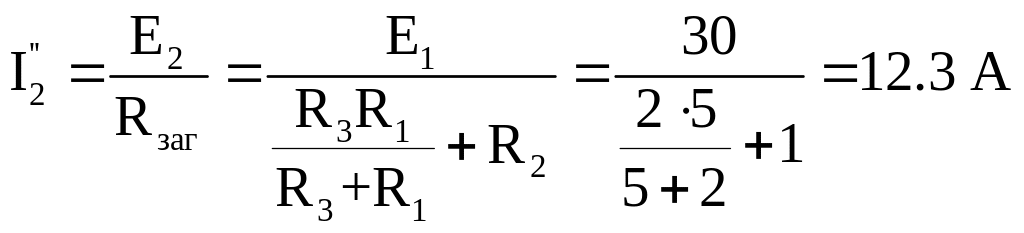 ;
;
![]() ;
;
![]()
4. Знайдемо шукані струми у вітках:
![]()
![]()
![]()
Відповідь:
![]()
Задача №9
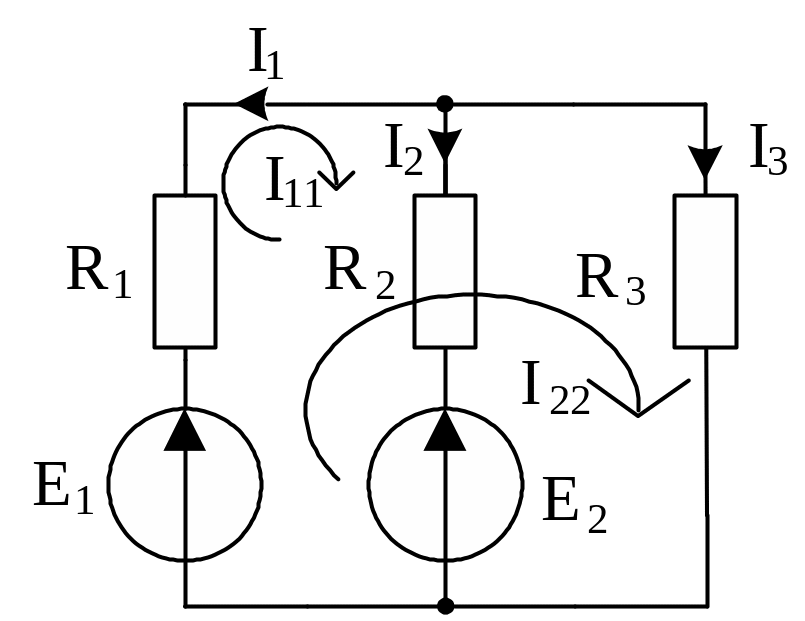
Коло (рис.1) має параметри R1=4 Ом; R2=2 Ом; R3=10 Ом; E1=16 В; E2=60 В. Визначити струми в усіх вітках методом контурних струмів. За незалежні контури узяти R1-R2-E2-E1 і R1- R3- E1.
Рис.1
Розв’язок
1. Оберемо напрямок контурних струмів за годинниковою стрілкою.
2. Складемо систему рівнянь електричної рівноваги кола за другим законом Кірхгофа:
![]()
![]()
3.Підставимо значення параметрів елементів кола та спростимо систему рівнянь:
![]()
![]()
![]()
4.Розвяжемо систему методом Крамера:
Головний визначник системи:
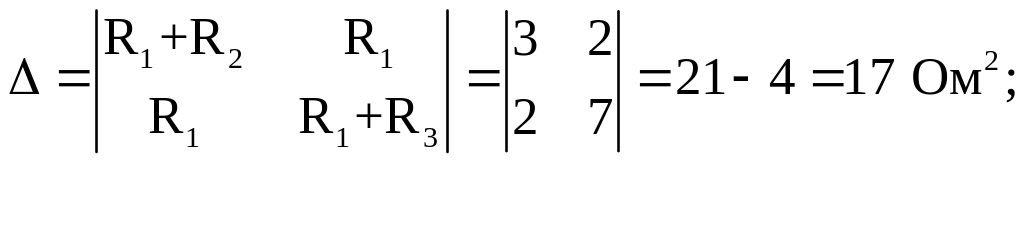
Часткові визначники:
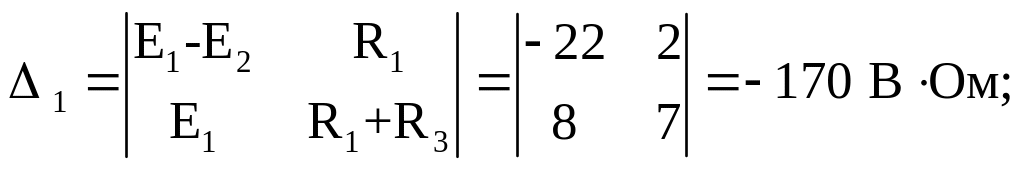
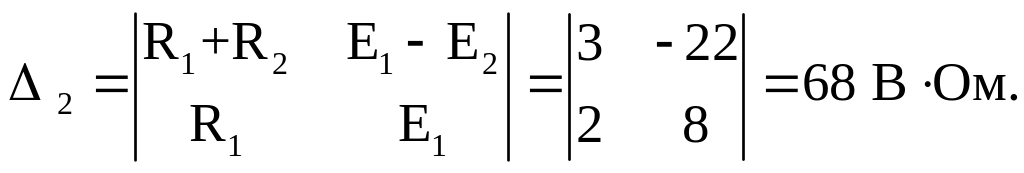
Контурні струми:
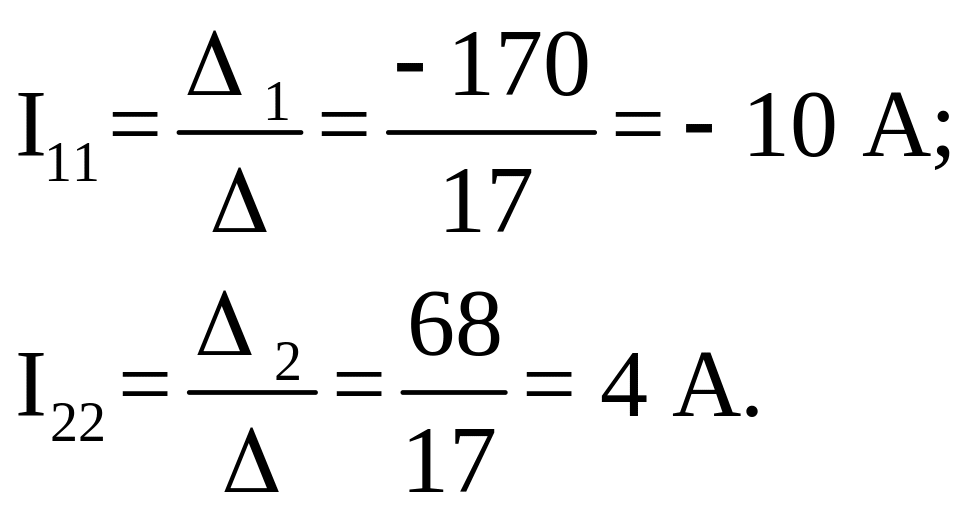
5.Струми в вітках за першим законом Кірхгофа:
![]()
Відповідь:
![]()
