4.2.Гранные поверхности и многогранники

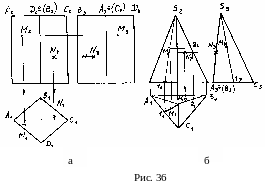
Пирамида - многогранник, одна грань которого (основание) - плоский многоугольник, а другие грани - треугольники с общей вершиной (рис. 36,б).

Призмой называют многогранник, две грани которого равные многоугольники (основания призмы), а все другие (боковые) грани - параллелограммы (рис.36,а). Многоугольник, все грани которого правильные и конгруэнтные многоугольники, называют правильным. Углы при вершинах такого многогранника равны между собой.

Существует пять типов правильных многогранников, которые называют телами Платона - тетраэдр, гексаэдр, октаэдр, додекаэдр, икосаэдр. Призма на чертеже задается проекциями ее оснований и боковых ребер (рис.36,а), пирамиды - проекциями основания, вершины и боковых ребер (рис.36,б). Для изображения призмы или пирамиды целесообразно расположить основания параллельно плоскости проекций.

Точку на гранных поверхностях строят с помощью линий, включающих в себя заданные точки. Целесообразно, чтобы вспомогательные линии, проходящие через заданную точку многогранника, были параллельны одному из ребер или проходили через вершину. Таким образом, построены проекции точек M и N на поверхностях призмы и пирамиды при заданных проекциях M₂ и N₂ (рис.36 а, б).

4.3. Изображение поверхностей вращения

Поверхность, образованная вращением произвольной образующей линии l (прямой или кривой) вокруг неподвижной оси, называют поверхностью вращения. Образующая может быть плоской или пространственной кривой. Каждая точка (А, В, С, D), вращаясь вокруг оси, описывает окружность с центром на оси. (рис. 37). Эти окружности называют параллелями. Наибольшую и наименьшую параллели называют экватором и горлом поверхности. Линии,

по которым плоскости, проходящие через ось, пересекают поверхность, называют меридианами. Рассмотрим некоторые виды поверхностей вращения, образующей которых является прямая линия.

Цилиндр вращения получается вращением прямой l вокруг оси j , при этом l||j (рис. 38). Определитель поверхности - образующая l и ось j.

Проекции точек на цилиндре, заданных одной проекцией (например Е₂, F_3; рис.39), необходимо строить с помощью образующих линий, которым принадлежат проекции точек с учетом их видимости.

Конус вращения - это поверхность, которую получают вращением прямой образующей l вокруг оси и пересекающейся с ней (l∩j); ( рис.39).

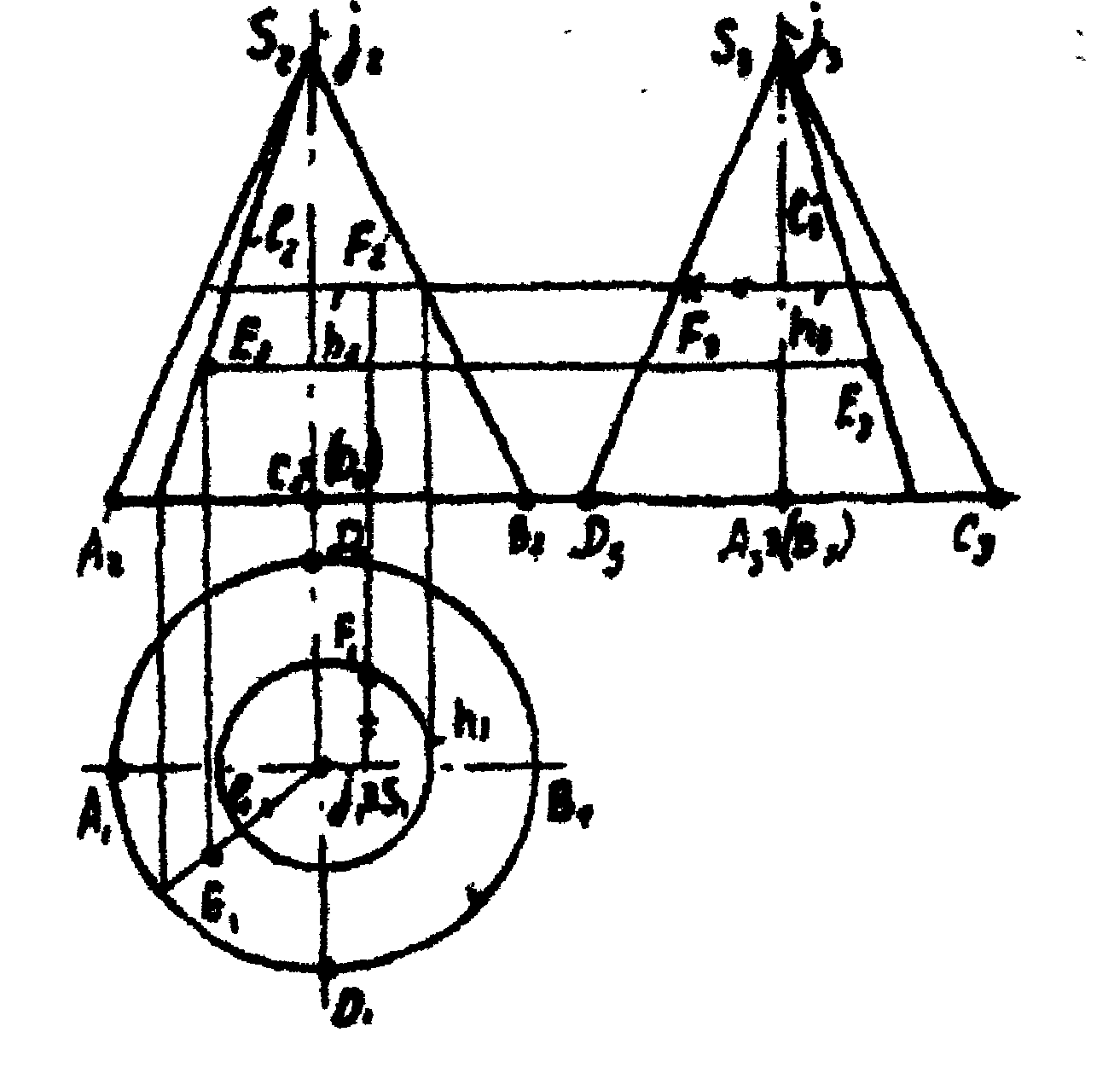
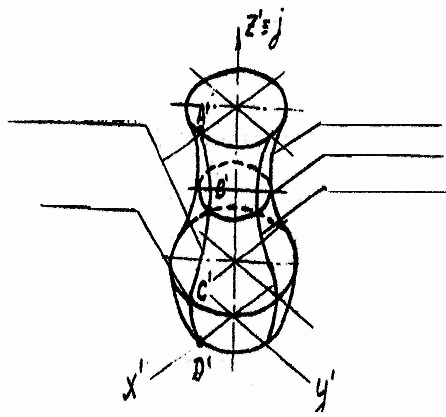
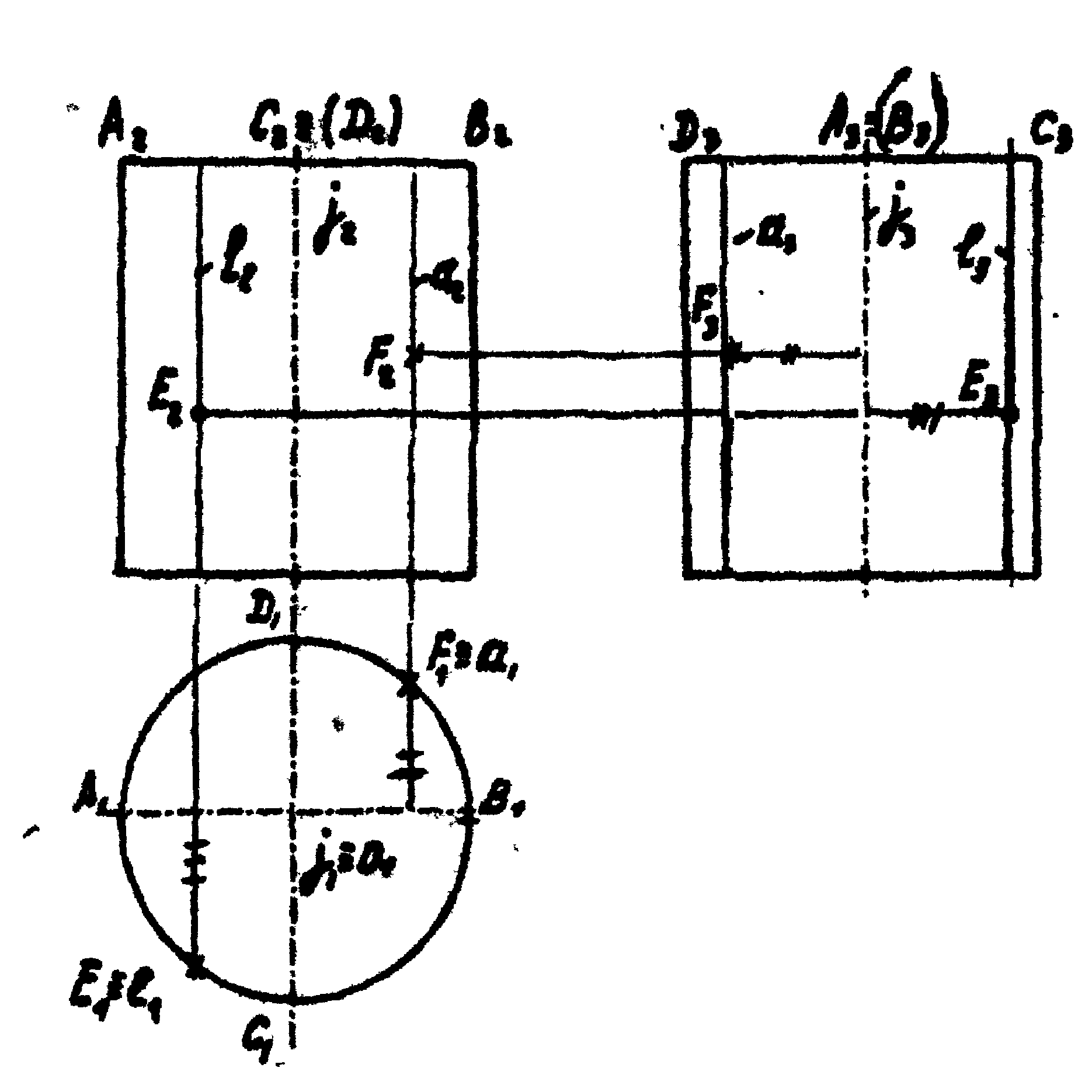
Рис. 38

Рис. 39

Гранные поверхности образуют перемещением прямолинейной образующей l по ломанной направляющей m . При этом, если одна точка S образующей неподвижна, получится пирамидальная поверхность (рис.40,а), если образующая l параллельна заданному направлению (q,) то получится призма

тическая поверхность (рис.40,б). Определителем пирамидальной поверхности является: S  l, l∩m, призматической (l||р; l∩m).

Рис. 40

А₂

j₂

g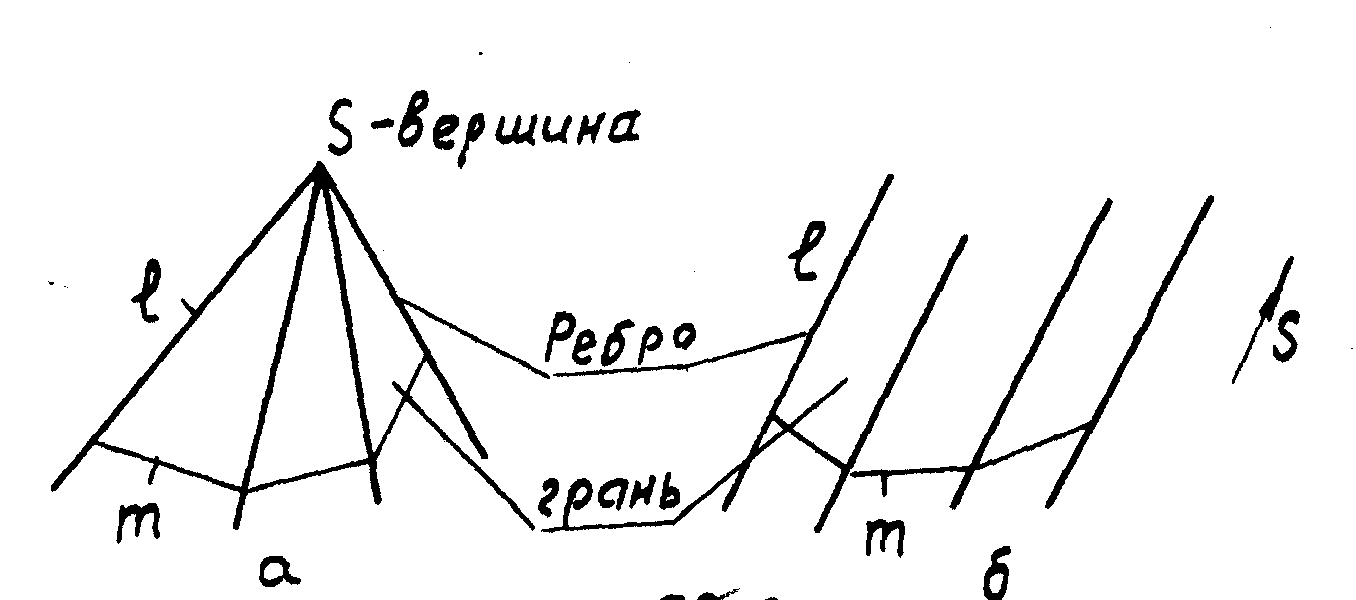

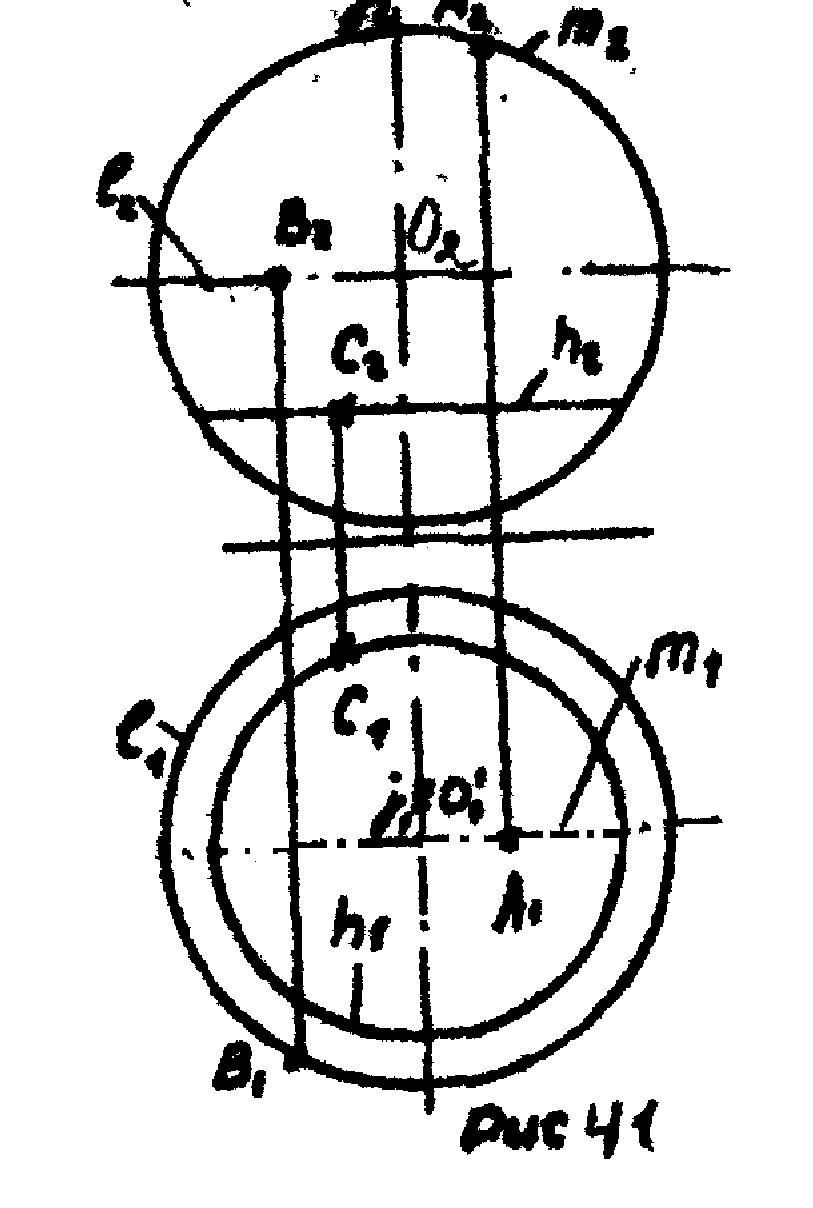
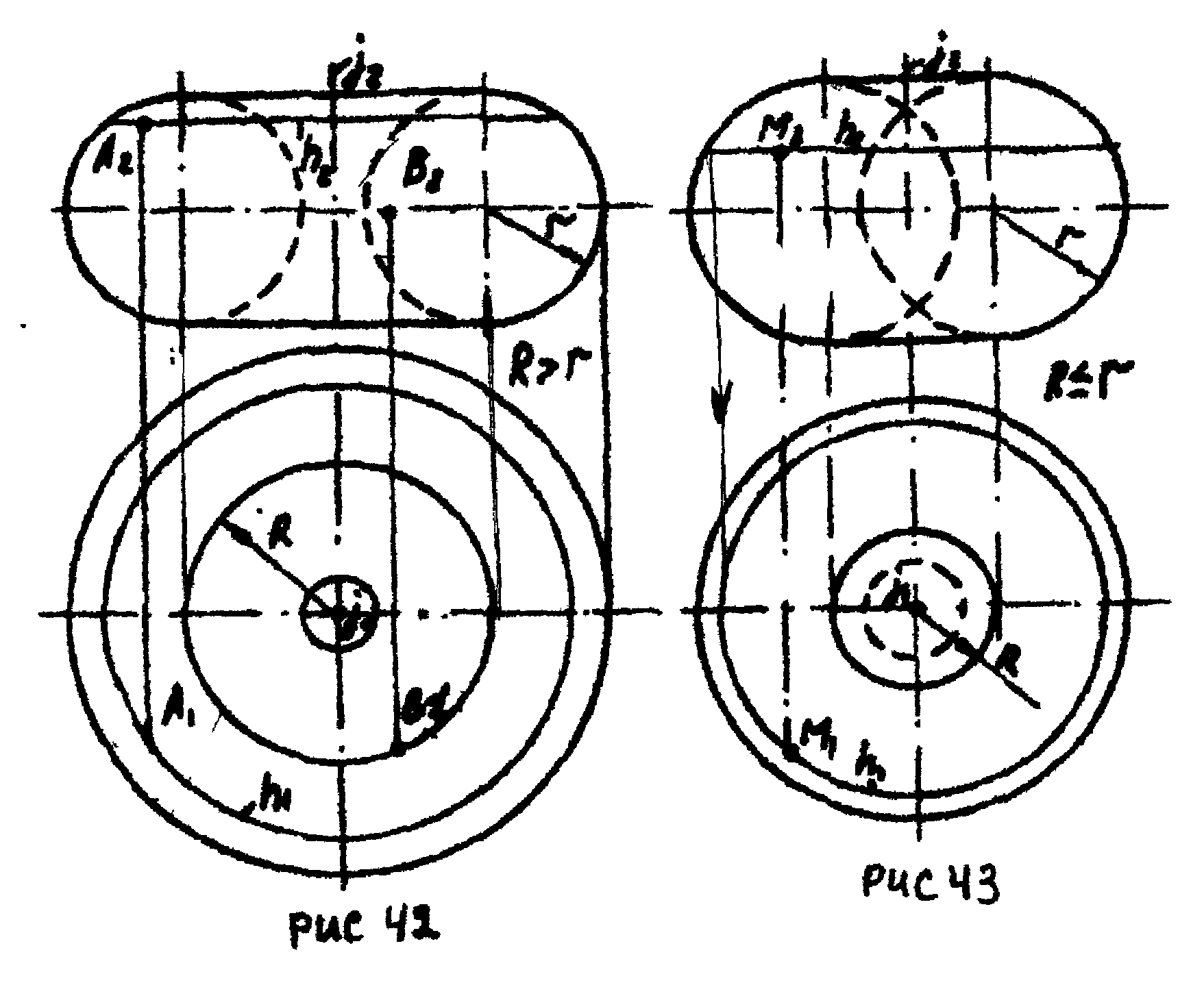
Рис. 41

Рис. 43

Р

Рис. 42

ассмотрим поверхности, получаемые вращением образующей в виде окружности вокруг оси j.

Сфера получается вращением окружности вокруг её диаметра, а центр образующей окружности лежит на оси вращения (Oj) Точка А на поверхности сферы принадлежит главному меридиану m(A₂A₁). Точка В - экваторуl (B₂B₁), точка С (задана проекция С₂) построена с помощью вспомогательной параллели h(h₂,h₁) рис.41.

Тор - поверхность, образованная вращением окружности вокруг оси j, которая лежит в плоскости окружности и не проходит через её центр. Поверхности тора делят на:

-открытый тор - ось j проходит вне окружности (рис. 42).

-закрытый тор - ось j пересекает окружность, или касается её (рис. 43).

Проекции точек на этих поверхностях строят, пользуясь горизонтальными, фронтальными и профильными параллелями. На рис. 42,43 показаны построения проекции А_1, В_2, М₁ по заданным А₂, В₁, М_2.