3.3. Напівлогарифмічні моделі

Моделі виду Ln Y = βо + βХ + u, (11) , Y = βо + β lnХ + u (12)

називаються напівлогарифмічними моделями.

Лог - лінійна модель

Напівлогарифмічна модель (11) легко зводиться до лінійної моделі заміною Y* = 1пY. Коефіцієнт β y моделі (11) характеризує темп приросту змінної Y по змінній X, тобто характеризує відношення відносної зміни Y до абсолютної зміни X. Дійсно, продиференціювавши (11) по X, маємо:

,

Помноживши β на 100, одержимо процентну зміну змінної Y (темп приросту змінної Y). Тому напівлогарифмічна модель (11) зазвичай використовується для вимірювання темпу приросту економічних показників: наприклад, при аналізі банківського вкладу за первісним внеском й процентною ставкою, при дослідженні залежності приросту об'єму випуску від відносного (процентного) збільшення витрат ресурсу, бюджетного дефіциту від темпу росту ВНП, темпу росту інфляції від об'єму грошової маси тощо.

До такої моделі зводиться залежність, відомa в банківському й фінансовому аналізі:

Y_t = Y₀ (1 + r ) ^t, (13)

де Y_о - початкова величина змінної Y (наприклад, первісний внесок у банку);

r - складний темп приросту величини Y (процентна ставка);

Y_t - значення величини Y нa момент часу t (внесок дo банкy нa момент часу t).

Прологарифмувавши (13), маємо: 1п Y_t = 1п Y₀ + t ·1п(1 + r).

Уведемо позначення: 1п Y₀ = β₀ , 1п(1 + r) = β. Тоді (13) прийме вид:

1п Y_t = β₀ + β t + u _t. (14)

В (14) використали додатково випадковий доданок u_t ( вразі можливої мінливості процентної ставки). Крім того, співвідношення β = 1п(1 + r) визначає темп приросту r показника Y:

1 + r = e^β, r = 1 - e^β.

При цьому коефіцієнт β визначає миттєвий темп приросту, а коефіцієнт r – узагальнений (складний) темп приросту величини Y.

Лінійно – логарифмічна модель

Лінійно-логарифмічна модель – це модель виду Y = βо + β ln Х + u, (12)

яка зводиться до лінійної моделі заміною Х* = 1пХ.

Коефіцієнт β y моделі (11) характеризує зміну фактора Y внаслідок одиничного відносного приросту змінної X ( на 1%), тобто характеризує відношення абсолютної зміни Y до відносної зміни X. Дійсно, продиференціювавши (11) по X, маємо:

,

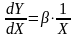Помноживши останнє співвідношення на 100, одержимо абсолютний приріст змінної Y за процентної зміни фактора Х. Тому дана модель (11) зазвичай використовується для дослідження впливу процентної зміни незалежного фактора на абсолютний приріст залежної змінної Y.

Якщо Y = GNP ( валовий національний продукт), Х = М ( грошова маса),

то GNP = α + β · ln М + u,

тобто за збільшення пропозиції М ( грошової маси) на 1% ВНП зросте в середньому на 0,01 β.