Лекция 8 Модели состояний и переходов - это частный случай спецификации поведения программ конечными функциями.
Область задания конечной функции (КФ) - конечное множество значений (а область существования – необязательно конечное множество). Простая и наглядная форма задания КФ – таблица с числом входов, равным мощности области задания. Вопрос 1. Так часто представляются эмпирические зависимости, например: K = F ( V ):
-
Скорость V м/с
0,05
0,10
0,20
0,50
Коэффициент трения К
0,21
0,24
0,27
0,31
Частный случай КФ – логическая функция; ей соответствует таблица истинности. Например, логическая функция двух переменных:
-
Концевой выключатель
F
F
T
T
Термореле
F
T
F
T
Сигнал аварии
F
T
F
T
T (True) означает срабатывание датчика, F (False) – его противоположное (исходное) состояние. Таблица истинности – непроцедурная форма описания алгоритма; ее процедурный эквивалент состоит из последовательности блоков выбора (ветвлений).
Очевидно, что непроцедурная форма нагляднее.
Обобщение – многозначная логика: мощность области значений больше двух. Соответ-ствующая таблица называется таблицей решений (ТР). Аргументы называются условиями, значения функции – решениями. Пример: спецификация программы контроля параметров
насоса с электроприводом:
Условия |
Входное напряжение U < 120 в |
N |
N |
N |
N |
N |
Y |
Скорость вращения N < 50 об/с |
N |
N |
Y |
N |
N |
~ |
|
Температура T > 45 C |
Y |
N |
~ |
Y |
N |
~ |
|
Давление P < 1,2 атм. |
Y |
N |
~ |
N |
Y |
~ |
|
Решение |
A |
О |
A |
О |
W |
A |
|
Здесь Y (Yes) заменяет T, N (No) - F, ~ представляет Y или N - для сокращения числа столбцов. Решение A означает аварию, O - нормальное состояние, W - предупреждение.
Подразумевается, что измерения параметров (условий) периодически обновляются, скажем, раз в сек, и решения вычисляются синхронно с циклом опроса датчиков.
Существуют текстовые нотации для ТР - языки ТР - и трансляторы с них на инструмен-тальные языки программирования. Вопрос 2. ТР удобны для проектирования программ промышленной автоматики, решающих задачи логического управления (напр., светофором), диагностики неисправностей и т. д. Достоинства ТР:
Наглядность, непроцедурность - понятность непрофессионалам
ТР одновременно служит планом тестирования. Вопрос 3.
Следующее обобщение - недвоичная область задания. Ему соответствует известная дискретная кибернетическая модель - автомат Мура:
A
x1 y1 Где:
x2 y2 X={x1, ... xn} - вектор входов,
... ... Y={y1,... ym}- вектор выходов
xn ym
Входы и выходы интерпретируются как сигналы; на каждом такте работы автомата возбуждается только один вход и генерируется один выход. Эта модель традиционно используется для описания комбинационных логических схем, т.е. схем без памяти. Соответствие для предыдущего примера: Y={A, O, W}, X={x1,..., x16} - 16 возможных комбинаций четырех двоичных значений (условий в языке ТР).
Дальнейшим обобщением является модель с памятью - автомат Мили, или конечный автомат (КА, FSM - Finite State Machine). Преобразование входа в выход зависит от текущего состояния автомата (из конечного множества), т.е. от предыстории; состояние - тоже функция входов. Более интересна асинхронная модель КА, где входы возбуждаются в непредсказуемые моменты времени: входы - это сигналы, а не условия, как в ТР.
A
X
- множество входов
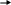S Y - множество выходов (в т. ч. пустой)
T
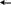si
S - начальное состояние
fy : X S Y - функция выходов
fs : X S S - функция переходов
Т символизирует задержку: от нового состояния будет зависеть реакция на следующий вход. Являясь конечными функциями двух переменных, fy и fs могут быть заданы двумя таблицами или сводной таблицей вида:
|
s1 |
s2 |
... |
sk |
x1 |
s11/ y11 |
s21/ y21 |
... |
sk1/ yk1 |
x2 |
s12/ y12 |
s22/ y22 |
... |
sk2/ yk2 |
... |
... |
... |
... |
... |
xn |
s1n/ y1n |
s2n/ y2n |
... |
skn/ ykn |
Более наглядное их изображение - диаграммой состояний и переходов (STD - State-Transition Diagram) - графом, где вершины - состояния - изображаются кружками, а переходы дугами, нагруженными соответствующими входами и выходами. Ячейке таблицы в i строке и j столбце соответствует фрагмент графа:
si
sij
Наглядность графа выше; степени вершин обычно гораздо меньше n, т.к. многие входы могут не изменять состояния и не вырабатывать никакого выхода.
Пример: модель поведения системы управления роботом. Интерфейс пользователя - пульт управления, схематически изображенный на рис. 8-1.
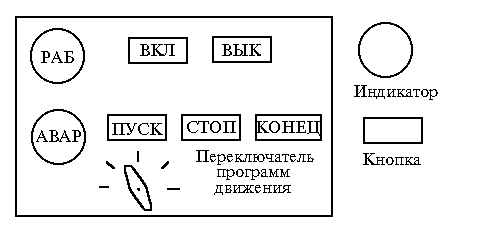
Рис 10-1. Пульт управления роботом
Робот выполняет одну из программ движения, выбранную оператором с помощью переключателя. Спецификация системы управления в нотации языка DARTS (Design Approach Real Time Systems) приведена на рис 8-2. Комментарии к диаграмме:
Входы, написанные наклонным шрифтом, - внутренние (вырабатываются системой), остальные вызваны действиями человека-оператора
Три выхода генерируются автоматом: "Вкл индик РАБ", "Вкл индик АВАР" и "Вык индик РАБ"
Состояние, отмеченное * - любое состояние
Диаграмма успешно заменяет длинное текстовое описание функционирования. Из нее, например, видно, что существуют подготовительный (Запуск) и заключительный (Завершение) этапы работы робота; что переключать программу движения можно только после завершения текущей программы и т.д. В каждом состоянии явно видны возможные действия пользователя. Пути в графе - допустимые маршруты переходов - разрешенные последовательности действий. Вопрос 4.
В то же время алгоритмы работы системы в каждом из состояний не раскрываются - это задача процедурной модели. На самом деле с каждым переходом связан запуск соответствующего программного модуля, именем которого (т.е. выходом) должен быть помечен переход (это опущено в диаграмме, чтобы не загромождать ее). Кроме такой диаграммы, в языке DARTS предусмотрена схема потока данных: датчики программные модули исполнительные устройства. Вместе они служат непроцедурной спецификацией контроллера робота.
Два способа программной реализации КА:
По столбцам таблицы состояний и переходов / выходов: состояние - место в программе, переходы - CASE по входам
По строкам: состояние – значение переменной (флажка), прием входа - место в программе, далее CASE по флажкам для данного входа