3. Ряди в комплексній площині

3.1. Числові ряди

Ряд , (3.1)

членами якого є комплексні числа, називається числовим рядом (у комплексній області). Ряд (3.1) з комплексними членами можна записати у вигляді:

,

де a_n і b_n (n = 1, 2, 3,…)–дійсні числа.

Сума перших n членів ряду (3.1) називається n-ю частинною сумою ряду.

Якщо існує скінчена границя S послідовності частинних сум S_n ряду: 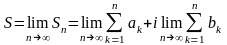, то ряд (3.1) називається збіжним, а S – сумою ряду; якщо 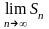не існує, то ряд (3.1) називається розбіжним.

Очевидно, що ряд (3.1) збіжний тоді і тільки тоді, коли збіжний кожний з рядів:

(3.2)

та

(3.3)

При цьому , де S₁ – сума ряду (3.2), а S₂ – сума ряду (3.3). Це означає, що дослідження збіжності ряду з комплексними членами зводиться до дослідження збіжності рядів (3.2) і (3.3) з дійсними членами.

У теорії рядів з комплексними членами основні означення, багато теорем і їх доведення аналогічні відповідним означенням і теоремам з теорії рядів з дійсними членами.

Наведемо деякі з них.

Залишком ряду (3.1) називається різниця

.

Теорема 3.1 (необхідна ознака збіжності ряду). Якщо ряд (3.1) збіжний, то його загальний член при прямує до нуля: .

Ряд (3.1) називається абсолютно збіжним, якщо збіжний ряд

(3.4)

За умовою ряд із загальним членом збіжний. Тоді внаслідок очевидних нерівностей і і згідно ознаки порівняння збіжні ряди і . Звідси випливає збіжність рядів (3.2) і (3.3), а значить, і абсолютна збіжність ряду (3.1).

Якщо ряд абсолютно збіжний і має суму 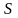, то ряд, отриманий з нього перестановкою членів, також збіжний і має ту ж суму , що і початковий ряд.

Абсолютно збіжні ряди можна почленно додавати та множити.

При дослідженні на збіжність рядів з комплексними членами застосовні усі відомі з дійсного аналізу ознаки збіжності знакопостійних рядів, зокрема ознака Даламбера: якщо існує , то при ряд (3.4) абсолютно збіжний, а при - розбіжний.

3.2. Степеневі ряди

Степеневим рядом у комплексній площині називають ряд виду

, (3.5)

де - комплексні числа (коефіцієнти ряду), - комплексна змінна.

Розглядають також і степеневі ряди вигляду

, (3.6)

які називають рядом за степенями різниці 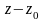, - комплексне число. Підстановкою ряд (3.6) зводиться до ряду (3.5).

Ряд (3.5) при одних значеннях аргументу може збігатися, при інших – розбігатися.

Сукупність усіх значень , при яких ряд (3.5) збіжний, називається областю збіжності цього ряду.

Основною теоремою степеневих рядів є теорема Абеля, що встановлює структуру області збіжності степеневого ряду.

Теорема 3.2 (Абель). Якщо степеневий ряд (3.5) збіжний при (у точці ), то він абсолютно збіжний при всіх значеннях , що задовольняють умові .

Доведення теореми аналогічне доведенню теореми Абеля в дійсному аналізі .

Наслідок 3.1. Якщо ряд (3.5) розбіжний при , то він розбіжний при всіх значеннях , що задовольняють умові (тобто поза кругом радіуса з центром в початку координат).

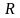Якщо ряд (3.5) має хоча б одну відмінну від нуля точку збіжності, то з теореми Абеля випливає існування числа такого, що при всіх значеннях , що задовольняють нерівності , степеневий ряд (3.5) абсолютно збіжний, а при - розбіжний. Нерівності задовольняють точки комплексної області, що лежать всередині круга радіуса з центром у точці .

Величина називається радіусом збіжності ряду (3.5), а круг - кругом збіжності ряду. У крузі ряд (3.5) збіжний, поза цим кругом – розбіжний; на колі можуть розташовуватися як точки збіжності, так і точки розбіжності ряду.

Прийнято вважати, що , якщо ряд (3.5) збіжний в одній точці ; , якщо ряд збіжний на всій комплексній площині. Кругом збіжності ряду (3.6) є круг з центром у точці .

Радіус збіжності ряду (3.5) можна обчислити за формулою (або ), отриманої після застосування ознаки Даламбера ( Коші) до ряду з модулів членів початкового ряду.

Наведемо (без доведення) деякі властивості степеневого ряду.

1. Сума степеневого ряду усередині круга його збіжності є аналітична функція.

2. Степеневий ряд усередині круга збіжності можна почленно диференціювати і почленно інтегрувати будь-яке число раз. Отриманий при цьому ряд має той же радіус збіжності, що і вихідний ряд.

Приклад 11. Знайти область збіжності ряду .

○ Тут , ,

,

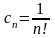тобто . Отже, областю збіжності є вся площина . ●

Приклад 12. Знайти круг збіжності ряду .

○ Тут . Даний ряд збіжний в крузі . ●

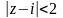Приклад 13. Визначити радіус збіжності ряду та дослідити збіжність ряду в точках , , .

○ Скористаємося ознакою Даламбера. Тут

, , .

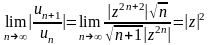Ряд збіжний при всіх , що задовольняють нерівності , тобто . Кругом збіжності є круг з центром у точці і радіусом 1.

Точка лежить усередині круга збіжності, у цій точці ряд збіжний абсолютно. Точка лежить на межі круга збіжності, у цій точці ряд може збігатися (абсолютно або умовно) або розбігатися. Підставляючи значення у вираз загального члену ряду, одержимо . Числовий ряд із загальним членом розбіжний відповідно до інтегральної ознаки Коші . Отже, у точці степеневий ряд розбіжний.

Точка лежить поза кругом збіжності, тому ряд в даній точці розбіжний. ●