2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.

Теорема 2.1 (Коші). Якщо функція f(z) аналітична в однозв'язній області D, то інтеграл від цієї функції по будь-якому замкненому контуру L, що лежить в області D, дорівнює нулю, тобто .

□

Доведемо теорему, припускаючи неперервність похідної f’(z) (це спрощує доведення і не є обмеженням, бо аналітична функція, насправді, має похідні всіх порядків). За формулою (2.2) маємо:

.

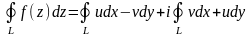Внаслідок аналітичності f(z)=u+iv і неперервності f(z) в однозв'язній області D, функції u=u(x;y) і v=v(x;y) неперервні і диференційовні в цій області і задовольняють умови Ейлера-Даламбера: і . Ці умови означають рівність нулю інтегралів і (Чому?). Отже,

■ Теорема Коші допускає поширення на випадок багатозв’язної області.

Розглянемо для визначеності тризв’язну область D, обмежену зовнішнім контуром L і внутрішніми контурами L₁ і L₂ . Виберемо додатній напрямок обходу контурів: при обході область D залишається ліворуч (див. рис. 8).

Н ехай функція f(z) аналітична в області D і на контурах L, L₁ і L₂ (тобто в замкненій області ; функція називається аналітичною в замкненій області , якщо вона аналітична в деякій області, що містить всередині область D і її межу L).

Провівши два розрізи (дві дуги) і області D (див. Рис. 8), одержимо нову однозв'язну область D₁, обмежену замкненим

Рис. 8 орієнтованим контуром Г, що складається з контурів L, L₁, L₂ і розрізів і : . За теоремою Коші для однозв'язної області

, але , тому що кожний з розрізів (дуг) і при інтегруванні проходиться двічі в протилежних напрямках. Тому одержуємо: , тобто інтеграл від аналітичної в замкнутій області функції f(z) по мажі області D, що обходиться в додатному напрямку, дорівнює нулю.

Зауваження. Змінивши напрямок обходу внутрішніх контурів L₁ і L₂, будемо мати , де всі контури (L, L₁ і L₂) о бходяться в одному напрямку: проти годинникової стрілки (або за годинниковою стрілкою).

Рис. 9 Зокрема, якщо f(z) аналітична в двозв’язній області,

обмеженій контурами L і l і на самих цих контурах (див. рис. 9), то , тобто «інтеграл від функції f(z) по зовнішньому контуру L дорівнює інтегралу від функції f(z) по внутрішньому контуру l» (контури L і l обходять в одному напрямку).

Наслідок 2.1. Якщо f(z) – аналітична функція в однозв'язній області D, то інтеграл від неї не залежить від форми шляху інтегрування, а залежить лише від початкової точки z₀ і кінцевої точки z шляху інтегрування.

Д ійсно, нехай L₁ і L₂ – дві криві в області D, що з'єднують точки z₀ і z (рис. 10).

За теоремою Коші , тобто , або , звідси

Рис. 10 .

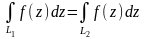У таких випадках, коли інтеграл залежить тільки від початкової точки і кінцевої точки шляху інтегрування, користуються позначенням . Якщо тут зафіксувати точку z₀, а точку z змінювати , то буде функцією від z. Позначимо цю функцію через F(z): . Можна довести, що якщо функція f(z) аналітична в однозв'язній області D, то функція F(z) також аналітична в D, причому

.

Функція F(z) називається первісною для функції f(z) в області D, якщо .

Можна показати, що якщо F(z) є деяка первісна для f(z), то сукупність усіх первісних f(z) визначається формулою F(z)+C, де C=const. Сукупність усіх первісних функцій для f(z) називається невизначеним інтегралом від функції f(z) і позначається символом , тобто , де .

Нехай функція 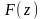є первісна функція для f(z). Отже, . Поклавши тут , одержимо (контур замкнеться, інтеграл дорівнює нулю). Звідси , а отже,

Отримана формула називається формулою Ньютона-Лейбніца.

Інтеграли від елементарних функцій комплексної змінної в області їх аналітичності обчислюється за допомогою тих же формул і методів, що й у дійсному аналізі.

Так, ; ; 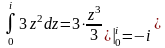і т.д.

Приклад 8. Обчислити інтеграли: а) ; б) , де L є коло радіуса R з центром у точці z₀, обхід протів годинникової стрілки (див. рис. 11).

○ а) Теорема Коші незастосовна, тому що функція не аналітична в точці z₀. Параметричні рівняння кола L : Рис. 11 , , де . Отже, . Таким чином, ми отримали, що комплексно-параметричне рівняння даного кола є , . Тому за формулою (2.4) отримаємо:

.

б) При маємо:

.

Отже,

, , n – ціле, .