
- •Елементи теорії функцій комплексної змінної
- •1. Функції комплексної змінної.
- •1.1. Основні поняття
- •1.2 Границя і неперервність функції комплексної змінної
- •1.3. Основні елементарні функції комплексної змінної
- •1.3.1. Показникова функція
- •1.1.3.2. Логарифмічна функція
- •1.3.5. Тригонометричні функції
- •1.3.6. Гіперболічні функції
- •1.3.7. Обернені тригонометричні і гіперболічні функції
- •1.4. Диференціювання функції комплекснї змінної. Умови Ейлера-Даламбера.
- •1.5. Аналітична функція. Диференціал
- •2. Інтегрування функції комплексної змінної
- •2.1 Означення, властивості і правила обчислення інтеграла
- •2.2. Теорема Коші. Первісна , невизначений інтеграл. Формула Ньютона-Лейбніца.
- •2.3. Інтеграл Коші. Інтегральна формула Коші
- •3. Ряди в комплексній площині
- •3.1. Числові ряди
- •3.2. Степеневі ряди
- •3.3. Ряд Тейлора
- •3.4. Нулі аналітичної функції
- •3.5. Ряд Лорана
- •Ряд Лорана для функції
- •○ Скористаємося відомим розкладом
- •3.6. Класифікація особливих точок.
- •Усувні особливі точки
- •Істотно особлива точка
- •4. Лишок функції
- •4.1. Поняття лишка і основна теорема про лишки
- •4.2. Обчислення лишків. Застосування лишків в обчисленні інтегралів
- •4.3.Теорема Коші про лишки
- •Доведення
1.5. Аналітична функція. Диференціал
Фундаментальним поняттям у теорії функцій комплексної змінної є поняття аналітичної функції.
Однозначна функція f(z) називається аналітичною (голоморфною) у точці z, якщо вона диференційовна (виконані умови Ейлера-Даламбера) у деякому околі цієї точки. Функція f(z) називається аналітичною в області D, якщо вона диференційовна в кожній точці .
Як видно з цього означення, умова аналитичності в точці не збігається з умовою диференційовності функції в цій же точці (перша умова більш сильніша).
Точки площини z, у яких однозначна функція f(z) аналітична, називаються правильними точками f(z). Точки, у яких функція f(z) не є аналітичною, називаються особливими точками цієї функції.
Нехай
функція w=f(z)
аналітична в точці
z.
Тоді
.
Звідси випливає, що
 ,
де
,
де
 при
,
а приріст функції можна записати так:
при
,
а приріст функції можна записати так:
 .
Якщо
.
Якщо
 ,
то перший доданок
,
то перший доданок
 являється при
нескінченно малою того ж порядку, що і
;
другий доданок
являється при
нескінченно малою того ж порядку, що і
;
другий доданок
 є нескінченно мала вищого порядку, ніж
.
Отже, перший доданок складає головну
частину приросту функції w=f(z).
є нескінченно мала вищого порядку, ніж
.
Отже, перший доданок складає головну
частину приросту функції w=f(z).
Диференціалом
dw
аналітичної
функції w=f(z)
у точці
z називається
головна частина її приросту, тобто
 ,
або
,
або
 ,
тобто похідна функції дорівнює відношенню
диференціала функції до диференціала
незалежної змінної.
,
тобто похідна функції дорівнює відношенню
диференціала функції до диференціала
незалежної змінної.
Зауваження.
Якщо
функція
 аналітична в деякій області D, то функції
u(x;y)
і
v(x;y)
задовольняють диференціальному рівнянню
Лапласа (
аналітична в деякій області D, то функції
u(x;y)
і
v(x;y)
задовольняють диференціальному рівнянню
Лапласа ( ).
).
Дійсно, диференціюючи першу з рівностей Ейлера-Даламбера по y, а другу по x, отримаємо:
 ,
,
 ,
,
звідси
 .
.
Функції u(x;y) і v(x;y) називаються гармонічними функціями.
Приклад 3. Перевірити, чи є функція аналітичною. Знайти її похідну.
○ Знаходимо
дійсну
 і уявну
і уявну
 частини функції:
частини функції:
 .
.
Таким чином, , . Перевіряємо умови Ейлера-Даламбера (1.5):
 ,
,
 ;
;
 ,
,
 .
.
Умови (1.5) виконуються у всіх точках комплексної площини z. Функція диференційовна, отже, аналітична у всіх точках цієї площини. Її похідну знайдемо за однією з формул (1.6), наприклад за першою:
 ,
,
тобто
 .
.
Замітимо, що похідну функції можна знайти, скориставшись означенням похідної (1.4):
 . ●
. ●
Приклад
4.
Знайти аналітичну функцію w=u+iv
за
її заданою дійсною частиною
 .
.
○ Відзначимо,
що функція u
є гармонічною функцією ( ,
,
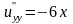 ,
отже,
,
отже,
 ).
).
Для
визначення уявної частини v
скористаємося
умовами Ейлера-Даламбера (1.5).
Оскільки
 ,
то, згідно першій умові,
,
то, згідно першій умові,
 . Звідси, інтегруючи по y,
знаходимо:
. Звідси, інтегруючи по y,
знаходимо:
 .
.
Для
визначення функції
 скористаємося другою умовою
Ейлера-Даламбера. Оскільки
скористаємося другою умовою
Ейлера-Даламбера. Оскільки
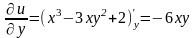 ,
,
 ,
,
то
 .
Звідси
.
Звідси
 і
і
 ,
де C
= const.
Тому
,
де C
= const.
Тому
 .
Знаходимо функцію w=u+iv:
.
Знаходимо функцію w=u+iv:
 ●
●
2. Інтегрування функції комплексної змінної
2.1 Означення, властивості і правила обчислення інтеграла

Нехай у кожній точці деякої гладенької кривої L з початком у точці z0 і кінцем у точці z визначена неперервна функція f(z).
Розіб'ємо криву L на n частин (елементарних дуг) у напрямку від z0 до z точками z1, z2,…,zn-1 (див. рис. 6).
Рис. 6
У кожній
«елементарній дузі» zk-1zk
(k = 1,2,…,n) виберемо довільну точку Ck
і складемо інтегральну суму
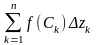 ,
де
,
де
 .
.
Границя
такої інтегральної суми при прямуванні
до нуля довжини найбільшої з елементарних
дуг, якщо вона існує, називається
інтегралом
від
функції f(z) по кривій (по контуру) L
і позначається символом
 .
.
Таким чином,
 (2.1)
(2.1)
Покажемо, що якщо L – гладка крива, а f(z) – неперервна й однозначна функція, то інтеграл (2.1) існує.
Дійсно,
нехай
,
,
 .
Тоді
.
Тоді
 ,
,
 .
.
Тому

= .
.
Обидві суми, що знаходяться в правій частині останньої рівності, є інтегральними сумами для відповідних криволінійних інтегралів.
При
зроблених припущеннях про криву L
і
функцію
f(z)
границі цих сум існують. Тому після
переходу до границі (в останній рівності)
при
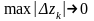 одержимо:
одержимо:
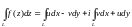 (2.2)
(2.2)
Формула (2.2) показує, що обчислення інтеграла від функції комплексної змінної зводиться до обчислення криволінійних інтегралів від дійсних функцій дійсних змінних.
Формулу (2.2) можна записати в зручному для запам'ятання вигляді:
 (2.3)
(2.3)
Якщо
x=x(t),
y=y(t),
де
 -параметричні
рівняння кривої L,
то
z=z(t)=x(t)+iy(t) називають
комплексним
параметричним рівнянням кривої
L;
формула (2.3) перетвориться у формулу
-параметричні
рівняння кривої L,
то
z=z(t)=x(t)+iy(t) називають
комплексним
параметричним рівнянням кривої
L;
формула (2.3) перетвориться у формулу
 (2.4)
(2.4)
Дійсно, вважаючи z(t) неперервною і диференційовною функцією, одержуємо:

Наведемо основні властивості інтеграла від функції комплексної змінної.



 , a
–
комплексне число.
, a
–
комплексне число. , тобто
при зміні напрямку шляху інтегрування
інтеграл змінює свій знак на протилежний
(в інших позначеннях кривої:
, тобто
при зміні напрямку шляху інтегрування
інтеграл змінює свій знак на протилежний
(в інших позначеннях кривої:
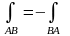 )
.
)
. , де
L=L1+L2,
тобто інтеграл по всьому шляху L
дорівнює
сумі інтегралів по його частинах
L1
і
L2.
, де
L=L1+L2,
тобто інтеграл по всьому шляху L
дорівнює
сумі інтегралів по його частинах
L1
і
L2.Оцінка модуля інтеграла. Якщо
 у
всіх точках кривої L,
то
у
всіх точках кривої L,
то
 ,
де
l –
довжина кривої
L.
,
де
l –
довжина кривої
L.
Дійсно,
 ,
,
де
 -
довжина ламаної z0z1z2…zn,
вписаної в криву
L.
-
довжина ламаної z0z1z2…zn,
вписаної в криву
L.
Всі наведені властивості інтеграла функції комплексної змінної безпосередньо випливають з його означення (2.1) і подання (2.2).
Приклад
7.
Обчислити
 ,
де L
– півколо
,
,
де L
– півколо
,
 (див. рис.7).
(див. рис.7).
 Розв’язання:
Використовуючи формулу (2.3), маємо:
Розв’язання:
Використовуючи формулу (2.3), маємо:
○
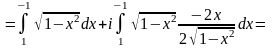
 .
.
Рис. 7
Використовуючи
формулу (2.4), маємо
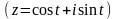 :
:

 ●
●
