Елементи теорії функцій комплексної змінної

1. Функції комплексної змінної.

1.1. Основні поняття

Нехай дані дві множини D і E, елементами яких є комплексні числа. Числа 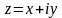множини D будемо зображати точками комплексної площини z, а числа множини E – точками комплексної площини w.

Я кщо кожному числу (точці) за деяким правилом поставлено у відповідність певне число (точка) , то кажуть, що на множині визначена однозначна функція комплексної змінної , що відображає множину D у множину E (див. рис. 1).

Якщо кожному відповідає декілька значень , то функція

називається багатозначна.

Рис.1

Множина D називається областю визначення функції ; множина E₁ всіх значень w, що f(z) приймає на E, називається областю значень цієї функції (якщо ж кожна точка множини E є значенням функції, то E – область значень функції; у цьому випадку функція f відображає D на E).

Далі, як правило, будемо розглядати такі функції , для яких множини D і E₁ є областями. Областю комплексної площини називається множини точок площини, що мають властивості відкритості і зв’язності.

Функцію можна записати у вигляді: , тобто , де , , .

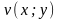Функцію , при цьому, називають дійсною частиною функції , а – уявною.

Таким чином, задання функції комплексної змінної рівносильне заданню двох функцій двох дійсних змінних.

Приклад 1. Знайти дійсну і уявну частини функції .

○ Функцію можна записати у вигляді , тобто .

Звідси випливає: , . ●

1.2 Границя і неперервність функції комплексної змінної

Нехай однозначна функція визначена в деякому околі точки z₀, крім, можливо, самої точки z₀. Під -околом точки z₀ комплексної площини розуміють внутрішність круга радіуса з центром у точці z₀.

Число w₀ називається границею функції в точці z₀ (чи при 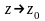), якщо для будь-якого додатного 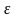знайдеться таке додатне число , що для всіх 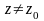, які задовольняють нерівність , виконується нерівність .

Записують: . Це означення коротше можна записати так:

.

З означення випливає, що якщо границя w₀ існує, то існують і границ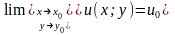і і .

Справедливе обернене твердження.

Теореми про арифметичні властивості границь для функції однієї (чи декількох) дійсних змінних залишаються справедливими і для функції комплексної змінної. Так, якщо функції і мають границі в точці , то:

1. , де , - постійні;

2. ;

3. , якщо .

Нехай функція визначена в точці 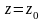і у деякому її околі. Функція називається неперервною в точці , якщо .

Означення неперервності можна сформулювати так: функція неперервна в точці , якщо нескінченно малому приросту аргументу відповідає нескінченно малий приріст функції: .

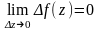Функція неперервна в області , якщо вона неперервна в кожній точці цієї області.

Модуль неперервної функції комплексної змінної має ті ж властивості, що і неперервна функція дійсної змінної.