Определение степени соответствия теоретического распределения данным эксперимента
При подборе теоретической кривой распределения между нею и статистическим распределением неизбежны некоторые расхождения. При этом необходимо знать, объясняются эти расхождения только случайными обстоятельствами, связанными с ограниченным числом опытных данных, или они являются существенными и связаны с тем, что подобранная кривая плохо выравнивает данное статистическое распределение.
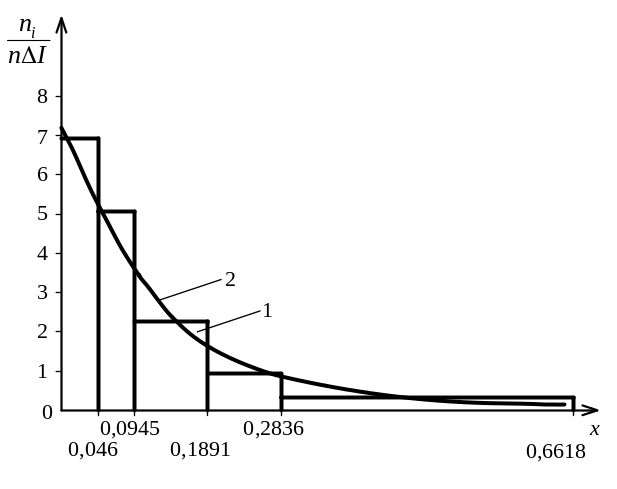
Рис. 8. Гистограмма (1) и выравнивающая кривая (2) экспоненциального распределения
Степень соответствия между выдвинутой гипотезой со статистическим материалом устанавливается с помощью критериев согласия.
Наиболее распространенным является критерий К. Пирсона , величина которого рассчитывается по формуле
,
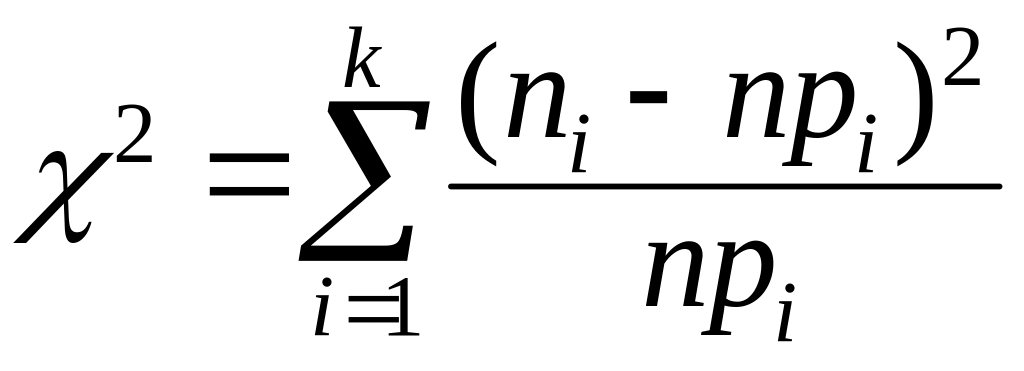(4)
где k ― число интервалов группирования случайной величины; ni ― число значений случайной величины в i-м интервале; n ― общее число полученных значений случайной величины; p ― теоретическая вероятность попадания случайной величины в i-й интервал.
Теоретическая вероятность попадания случайной величины X в i-й интервал равна приращению функции распределения на этом интервале:
.
(5)
Функция экспоненциального распределения описывается формулой
,
поэтому формулу (5) можно представить как
.
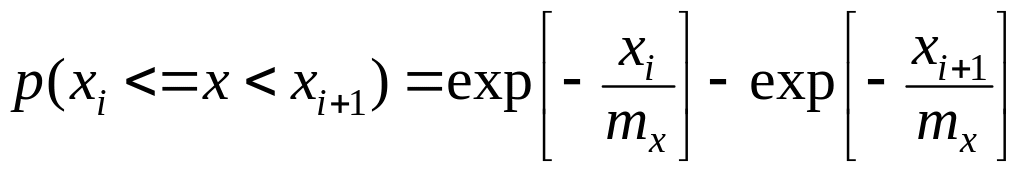Значения
приведены в таблице 6.
Таблица 6
-
Границы интервалов
0
-
0,046
0,2843
0,0945
0,2127
0,1891
0,2500
0,2836
0,1258
0,6618
0,1191
По формуле (4) и данным таблиц 3 и 6 находим значение критерия согласия Пирсона =1,53.
Число степеней свободы распределения определяется по формуле
r=k-s,
где k ― число интервалов группирования случайной величины; s ― число независимых условий (связей), налагаемых на частоты .
Для экспоненциального закона распределения s = 2, следовательно, число степеней свободы в рассматриваемом случае составляет r = 5 – 2 = 3.
Пользуясь таблицей значений вероятностей для критерия , находим вероятность того, что эмпирическое распределение подчиняется экспоненциальному закону. Если получаемая вероятность составляет более 10 %, то обычно считается, что экспериментальные данные не противоречат принятому теоретическому закону распределения случайной величины.
Для =1,53 и r =3 значение вероятности находится в пределах между 50 и 70 %, значит, предположение о том, что экспериментальные данные подчиняются экспоненциальному закону распределения, является верным.
7. Заключение о надежности объекта
В результате обработки исходной статистической информации о надежности объекта, представленной в виде статистического ряда (см. табл. 1), установлены:
― средняя
наработка на отказ объекта
0,138;
― вид закона распределения случайной величины x
;
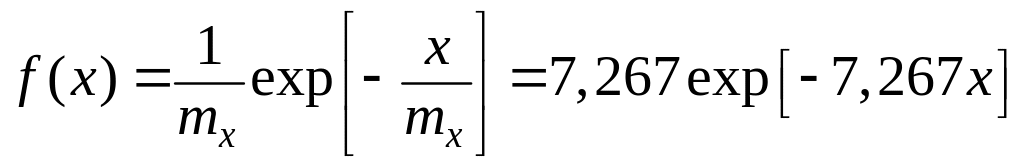― аналитическое выражение для определения вероятности безотказной работы объекта
.
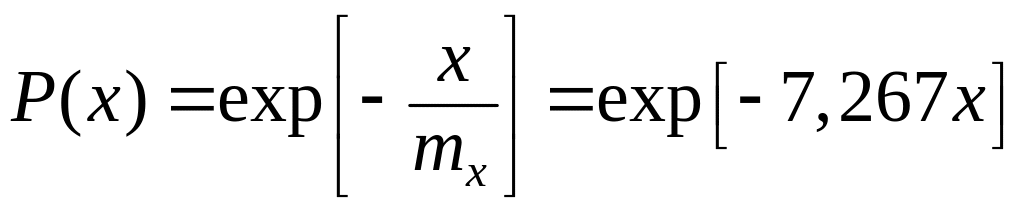Итак, установлено, что исходные экспериментальные данные подчиняются экспоненциальному закону распределения. Экспоненциальному закону распределения подчиняются случайные значения времени работы между отказами или до отказа объектов, для которых характерны внезапные отказы.