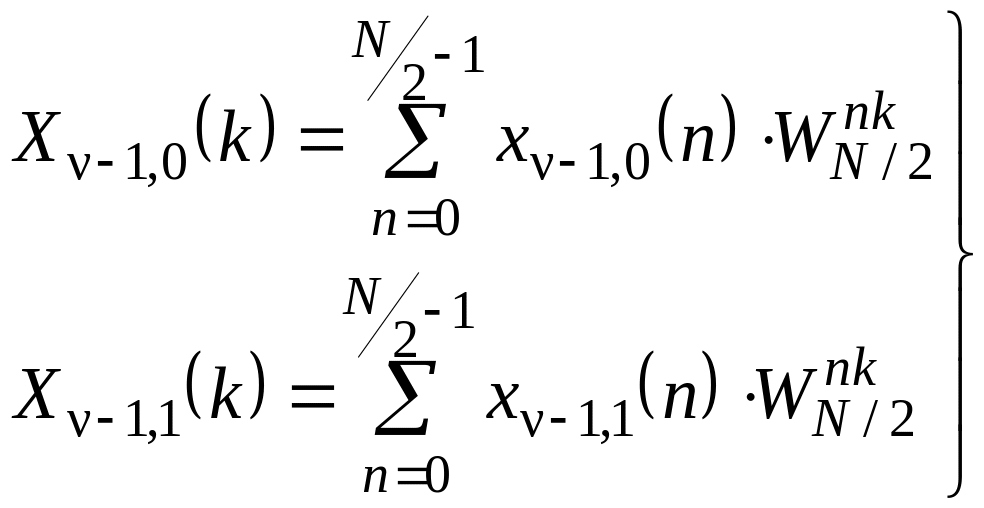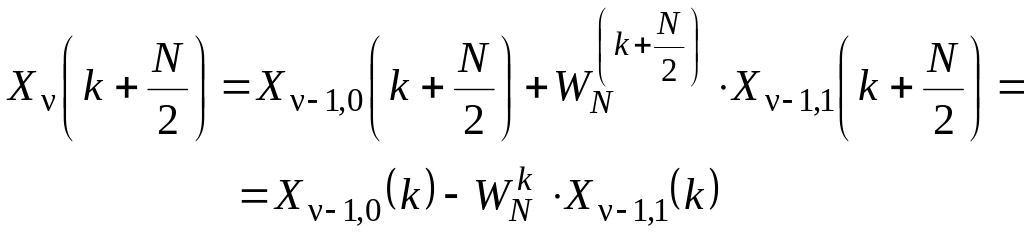Тема 6. Быстрое преобразование Фурье (бпф)

Основы алгоритмов БПФ

ДПФ			(1)
ОДПФ			(2)
	где		(3)

Непосредственное вычисление ДПФ при комплексных требует для каждого значения (N-1) умноженной на (N-1) сложений комплексных чисел, или 4(N-1) умножений и (2N-2) сложений действительных чисел.

Для всех N значений k требуется примерно умножений и сложений комплексных чисел.

При больших N (100-1000) практическое применение прямого алгоритма невозможно или экономически невыгодно.

БПФ называют набор алгоритмов, которые существенно уменьшают вычислительную сложность ДПФ. Основная идея этих алгоритмов: разделение исходной N-точечной последовательности на несколько более коротких, например на два длинною . Затем вычисляются их ДПФ и из них конструируются ДПФ исходной последовательности.

Для двух -точечных последовательностей требуется умножений и сложений комплексных чисел, т.е. число операций уменьшается примерно в два раза. Аналогично, вместо вычисления - точечной ДПФ можно разбить последовательность на две - точечные последовательности, что ещё более уменьшит число операций.

Если , и целое, то процесс уменьшения размера ДПФ продолжается до тех пор пока не останутся 2х точечные ДПФ, при этом общее число этапов равно алгоритмов, а число арифметических операций , т.е. в раз меньше, чем по прямой формуле.

N = 1000	по прямой формуле	≈ 106 операций
	БПФ	≈ 104 операций
	Выигрыш	в 100 раз

Алгоритм быстрого преобразования Фурье с прореживанием

Пусть .

Есть длина последовательности не кратна степени 2, то её можно дополнить нулями.

Исходная последовательность: .

Разобьём её на две части, состоящие из чётных и нечётных элементов.

(4)

(5)

Так как , то

(6)

(6а)

должно быть определено для N точек,

а в (6а) и должны быть определены для .

Доопределим выражение (6) для значений: , учитывая, что - точечные ДПФ в (6а) периодические.

(7)

(т.к. )

Формулы (6) и (7) дают алгоритм вычисления N-точечного ДПФ через -точечные.

Этот алгоритм можно представить направленным графом, имеющим вид бабочки:

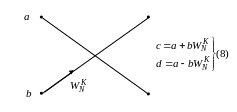
(6) и (7)

Можно продолжить и далее и выразить -точечные ДПФ через -точечные:

	(9)
	(10)

Процесс уменьшения ДПФ продолжается до тех пот, пока на -ом шаге не окажутся только двухточечные ДПФ.

(11)

Пример:

; .

1)

2) Разбиваем последовательность на чётные и нечётные элементы:

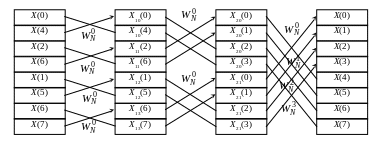
При использовании алгоритма ДПФ с прореживанием по времени производится перестановка входной последовательности в соответствии с реверсивным (инверсным) двоичным представлением номера элемента.

0	000		000	0
1	001		100	4
2	010		010	2
3	011		110	6
4	100		001	1
5	101		101	5
6	110		011	3
7	111		111	7

Алгоритм ДПФ с прореживаем по частоте

Исходная последовательность делиться на части:

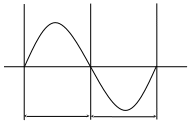
Этот алгоритм можно представить направленным графом, имеющим вид бабочки:

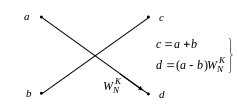
Пример:

;

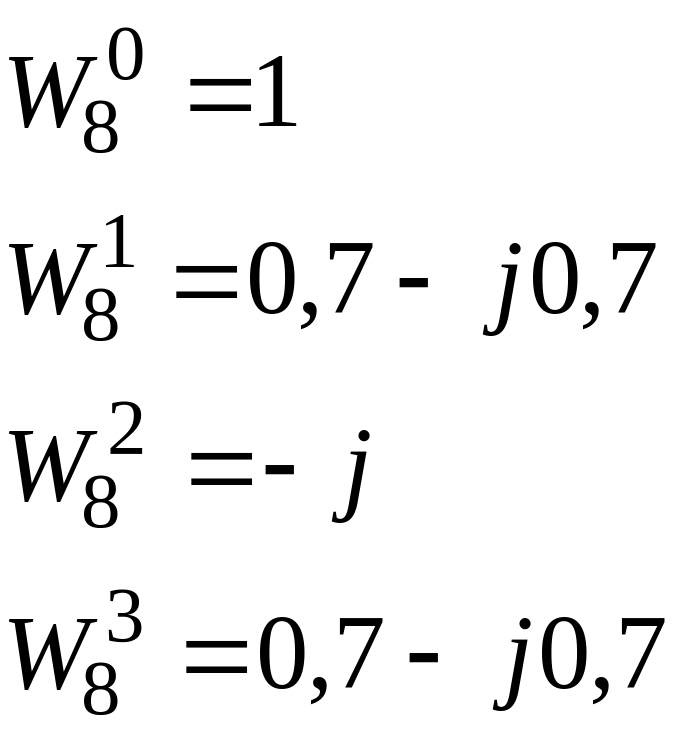
0	28
1
2
1
1
1
1
1

Рассмотренные алгоритмы ДПФ называются алгоритмами Кули-Тьюки по основанию два. По вычислительной эффективности они одинаковы. Существуют более эффективные алгоритмы ДПФ.

Применение БПФ для вычисления обратного дискретного преобразования Фурье (ОДПФ).

ОДПФ вычисляется по формуле:

(12)

Обозначим:

комплексно-сопряженное с

комплексно-сопряженное с

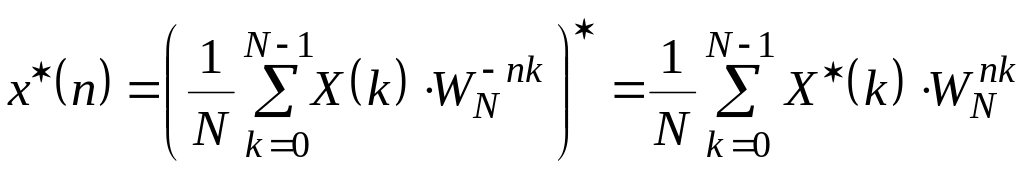(13)

Можно заметить, что сумма правой части в выражении (13) – это прямое ДПФ последовательности , следовательно, она может быть вычислена при помощи рассмотренных алгоритмов БПФ.

(14)

Для исходной последовательности:

1. Нужно найти комплексно-сопряжённую последовательность

2. Для найденной комплексно-сопряжённой последовательности нужно вычислить БПФ.

3. Найти комплексно-сопряжённую последовательность с результатом БПФ.

4. Поделить результат на N.

Задачи:

1. Вычислить БПФ с прореживанием по времени.

При

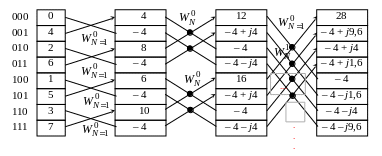
При N=4

ОБПФ

сопряжение перестановка /N=/4

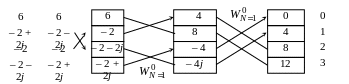
2. Вычислить БПФ с использованием прореживания по частоте.

Пояснение к перестановкам

0	000		000	0		28	28
1	001		100	4		– 4	– 4 + j9,6
2	010		010	2		– 4 + j4	– 4 + j4
3	011		110	6		– 4 – j4	– 4 + j1,6
4	100		001	1		– 4 + j9,6	– 4
5	101		101	5		– 4 – j1,6	– 4 – j1,6
6	110		011	3		– 4 + j1,6	– 4 – j4
7	111		111	7		– 4 – j9,6	– 4 – j9,6