
- •Через любые две точки можно провести прямую, и притом только одну.
- •Две прямые либо имеют только одну общую точку, либо не имеют общих точек.
- •3. Провешивание прямой на местности
- •6. Угол
- •7. Равенство геометрических фигур
- •8. Сравнение отрезков
- •9. Сравнение углов
- •10. Длина отрезка
- •11. Единицы измерения отрезков. Измерительные инструменты
- •12. Градусная мера угла
- •13. Измерение углов на местности
- •14. Смежные и вертикальные углы
- •15. Перпендикулярные прямые
- •16. Треугольник
- •17. Первый признак равенства треугольников
- •18. Перпендикуляр к прямой
- •19. Медианы, биссектрисы и высоты треугольника
17. Первый признак равенства треугольников
В математике каждое утверждение, справедливость которого устанавливается путем рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы.
Теорема:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Д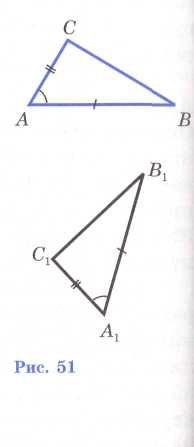 оказательство:
оказательство:
Рассмотрим треугольники ABC и ∆А1В1С1 у которых
АВ=А1В1, АС=А1С1, углы A и A1 равны (рис. 51).
Докажем, что ∆АВС = ∆А1В1С1.
Так как А=A1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ =А1В1, АС =А1С1, то сторона АВ совместится со стороной А1В1, а сторона АС — со стороной А1С1 в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны. Теорема доказана.
Доказанная теорема выражает признак (равенство у треугольников двух сторон и угла между ними), по которому можно сделать вывод о равенстве треугольников. Он называется первым признаком равенства треугольников.
18. Перпендикуляр к прямой
Р ассмотрим
прямую а
и
точку А,
не
лежащую на этой прямой (рис. 55). Соединим
точку А отрезком с точкой Н
прямой
а.
Отрезок
АН
называется
перпендикуляром,
проведенным из точки А
к
прямой а,
если
прямые АН и а
перпендикулярны.
Точка Н
называется
основанием
перпендикуляра.
ассмотрим
прямую а
и
точку А,
не
лежащую на этой прямой (рис. 55). Соединим
точку А отрезком с точкой Н
прямой
а.
Отрезок
АН
называется
перпендикуляром,
проведенным из точки А
к
прямой а,
если
прямые АН и а
перпендикулярны.
Точка Н
называется
основанием
перпендикуляра.
Теорема
И з
точки, не лежащей на прямой, можно
провести перпендикуляр к этой прямой,
и притом только один.
з
точки, не лежащей на прямой, можно
провести перпендикуляр к этой прямой,
и притом только один.
Доказательство
Пусть А — точка, не лежащая на прямой ВС (рис. 56, а). Докажем сначала, что из точки А можно провести перпендикуляр к прямой ВС.
Отложим от луча ВС угол МВС, равный углу ABC, как показано на рисунке 56, а. Так как углы ABC и МВС равны, то первый из них можно наложить на второй так, что стороны ВА и ВС первого угла совместятся со сторонами ВМ и ВС второго угла. Наглядно это наложение можно представить себе как перегибание рисунка по прямой ВС. При этом точка А наложится на некоторую точку А1 луча ВМ (рис. 56, б). Обозначим буквой Н точку пересечения прямых АА1 и ВС. Отрезок АН и есть искомый перпендикуляр к прямой ВС. В самом деле, при указанном наложении (перегибании рисунка) луч на совмещается с лучом НА1, поэтому угол 1 совмещается с углом 2. Следовательно, l=2. Но углы 1 и 2 — смежные, значит, каждый из них прямой. Итак, АНВС.
Докажем теперь, что из точки А можно провести только один перпендикуляр к прямой ВС.
Е
 сли
предположить, что через точку А
можно
провести еще один перпендикуляр АН1
к
прямой ВС,
то
получим, что две прямые АН
и
AH1
перпендикулярные
к прямой ВС,
пересекаются
(рис. 57). Но в п. 12 было доказано, что это
невозможно. Итак, из точки А
можно
провести только один перпендикуляр к
прямой ВС.
Теорема
доказана.
сли
предположить, что через точку А
можно
провести еще один перпендикуляр АН1
к
прямой ВС,
то
получим, что две прямые АН
и
AH1
перпендикулярные
к прямой ВС,
пересекаются
(рис. 57). Но в п. 12 было доказано, что это
невозможно. Итак, из точки А
можно
провести только один перпендикуляр к
прямой ВС.
Теорема
доказана.
Д ля
проведения на чертеже перпендикуляра
из точки к прямой используют чертежный
угольник (рис. 58).
ля
проведения на чертеже перпендикуляра
из точки к прямой используют чертежный
угольник (рис. 58).
