
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Энергетический институт
Кафедра электроснабжения промышленных предприятий
СИНТЕЗ АНАЛОГОВЫХ ФИЛЬТРОВ С ЗАДАННЫМИ
ХАРАКТЕРИСТИКАМИ И АНАЛИЗ ИХ РАБОТЫ
Наименование лабораторной работы
Отчет по лабораторной работе № 3
по курсу «Дополнительные главы математики»
Наименование учебной дисциплины
Вариант №13
Выполнил студентка гр. 5АМ24 ________ Е.В. Ивашова
Подпись Дата И.О.Фамилия
Проверил доцент______ _______ _________ А.С. Глазырин
должность Подпись Дата И.О.Фамилия
Томск – 2012
Содержание
Цели работы:
1. Научиться выводить системы обыкновенных дифференциальных уравнений (ОДУ), описывающих динамику элементов автоматических устройств (ЭАУ), на примере нагруженного LCR-фильтра низких частот (ФНЧ).
2. Научиться определять переходные функции ЭАУ с применением прямого и обратного преобразований Лапласа на примере нагруженного LCR-ФНЧ.
3. Научиться определять показатели качества по переходным функциям ЭАУ на примере нагруженного LCR-ФНЧ с применением различных методов решения нелинейных уравнений.
4. Научиться выводить аналитические выражения для частотных характеристик ЭАУ на примере нагруженного LCR-ФНЧ.
5. Научиться определять показатели качества по частотным характеристикам ЭАУ на примере нагруженного LCR-ФНЧ.
6. Закрепить полученные знания и умения – исследовать самостоятельно нагруженный LCR-ФВЧ (фильтр верхних частот).
Таблица 1. Исходные данные
Вариант |
L, мГн
|
C, мкФ
|
Метод решения нелинейных уравнений |
13 |
500 |
600 |
Метод секущих |
Часть 1:
Анализ характеристик фильтра
Исходя из данных варианта, рассчитаем основные характеристики фильтра низких частот (ФНЧ) второго порядка представленном на рис.1

Рисунок 1. - Аналоговый ФНЧ второго порядка
Передаточное уравнение для ФНЧ имеет вид (1)
На первом этапе необходимо составить систему дифференциальных уравнений, описывающих состояние ФНЧ. На вход ФНЧ подаётся гармонический сигнал. Будем использовать следующие обозначения переменных:
UВХ (t) - входное напряжение;
UВых (t) - выходное напряжение;
iL (t) - ток катушки индуктивности;
iC (t) - ток конденсатора;
iH (t) - ток нагрузки.
По второму закону Кирхгофа входное напряжение уравновешивается
как
 (1)
(1)
Согласно первому закону Кирхгофа ток катушки индуктивности iL расщепляется на ток конденсатора iC и ток нагрузки iH :
 (2)
(2)
Известно, что ток конденсатора определяется как
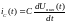 (3)
(3)
а ток нагрузки по закону Ома выразим как
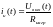 (4)
(4)
Система дифференциальных уравнений, описывающих состояние ФНЧ с учётом (1) - (4), выглядит следующим образом:
 (5)
(5)
Применим к выражению (5) прямое преобразование Лапласа, получим систему алгебраических уравнений в изображениях и проведём алгебраические преобразования:
 (6)
(6)
где s - оператор Лапласа.
Подставим второе уравнение системы (6) в первое и проведём алгебраические преобразования
 (7)
(7)
Операторной передаточной функцией ФНЧ W (s) называется отношение изображение выходного сигнала UBыX (s) ко входному UBX (s):
 (8)
(8)
С учётом (7) и (8) запишем выражение для операторной передаточной функции ФНЧ:
 (9)
(9)
Запишем выражение для выходного напряжения:
 (10)
(10)
где
 - операторная форма входного напряжения,
прикладываемого ступенчато
при коммутации ключа
- операторная форма входного напряжения,
прикладываемого ступенчато
при коммутации ключа
Упростим в MathCAD выражение (10) с применением оператора упрощения выражений simplify для Rнагр = 1000 • R
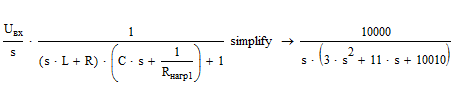
К выражению, полученному в результате упрощения, применим обратное преобразование Лапласа с учётом нулевых начальных условий (до коммутации токи и напряжения ФНЧ равны нулю)
Получаем переходную функцию ФНЧ в ненагруженном режиме

Аналогично получим и для остальных:
В ненагруженном режиме: 
В нормальном режиме:
В нагруженном режиме:
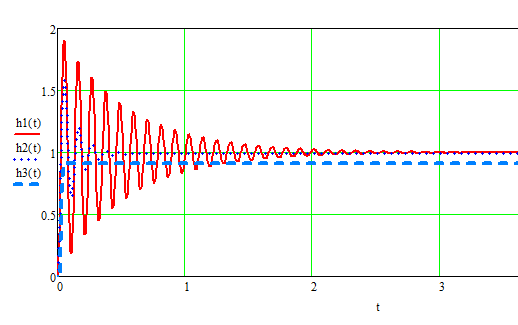
Рисунок 2. - Переходные характеристики фильтра с различными нагрузками
Найдём величину перерегулирования, для этого определим первую точку экстремума, определим производную по h(t):


Рисунок 3.- Зона допустимых отклонений
Найдём время завершения переходного процесса, последний переход функции через нуль, определив начальное приближение времени графически.


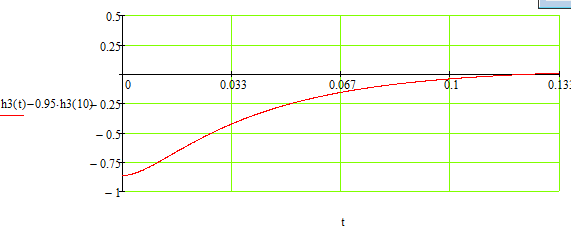
Рисунок 4. - Время завершения переходного процесса

Рисунок 5.- Метод секущих
Для более точного решения воспользуемся методом секущих.
Если итерации Хк и Хк+1 расположены достаточно близко друг к другу, то в методе Ньютона можно заменить производную первой конечной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей.
Для начала итерационного процесса необходимо задать два начальных приближения х0 и х1. Скорость сходимости метода секущих несколько ниже, чем метода касательных, однако он не требует вычисления производной левой части уравнения. Блок схема алгоритма метода секущих приведена на рисунке ниже.

Рисунок 6.- Алгиритм метода секущих
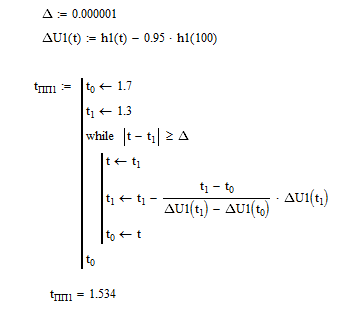


ПОСТРОЕНИЕ И АНАЛИЗ ЧАСТОТНЫХ ХАРАКТЕРИСТИК
В MATHCAD
Заменим в (9) оператор Лапласа s на комплексную переменную jw

Воспользовавшись процедурой избавления от мнимой единицы получим
Составим программу в MathCAD для определения корня нелинейного уравнения методом секущих


- вещественно-частотная характеристика (ВЧХ) ФНЧ

мнимочастотная характеристика (МЧХ) ФНЧ,
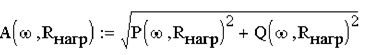
- амплитудно-частотная характеристика (АЧХ) ФНЧ

- фазочастотная характеристика (ФЧХ) ФНЧ
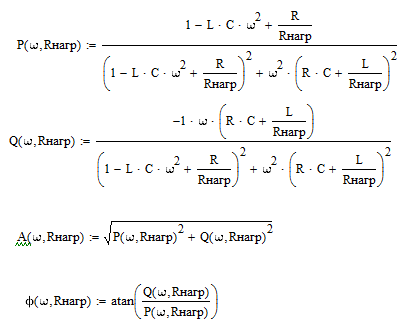
Для нахождения резонансной частоты ФНЧ необходимо АЧХ продифференцировать по частоте ю и ввести результат в соответствующую функцию

Приравняем производную к нулю и решим нелинейное уравнение с помощью процедуры solve
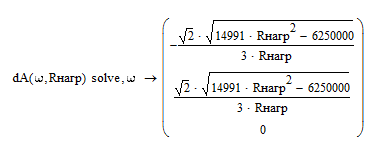
Отбросим первый и третий полученные корни, а второй корень представим в виде функции, затем определим резонансные частоты при трёх значениях сопротивления нагрузки


Рисунок 7.- Амплитудно-частотные характеристики ФНЧ при разных сопротивлениях нагрузки.
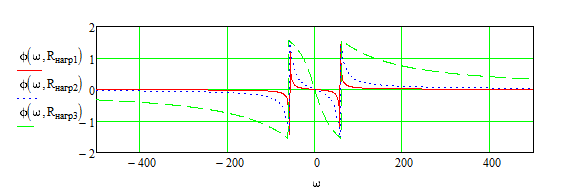
Рисунок 8.- Фазочастотные характеристики (ФЧХ) ФВЧ при разных сопротивлениях нагрузки
Если повышать частоту входного сигнала ФНЧ, начиная от резонансной, то амплитуда выходного напряжения при некоторой частоте снизится в
V2 раз, по сравнению с амплитудой, при частоте, стремящейся к нулю. Такая частота определяет полосу пропускания ФНЧ. Определим полосу пропускания ФНЧ при ненагруженном режиме, решив нелинейное уравнение с помощью процедур solve. Результат представим в формате float (с плавающей точкой), взяв первые шесть значащих цифр результата.

Истинным решением будет первый корень, так как он является действительным положительным числом.
Определим полосу пропускания рассматриваемого фильтра при ненагруженном режиме, решив нелинейное уравнение при помощи метода секущих:
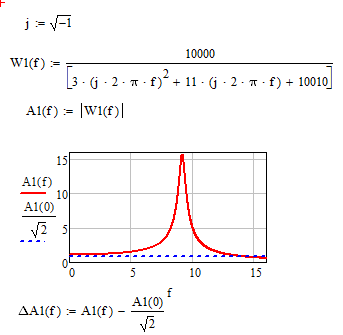
Рисунок 9.– АЧХ ненагруженного режима ФВЧ
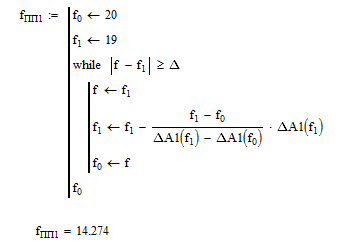
Аналогичным образом определяем полосу пропускания фильтра для нагруженного и нормального режимов:

Рисунок 10 – АЧХ нормального режима ФВЧ


Рисунок 11 – АЧХ нагруженного режима ФВЧ
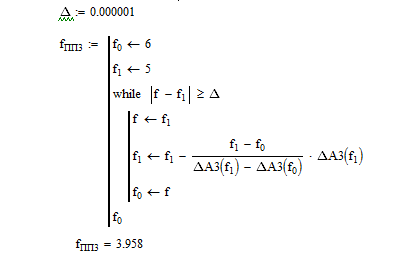
Для расчёта резонансной частоты, исходя из графика






Таблица1 – Результаты исследований динамики ФВЧ по частотным характеристикам
Показатель |
Сопротивление нагрузки |
||
|
|
|
|
Резонансная частота
|
9,184 |
8,993 |
0,025 |
Полоса пропускания
|
14,274 |
14,085 |
3,958 |
Время переходно- го процесса, с |
1,534 |
0,29 |
0,125 |

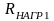 =1000*R
=1000*R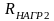 =100*R
=100*R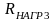 =10*R
=10*R , рад/с ;
, рад/с ;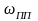 ,
рад/с
,
рад/с