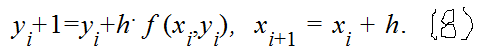17. Интерполяция функции полиномами Ньютона

Интерполяция функции , заданной , где заключается в нахождении полинома , значения которого в узловых точках совпадают со значениями , позволяющего найти значения в промежутках между узлами.

Существует множество разностных методов интерполяции, однако наиболее распространен метод Ньютона для интерполирования вперед, известный также как метод Ньютона-Грегори. Интерполяционный многочлен для метода разделенных разностей имеет вид

_{Коэффициенты} определяются из условия Лагранжа следующим образом: При

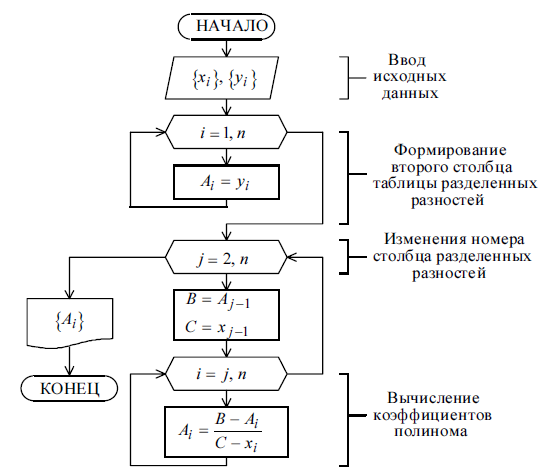
_{Блок-схема алгоритма вычисления коэффициентов полинома Ньютона}

_{При программной реализации полином Ньютона удобнее вычислять по формуле Горнера}

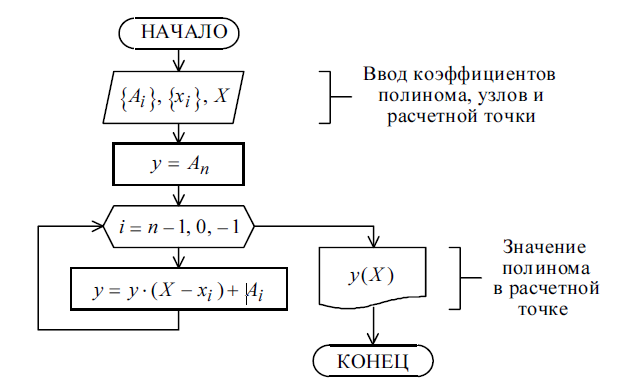
_{Блок-схема алгоритма вычисления коэффициентов полинома по схеме Горнера}

Интерполяция – способ приближенного вычисления значения величины, находящегося между двумя известными значениями.

Аппроксимация – замена одних математических объектов другими, в том или ином смысле близкими к исходным.

Полином - многочлен

18. Интерполяция функции кубическими сплайнами

Интерполяция функции , заданной , где заключается в нахождении полинома , значения которого в узловых точках совпадают со значениями , позволяющего найти значения в промежутках между узлами.

Е сли в качестве функции выбрать полином, то степень полинома должна быть не выше третьей. Этот полином называют кубическим сплайном.

В отличие от полиномиальной интерполяции, когда вся аппроксимируемая зависимость описывается одним полиномом, при сплайновой интерполяции на каждом интервале строится отдельный полином третьей степени со своими коэффициентами.

Интерполяция – способ приближенного вычисления значения величины, находящегося между двумя известными значениями.

Аппроксимация – замена одних математических объектов другими, в том или ином смысле близкими к исходным.

Полином – многочлен

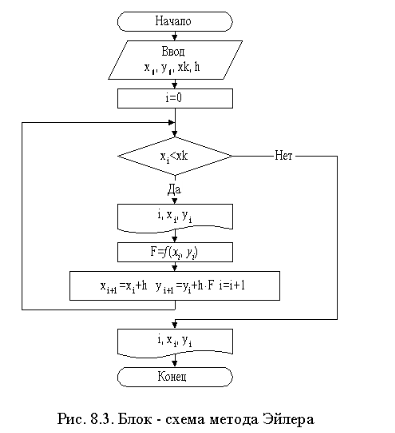
19. Метод Эйлера для решения дифференциальных уравнений.

Простейшим из численных методов решения дифференциальных уравнений является метод Эйлера. Это один из самых старых и широко известных методов. Метод Эйлера является сравнительно грубым методом решения дифференциальных уравнений, однако идеи, положенные в его основу, являются, по существу, исходными для очень широкого класса численных методов.

Пусть требуется найти приближенное решение дифференциального уравнения первого порядка

y^/ = f (x,y), (1) с начальным условием y(x0)=y0, (2) т.е. необходимо решить задачу Коши.

В окрестности точки x0 функцию y(x) разложим в ряд Тейлора :

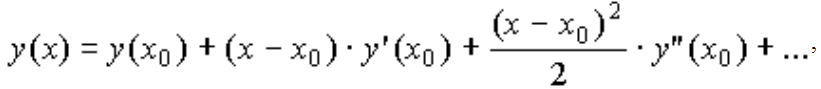(3)

который можно применить для приближенного определения искомой функции y(x). В точке x0+h при малых значениях h можно ограничиться двумя членами ряда (3), тогда, 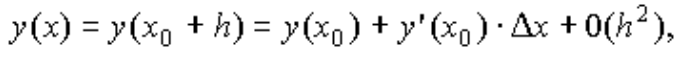(4)

где 0(h²) - бесконечно малая величина порядка h². Заменим производную y^/(x0), входящую в формулу (3), на правую часть уравнения (1) :

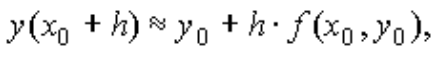(5)

Теперь приближенное решение в точке x1=x0+h можно вновь рассматривать как начальное условие и по формуле (5) найти значение искомой функции в следующей точке x2=x1+h. В результате получен простейший алгоритм решения задачи Коши, который называется методом Эйлера или методом ломаных.

Метод Эйлера можно представить в виде последовательного применения формул: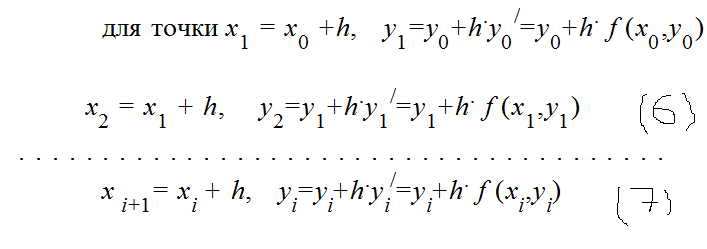 Таким образом, формула Эйлера в общем случае имеет вид: