12. Блок-схема алгоритма метода дихотомии для решения нелинейных уравнений.

Во многих научных и инженерных задачах возникает необходимость решения уравнений вида где f – заданная функция;

x – неизвестная переменная;

Считаем, что в уравнении (2.1) отделение корней проведено и на отрезке [a,b] расположен только один корень (рис. 2.2).

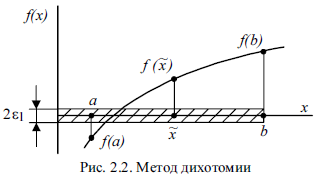
Суть метода дихотомии заключается в следующем [5].

Делят интервал [a,b] пополам и находят

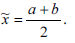
Корень будет находиться в той половине отрезка, на концах которой функция f (x) имеет разные знаки (в нашем случае это интервал

Следовательно, для следующего шага уточнения корня точку b нужно переместить в середину отрезка, т.е. положить , и продолжить процесс до тех пор, пока не будет выполняться условие

Следует учитывать, что вблизи корня значения 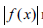могут оказаться настолько малыми, что будут сравнимы с погрешностью вычисления. В этом случае говорят о попадании в так называемую полосу шума , которую следует задать, и прекратить процесс при попадании в нее.

Заметим, что точка а всегда остается слева от корня, поэтому знак

функции в этой точке можно определять один раз и сравнивать знак функции в средней точке, т.е. знак на совпадение или отличие от знака f (a).

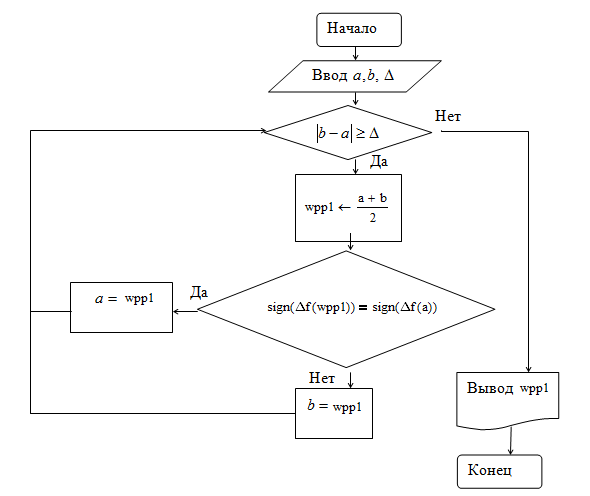
Алгоритм метода дихотомии приведен на рис. 2.3. Он состоит из

следующих этапов:

1. Ввод интервала [a,b], требуемой погрешности вычисления корня ε , полосы шума .

2. Нахождение средней точки интервала:

3. Проверка условия 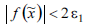и прекращение итерационного процесса (переход к п. 8) в случае его выполнения.

4. Определение знака функции f (x) в средней точке 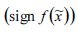и в точке их сравнение.

5. В случае совпадения знаков перенос точки a в точку , в противном случае перенос точки b в точку

6. Проверка условия (2.4) и прекращение итерационного процесса

(переход к п. 8) в случае его выполнения.

7. В противном случае возвращение к п. 2 и продолжение вычислений.

8. Вывод уточненного значения корня

Преимуществами метода дихотомии являются его простота, надежность, сходимость к простому корню для любых, в т.ч. недифференцируемых функций [2]. К его недостаткам следует отнести относительно невысокую скорость сходимости и необходимость предварительного определения интервала, на котором функция меняет знак. Метод применяется главным

образом в тех случаях, когда требуется высокая надежность счета, а скорость сходимости малосущественна.

Конец

Вывод

Ввод

Начало

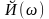
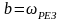
Нет

Да

Да

Нет

13. Блок-схема алгоритма метода касательных (метода Ньютона) для решения нелинейных уравнений

Предположим, что функция 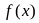непрерывна и дифференцируема на рассматриваемом интервале и, кроме того, графическим или табличным методом определено начальное приближение к корню 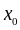(рис. 1).

В точке 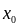вычисляют значение 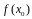и производную 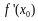. Следующее приближение к корню определяют в точке , где касательная к функции 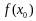, проведенная в точке 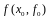, пересекает ось абсцисс. Считая точку в качестве начальной, процесс продолжают до тех пор, пока не выполнится условие .

В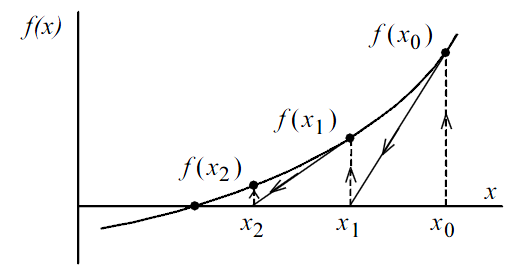 общем виде для 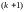-го шага:

Рисунок 1.

Метод ньютона

Графически этот процесс означает замену на каждой итерации графика 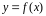касательной к нему.

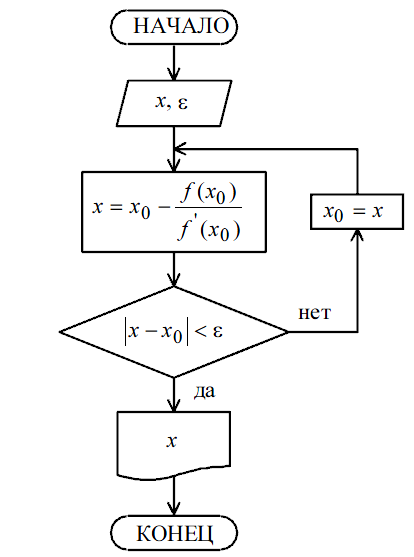
 ввод исходных данных

• Определение корня