Запись и чтение текстовых файлов

Текстовые файлы данных отличаются от бинарных прежде всего тем, что инфор­мация в них содержится в виде закодированных текстовых символов, то есть в символьном виде. Отсюда и название этих файлов. В число записываемых сим­волов входят и управляющие символы, такие как символы окончания строки, пе­ревода каретки, абзаца и др. Поэтому в текстовые файлы записываются те дан­ные, которые образуют сформированный текстовый фрагмент.

Текстовые файлы пригодны и для записи чисел, представленных в виде симво­лов. В этой книге уже шла речь о символьном представлении чисел в MATLAB, когда мы рассказывали, как производится вывод чисел в командное окно. Напом­ним, что в MATLAB существуют такие форматы символьного представления чи­сел: Short, Short Е, Short G, Long, Long E, Long G, Hex, Bank, Plus и Rational.

Остановимся прежде всего на записи и чтении числовых данных. Запись данных в текстовый файл осуществляется с помощью функции fprintf. Обращаться к ней следует таким образом:

Fprintf('<имя_файла>'.'строка_управляющих_символов',<ПЗВ>)

Здесь <имя_файла> — имя файла, в который записываются данные; <ПЗВ> — пере­чень записываемых величин (они должны быть заданы (определены) до откры­тия файла, предназначенного для записи). Строка управляющих символов (она должна быть помещена между апострофами) содержит информацию о том, в ка­ком формате будут записываться данные, указанные в <ПЗВ>. Она может содер­жать помимо управляющих обычные символы. В этом случае символы будут по­мещены между записываемыми данными. К управляющим символам относятся следующие:

• %f — спецификатор, означающий, что очередная переменная, подлежащая за­писи в файл, будет представлена как действительное число в формате с фикси­рованной десятичной точкой (между символами X и f могут быть записаны два целых числа и разделяющая их точка; первое число задает количество символов для записи числа, второе — количество символов после десятичной точки);

• %g — спецификатор, осуществляющий запись числа в формате с плавающей десятичной точкой;

• %s — спецификатор, который осуществляет запись очередной символьной пе­ременной;

• управляющие последовательности символов, имеющие следующие значения:

• \n — конец строки, перевести каретку на следующую строку;

• \t — вставить горизонтальную табуляцию;

• \r — перевести каретку на начало строки;

• \b — возвратиться на один символ;

• \f — перейти к новой странице;

• \” или” — поставить знак апострофа;

• %%— поставить знак процента.

Приведем несколько примеров. Рассмотрим вначале запись вектора. Сформиру­ем вектор из четырех элементов.

» V = [pi. 1.457е-17. -0.312567. 5.089е4]

V = 3.1416е+000 1.4570е-017 -3.1257е-001 5.0890е+004

Запишем этот вектор в текстовый файл в формате с фиксированной десятичной точкой.

FT=fopen('Textl.txt'.'w') fprintf(FT.'%f'.V);

fclose(FT)

Результат записи теперь можно просмотреть, вызвав файл Textl.txt с помощью текстового редактора Блокнот (рис. 3.4).

Рис.3.4.Компоненты вектора в текстовом файле Text1.txt

Как видим, все числа записаны подряд, без разделения, причем второе число пред­ставлено как 0.

Теперь вставим по три пробела между числами.

FT = fopen(’Text2.txt’. ’w’);

Fprintf(FT.'%f ’.V);

fclose(FT);

В результате получим файл Text2.txt в таком виде, как показано на рис. 3.5.

Рис.3.5.Компоненты вектора разделены пробелами

Тот же вектор запишем в файл Text3.txt, пользуясь спецификатором %g.

FT = fopen( 'Text3.txt'. V);

Fprintf(FT.’ %g ’.V);

fclose(FT);

На рис. 3.6 показан результат. В отличие от предыдущих записей в формате с фик­сированной точкой, в данном случае второй элемент вектора отображен верно. Поэтому применение спецификатора %g при записи чисел в текстовый файл все­гда является предпочтительным.

Рис.3.6.Компоненты числового вектора в формате с плавающей точкой

Перейдем к записи в текстовый файл числовой матрицы. Сформируем матрицу:

» А = [1 -1.04е-28 7.8е45; -8.1234е-6 6.089 pi; 6 -1098 35]

А =

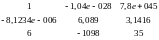
Запишем ее в текстовый файл Text4.txt:

FT = fopen('Text4.txt'. 'w');

fprintf(FT.'%g '.A);

fclose(FT);

Элементы матрицы в этом случае записываются в одну строку последовательно по столбцам (рис. 3.7).

Рис.3.7. Представление числовой матрицы в формате с плавающей точкой

Чтение данных из текстового файла может быть осуществлено с помощью одной из трех функций: fgetl, fgets или fscanf. При обращении к функции fgetl вида

str = fgetl(fid)

создается строка, состоящая из символов текстового файла данных с идентифи­катором fid, при этом символ конца строки удаляется. Если обратиться к функ­ции fgets следующим образом:

str = fgets(fid).

то в результате будет сформирована строка, состоящая из символов текстового файла данных с идентификатором fid, при этом символ конца строки сохраняет­ся. Функцию fscanf вызовем в таком виде:

str = fscanf(fid.format.size)

Она осуществляет считывание из файла того количества данных, которое указа­но в параметре size, преобразует данные из символьного в иной формат (напри­мер, числовой) в соответствии с параметром format и присваивает полученные значения элементам матрицы А. Параметр size, задаваемый в виде [m.n], где m и n — целые положительные числа, определяет соответственно количество строк и столбцов формируемой матрицы А. Параметр format должен быть строкой сим­волов (а значит, должен быть помещен между апострофами). В число этих симво­лов могут входить обычные символы, спецификаторы и управляющие последова­тельности символов, аналогичные упомянутым при описании функции fprintf. Отличие заключается лишь в том, что теперь эти спецификаторы указывают ко­личество символов, считываемых из файла, формат, в котором они считываются, и тип данных, в который преобразуются считанные символы (тип элементов мат­рицы А).

Наиболее удобной для считывания числовых данных является функция fscanf — единственная из функций считывания, формирующая числовые данные непосред­ственно в формате MATLAB.

Рассмотрим на примерах, как осуществляется воспроизведение записанных в файл данных при разных способах чтения. Прежде всего произведем чтение файла Textl.txt с использованием функции fscanf. Напомним, что запись в этот файл производилась без разделителей между числами. Такой же формат применим и для чтения данных.

» FT = fopen('Textl.txt'.’r’);

» Vnov = fscanf(FT. '%f .[1.4]);

» fclose(FT)

» Vnov

Vnov = 3.1416 0 -0.31257 0

В результате получаем вектор, в котором неверно отображено не только второе число (чего следовало ожидать, так как оно не записалось в текстовый файл (см. рис. 3.4), но и четвертое, которое было правильно записано в файл.

Картина меняется, если при записи между отдельными числами ставится какой- либо разделительный символ. Например, при записи вектора в файл Text2.txt та­ким символом был пробел. Прочитаем вектор из этого файла, используя тот же разделитель.

» FT = fopen('Text2.txt'. 'r');

» Vlnov = fscanf(FT. '%f ',[1.4]);

» fclose(FT);

» Vlnov

Vlnov = 3.1416 0 -0.31257 50890

Теперь четвертый элемент также считан верно.

Запись в файл Text3.txt была осуществлена в формате д, и все числа в нем отраже­ны без искажений. Считаем данные из этого файла в том же формате с тем же разделителем между числами.

» FT = fopen('Text3.txt','r');

» V2nov = fscanf(FT,’%g '.[1,4]);

» fclose(FT);

» V2nov

V2nov = 3.1416 1.457e-017 -0.31257 50890

Получается результат, в котором все числа отображены верно.

Считаем матрицу А из файла Text4.txt в том же формате, в котором она была запи­сана в этот файл.

» FT = fopen('Text4.txt'. 'r');

» Anov = fscanf(FT, '%g ’.[3.3]);

» fclose(FT);

» Anov

Anov =

В результате получаем матрицу В, которая полностью совпадает с исходной мат­рицей А.

Следует отметить, что при записи и чтении числовых массивов в текстовых фай­лах целесообразно использовать спецификатор %g и функцию fscanf. Это позволит избежать возможных искажений чисел. Необходимо также отделять одно число от другого каким-либо разделительным символом. При чтении числовых массивов нужно применять те же разделительные символы, что были применены в функции fprintf при их записи в файл

.Вопросы для самопроверки

1. Какие команды операционной среды можно выполнить в командном окне MATLAB?

2. Что представляет собой М-книга?

3. Как, находясь в текстовом редакторе Word, можно осуществлять расчеты и строить графики, используя MATLAB?

4. Какие типы файлов данных вы можете назвать и чем они отличаются друг от друга?

5. Какие средства используются в MATLAB для записи информации в бинарные файлы данных и чтения информации из них?

6. Какие средства предусмотрены в MATLAB для записи информации в тексто­вые файлы данных и чтения информации из них?

Каковы преимущества и недостатки использования бинарных и текстовых файлов данных для хранения и считывания информации?