
- •6. ##1.4.19.1(4) Найти обратную матрицу для данной .
- •9. ##2.8.25.1(2) При каких значениях и прямые и параллельны
- •10. ##1.5.32.2(1) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.52.2(1) Уравнение определяет
- •2. ##1.2.14.1(5) Дано: . Найти определитель матрицы а.
- •5. ##2.5.22.1(3) Расстояние от точки до плоскости вычисляется по формуле
- •6. ##1.4.13.1(1) Найти обратную матрицу для данной .
- •10. ##1.5.33.2(4) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.56.2(4) Уравнение определяет
- •6. ##1.4.14.1(2) Найти обратную матрицу для данной .
- •10. ##1.5.34.2(2) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.55.2(5) Уравнение определяет
- •2. ##1.2.14.1(5) Дано: . Найти определитель матрицы а.
- •5. ##2.5.22.1(3) Расстояние от точки до плоскости вычисляется по формуле
- •6. ##1.4.18.1(4) Найти обратную матрицу для данной .
- •10. ##1.5.35.2(1) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
- •12. ##2.4.48.2(4) Уравнение определяет
Вариант №5
1. ##1.1.25.1(1) Выбрать верные равенства, если А и В – квадратные матрицы порядка n:
Ответы:
1 ). все
предложенные ответы неверны
2 ).  3 ).
3 ).  4 ).
4 ).  5 ).
5 ). 
2.
##1.2.14.1(5) Дано:
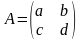 .
Найти определитель матрицы А.
.
Найти определитель матрицы А.
Ответы:
1 ).  2 ).
2 ). 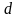 3 ).
3 ). 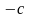 4 ).
4 ). 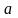 5 ).
5 ). 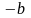
3. ##1.6.1.1(3) Два ненулевых вектора называются коллинеарными, если они
Ответы: 1 ). противоположно направлены 2 ). лежат в одной плоскости или на параллельных плоскостях 3 ). сонаправлены 4 ). имеют равную длину 5 ). лежат на одной или на параллельных прямых
4.
##2.1.20.1(4) Прямая на
плоскости задана уравнением
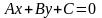 .
Какое из следующих утверждений верно?
1)
.
Какое из следующих утверждений верно?
1)
 - нормальный вектор прямой; 2)
- нормальный вектор прямой; 2)
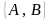 - направляющий вектор прямой; 3)
- направляющий вектор прямой; 4)
- нормальный вектор прямой; 5)
- точка, лежащая на прямой.
- направляющий вектор прямой; 3)
- направляющий вектор прямой; 4)
- нормальный вектор прямой; 5)
- точка, лежащая на прямой.
Ответы: 1 ). 5 2 ). 1 3 ). 4 4 ). 2 5 ). 3
5.
##2.5.22.1(3) Расстояние
от точки
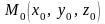 до плоскости
до плоскости
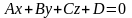 вычисляется по формуле
вычисляется по формуле
Ответы:
1 ). 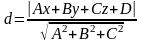 2 ).
2 ). 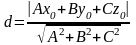 3 ).
3 ).  4 ).
4 ). 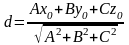 5 ).
5 ). 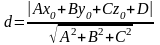
6.
##1.4.15.1(4) Найти обратную
матрицу для данной
 .
.
Ответы:
1 ). 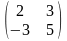 2 ). нет правильного ответа
3 ).
2 ). нет правильного ответа
3 ). 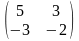 4 ).
4 ). 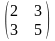 5 ).
5 ). 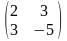
7.
##2.2.16.1(1) Написать
уравнение прямой, проходящей через
точку
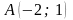 перпендикулярно вектору
перпендикулярно вектору
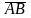 ,
если
,
если
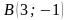
Ответы:
1 ).  2 ).
2 ).  3 ).
3 ). 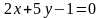 4 ).
4 ). 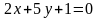 5 ).
5 ). 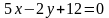
8.
##2.6.11.1(4) Написать
уравнение плоскости, проходящей через
точку
 с нормальным вектором
с нормальным вектором
 .
.
Ответы:
1 ). 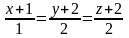 2 ).
2 ).  3 ).
3 ).  4 ).
4 ).  5 ).
5 ). 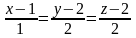
9.
##2.8.23.1(2) При каких
значениях
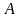 и
и
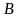 прямые
прямые
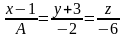 и
и
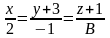 параллельны
параллельны
Ответы:
1 ). 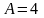 ;
;
 2 ).
2 ).  ;
;
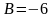 3 ).
3 ). 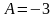 ;
;
 4 ).
4 ).  ;
;
 5 ).
5 ).  ;
;
10.
##1.5.31.2(1) Определить,
имеет ли система решение, если да, то
решить систему уравнений
по формулам Крамера

Ответы:
1 ). 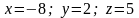 2 ).
2 ).  3 ).
3 ). 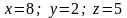 4 ). бесчисленное множество
решений 5 ). система
уравнений несовместна
4 ). бесчисленное множество
решений 5 ). система
уравнений несовместна
11.
##1.8.54.2(2) Сила
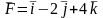 приложена к точке M(1,2,3).
Найти момент этой силы относительно
точки А(3,2,-1).
приложена к точке M(1,2,3).
Найти момент этой силы относительно
точки А(3,2,-1).
Ответы:
1 ). 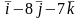 2 ).
2 ).  3 ).
3 ).  4 ).
4 ). 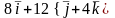 5 ). нет правильного ответа
5 ). нет правильного ответа
12.
##2.4.59.2(4) Уравнение
 определяет
определяет
Ответы: 1 ). эллипс 2 ). гиперболу 3 ). точку 4 ). две пересекающиеся прямые 5 ). окружность
13.
##2.10.27.2(4) Составить
уравнение плоскости, проходящей через
две параллельные прямые
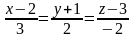 и
и
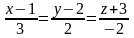
Ответы:
1 ). 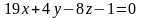 2 ).
2 ). 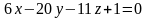 3 ).
3 ).  4 ).
4 ). 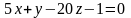 5 ).
5 ). 
14.
##2.4.169.3(2) Кривая,
определяемая уравнением
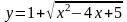 ,
изображена на рисунке
,
изображена на рисунке
Ответы:
1 ). 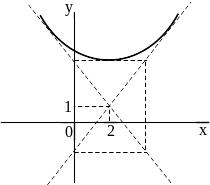 2 ).
2 ). 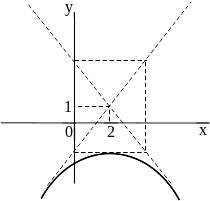 3 ).
3 ).  4 ).
4 ).  5 ).
5 ). 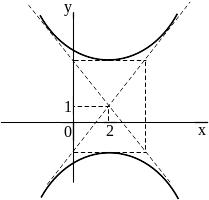
15.
##2.12.29.3(3) Поверхность,
определяемая уравнением
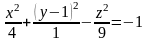 изображена на рисунке
изображена на рисунке
Ответы:
1 ). 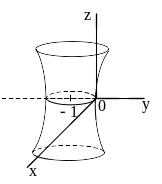 2 ).
2 ). 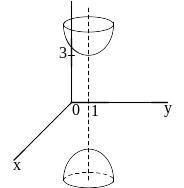 3 ).
3 ). 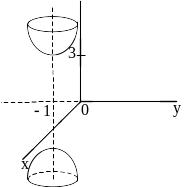 4 ).
4 ). 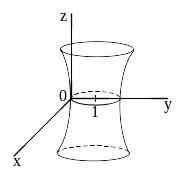 5 ).
5 ). 
Вариант №4
1. ##1.1.27.1(5) Из приведенных ответов выбрать матрицу.
Ответы:
1 ).  2 ).
2 ). 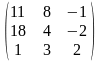 3 ).
3 ). 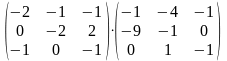 4 ).
4 ). 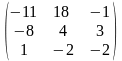 5 ).
5 ). 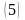
2.
##1.2.1.1(1) Закончить
утверждение. Определитель матрицы
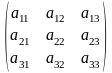 равен…
равен…
Ответы:
1 ). нет
правильного ответа
2 ).  3 ).
3 ). 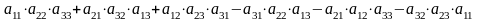 4 ).
4 ). 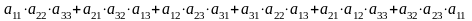 5 ).
5 ). 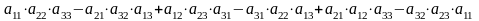
3. ##1.6.2.1(1) Векторы называются компланарными, если они
Ответы: 1 ). сонаправлены 2 ). противоположно направлены 3 ). имеют одно начало 4 ). лежат в одной плоскости или на параллельных плоскостях 5 ). лежат на одной или на параллельных прямых
4. ##2.1.7.1(1) Уравнение прямой с угловым коэффициентом имеет вид
Ответы:
1 ). 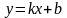 2 ).
2 ).  3 ).
3 ). 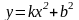 4 ).
4 ).  5 ).
5 ).
5. ##2.5.1.1(1)
З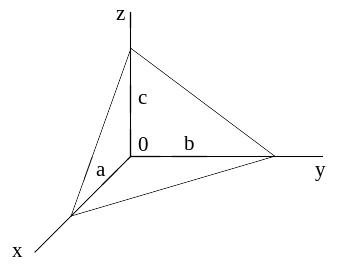 адание:
Уравнение плоскости, изображенной на
рисунке, имеет вид
адание:
Уравнение плоскости, изображенной на
рисунке, имеет вид
Ответы:
1 ). 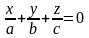 2 ).
2 ). 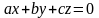 3 ).
3 ).  4 ).
4 ).  5 ).
5 ). 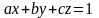
6. ##1.4.19.1(4) Найти обратную матрицу для данной .
Ответы:
1 ). 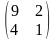 2 ). нет правильного ответа
3 ).
2 ). нет правильного ответа
3 ). 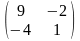 4 ).
4 ). 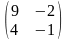 5 ).
5 ). 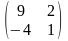
7.
##2.2.22.1(1) Найти
расстояние от начала координат до прямой
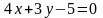
Ответы:
1 ). 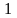 2 ).
2 ). 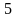 3 ).
3 ). 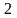 4 ).
4 ).  5 ).
5 ). 
8.
##2.6.10.1(4) Написать
уравнение плоскости, проходящей через
точку
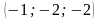 перпендикулярно вектору
перпендикулярно вектору
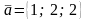 .
.
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
9. ##2.8.25.1(2) При каких значениях и прямые и параллельны
Ответы: 1 ). ; 2 ). ; 3 ). ; 4 ). ; 5 ). ;
10. ##1.5.32.2(1) Определить, имеет ли система решение, если да, то решить систему уравнений по формулам Крамера
Ответы:
1 ).  2 ).
2 ).  3 ). система уравнений несовместна
4 ).
3 ). система уравнений несовместна
4 ). 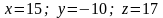 5 ). бесчисленное множество
решений
5 ). бесчисленное множество
решений
11.
##1.8.55.2(1) Сила
 приложена к точке Е(4,5,9). Найти момент
этой силы относительно точки К(9,5,-1).
приложена к точке Е(4,5,9). Найти момент
этой силы относительно точки К(9,5,-1).
Ответы:
1 ). нет
правильного ответа
2 ).  3 ).
3 ). 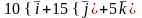 4 ).
4 ). 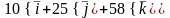 5 ).
5 ). 
12. ##2.4.52.2(1) Уравнение определяет
Ответы: 1 ). параболу 2 ). гиперболу 3 ). эллипс 4 ). две пересекающиеся прямые 5 ). окружность
13.
##2.10.25.2(5) составить
уравнение плоскости, проходящей через
точку
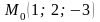 параллельно прямым
параллельно прямым
 ,
,
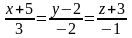
Ответы:
1 ).  2 ).
2 ). 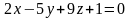 3 ).
3 ). 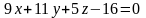 4 ).
4 ). 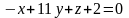 5 ).
5 ). 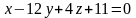
14.
##2.4.170.3(3) Кривая,
определяемая уравнением
 ,
изображена на рисунке
,
изображена на рисунке
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
15.
##2.12.30.3(2) Поверхность,
определяемая уравнением
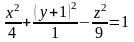 изображена на рисунке
изображена на рисунке
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
Вариант №3
1. ##1.1.28.1(3) Выбрать матрицу размерности (32)
Ответы:
1 ). 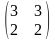 2 ).
2 ). 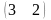 3 ).
3 ).  4 ). все предложенные ответы
неверны 5 ).
4 ). все предложенные ответы
неверны 5 ). 
2. ##1.2.14.1(5) Дано: . Найти определитель матрицы а.
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
3.
##1.6.4.1(4) Закончить
утверждение. Вектор называется
противоположным вектору
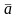 ,
если он…
,
если он…
Ответы:
1 ). сонаправлен
с
2 ). противоположно направлен
по отношению к
3 ). противоположно направлен с
и имеет с ним одинаковую длину
4 ). имеет одинаковую длину с
5 ). имеет длину -
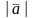
4. ##2.1.8.1(2) Уравнение прямой в отрезках имеет вид
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
5. ##2.5.22.1(3) Расстояние от точки до плоскости вычисляется по формуле
Ответы: 1 ). 2 ). 3 ). 4 ). 5 ).
6. ##1.4.13.1(1) Найти обратную матрицу для данной .
Ответы:
1 ). 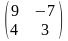 2 ).
2 ). 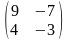 3 ).
3 ). 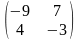 4 ). нет правильного ответа
5 ).
4 ). нет правильного ответа
5 ). 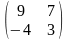
7.
##2.2.27.1(5) Даны вершины
треугольника
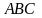 :
:
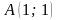 ,
,
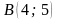 ,
,
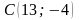 .
Написать уравнение прямой, проходящей
через вершину
параллельно стороне
.
Написать уравнение прямой, проходящей
через вершину
параллельно стороне

Ответы:
1 ). 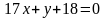 2 ).
2 ).  3 ).
3 ).  4 ).
4 ). 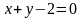 5 ).
5 ). 
8.
##2.6.12.1(5) Написать
уравнение плоскости, отсекающей на осях
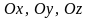 соответственно отрезки 2; -1; 4.
соответственно отрезки 2; -1; 4.
Ответы:
1 ). 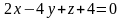 2 ).
2 ). 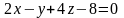 3 ).
3 ). 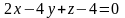 4 ).
4 ).  5 ).
5 ). 
9.
##2.8.26.1(1) При каком
значении
прямые
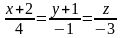 и
и
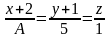 перпендикулярны
перпендикулярны
Ответы:
1 ).
2 ).
3 ).
4 ). 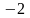 5 ).
5 ).
