3.5. Закон сохранения механической энергии. Закон сохранения и превращения энергии как проявление неуничтожимости материи и ее движения

Рассмотрим систему, состоящую из nчастиц с массамиm₁,m₂,…m_n.Пусть частицы взаимодействуют друг с другом с силамиF_ik, модули которых зависят только от расстояния между частицами. Такие силы являются консервативными. Это означает, что работа, совершаемая этими силами над частицами, определяется начальной и конечной конфигурациями системы. Предположим, что кроме внутренних сил наi–частицу действует внешняя консервативная силаf_iи внешняя неконсервативная сила. Тогда уравнение движенияi–частицы будет иметь вид

, (3.25)

причем (ik), и принимает значенияi=1,2…n.

Умножив уравнение (3.25) на 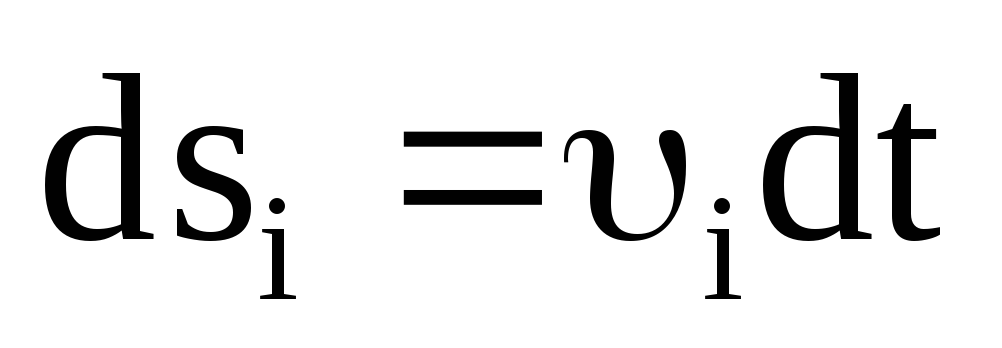и, сложив вместе всеnуравнений, получим

. (3.26)

Левая часть уравнения (3.26) есть приращение кинетической энергии системы:

.

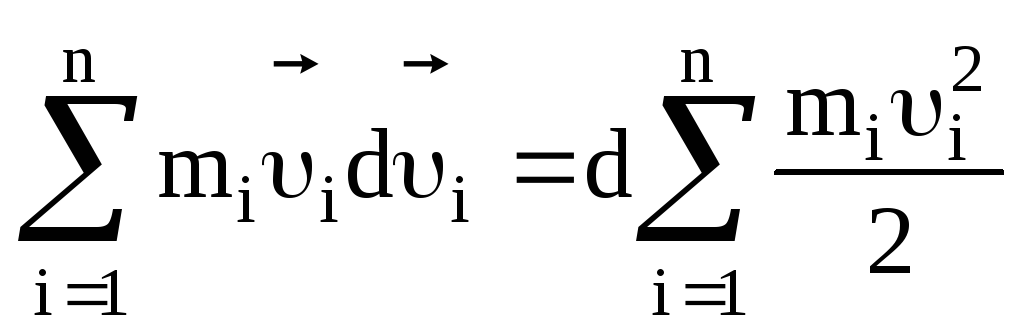Первый член правой части равен убыли потенциальной энергии взаимодействия частиц. Второй членравен убыли потенциальной энергии системы во внешнем поле консервативных сил. Последний членпредставляет собой работунеконсер-вативных внешних сил.

Таким образом, равенство (3.26) можно записать в виде

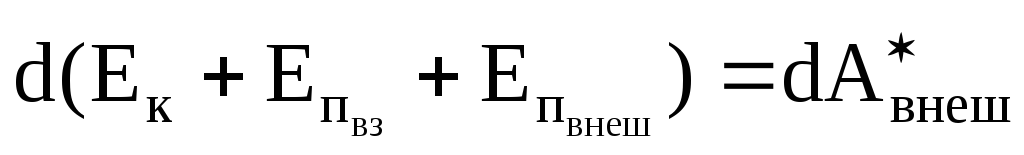. (3.27)

Величина - есть полная механическая энергия системы. Если внешние неконсервативные силы отсутствуют, правая часть уравнения (3.27) будет равна нулю, и полная энергия системы остается постоянной:

.

41