6.4. Затухающие колебания

Всякое реальное колебание происходит с постепенным расходованием энергии движения на работу против сил трения. При этом амплитуда и скорость колебательного движения убывают. Полная сила, действующая на колеблющуюся точку, будет тогда суммой квазиупругой силы и силы трения:

F = F_упр+F_тр

При малых скоростях движения сопротивление обычно пропорционально первой степени скорости и направлено противоположно ей:

F_тр= r,

где r - коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.

Уравнение движения тела в этом случае имеет вид

F_упр+F_тр;

. (6.27)

Введем обозначения

;

и перепишем уравнение (6.27):

, (6.28)

где ₀ - собственная частота колебания системы.

Будем искать решение уравнения (6.28) в виде

, (6.29)

где A(t) - некоторая функция времени.

Найдем первую производную от уравнения (6.29):

(6.30)

и вторую производную:

. (6.31)

Подставляя уравнения (6.29), (6.30), (6.31) в (6.28), получим

Сгруппируем члены при cos(t+) и sin(t+):

.

Для того, чтобы данное уравнение удовлетворялось при любых значениях t, необходимо равенство нулю коэффициентов при cos(t+) и sin(t+).

Таким образом, мы приходим к двум уравнениям:

; (6.32)

. (6.33)

Из уравнения (6.32) получим .

Проинтегрируем выражение

;

.

Производя потенцирование найденного соотношения, получим выражение для амплитуды колебаний:

A=A₀e^-t.

Легко увидеть, что , а.

Подстановка этих значений в уравнение (6.33) приводит к соотношению

,

из которого после сокращения А получаем

, .

При частота затухающих колебаний будет величиной вещественной, и решением дифференциального уравнения (6.28) является функция вида

. (6.34)

График этой функции дан на рис.6.15.

Сравнивая полученное решение (6.34) решением уравнений гармонических колебаний

x=Acos(t+),

следует заметить, что последние отличаются от чисто гармонических колебаний тел, что амплитуда колебания

является убывающей функцией времени.

На графике (рис.6.15) она показана пунктирной линией. Величина называ-ется показателем затухания,- частотой коле-бания. Период колебания определяется из соотношений

x A0 O t -A0 Рис.6.15

;

или .

С увеличением трения период колебаний возрастает, а при =₀ период становится бесконечным. При дальнейшем увеличении  период становится мнимым, а движение точки или тела – апериодическим (рис.6.16). Вычислим отношение амплитуд, отстоящих друг от друга во времени на один период:

.

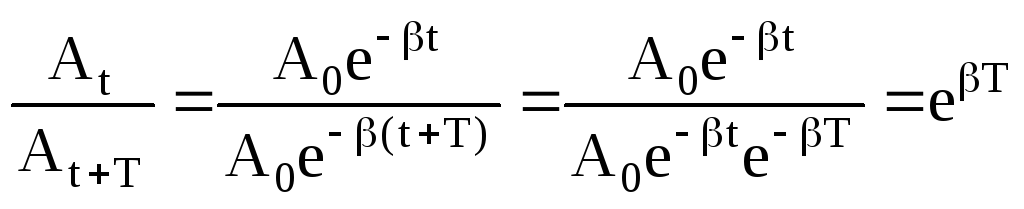x O t Рис.6.16

Отношение амплитуд зату-хающих колебаний, отстоящих друг от друга на интервал времени, равный периоду, постоянно во все время колебания. Натуральный лога-рифм этого отношения называется логарифмическим декрементом затухания: ; .

Логарифмический декремент затухания характеризующий быстроту убывания амплитуды, прямо пропорционален величине коэффициента сопротивления и обратно пропорционален массе системы. Таким образом, из-за наличия сил трения собственные колебания точки или тела будут затухающими.