
- •6.6. Волновые процессы
- •6.6.1. Плоская синусоидальная волна. Фазовая скорость. Длина волны. Групповая скорость
- •6.6.2. Скорость распространения волн в упругой среде
- •6.6.3. Поток энергии в волновых процессах
- •6.6.4. Принцип Гюйгенса-Френеля. Интерференция волн
- •6.6.5. Отражение волн. Стоячие волны
- •7. Молекулярно-кинетическая теория
- •7.1. Статистический метод исследования. Термодинамический метод исследования. Термодинамические параметры. Равновесное состояние и процессы их изображения на термодинамических диаграммах
- •7.2. Основное уравнение молекулярно-кинетической теории газов
- •7.3. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Связь основного уравнения мкт с уравнением Менделеева-Клайперона
7.2. Основное уравнение молекулярно-кинетической теории газов
При ударе о стенку сосуда молекула сообщает ей импульс, численно равный изменению количества движения молекулы. Каждый элемент поверхности стенки s непрерывно подвергается бомбардировке большим количеством молекул, в результате чего за время t получает суммарный импульс, направленный по нормали к s. Отношение импульса к t, как известно, есть сила, действующая на s и есть давление. Для получения этого давления введем два упрощения, касающиеся характера движения молекул.
|
Будем полагать,
что моле-кулы движутся только вдоль
трех взаимно перпендикулярных
на-правлений. Если газ содержит N
молекул, то в любой момент времени
вдоль каждого из направлений будет
двигаться
|
Рис.7.1 |
них,
т.е.
![]() ,
движется вдоль данного направления в
одну сторону, половина – в противоположную
сторону (рис.7.1). Основываясь на таком
предположении, мы будем считать, что в
интересующем нас направлении движется
,
движется вдоль данного направления в
одну сторону, половина – в противоположную
сторону (рис.7.1). Основываясь на таком
предположении, мы будем считать, что в
интересующем нас направлении движется![]() часть молекул.
часть молекул.
Второе упрощение состоит в том, что всем молекулам мы придадим одинаковое значение скорости. Вычислим импульс, сообщаемый стенке сосуда, ударяющейся об него молекулой. До удара о стенку количество движения молекулы направлено по внешней нормали к s и равно m (рис.7.2). В результате удара количество движения меняет знак.
Таким образом, приращение количества движения молекулы равно
(m) ( m) = 2m.
По третьему закону Ньютона стенка получит при ударе импульс 2m, имеющий направление нормали.
|
m
s
Рис.7.2
|
Согласно второму закону Ньютона, для N молекул полу-чим равенство Ft = 2mN, где Ft - импульс силы, 2mN - удвоенный импульс N моле-кул. За время t до элемента стен- |
ки s долетят все движущиеся по направлению к нему молекулы, заключенные в объеме цилиндра с основанием s и высотой t. Число этих молекул равно
![]() ,
,
где n - число молекул в единице объема.
Число ударов молекул о площадку s за единицу времени будет равно
![]() .
.
Умножим число ударов на импульс, сообщаемый стенке при каждом ударе, получим суммарный импульс, сообщаемый элементу стенки за время t,
![]() ,
,
т.е.
![]() .
.
Разделив эту величину на s и t, получим давление газа, оказываемое на стенки сосуда
![]() .
(7.1)
.
(7.1)
Учитывая, что
![]() - кинетическая энергия поступательного
движения молекулы, предыдущее выражение
можно записать в виде
- кинетическая энергия поступательного
движения молекулы, предыдущее выражение
можно записать в виде
![]() .
(7.2)
.
(7.2)
Если в выводе учесть, что скорости отдельных молекул i будут различны, то величину n2 следует заменить суммой квадратов ско-
ростей каждой из молекул, находящихся в единице объема
![]() .
.
Отсюда видно, что
в (7.1) следует заменить 2
на
![]() ,
так как
,
так как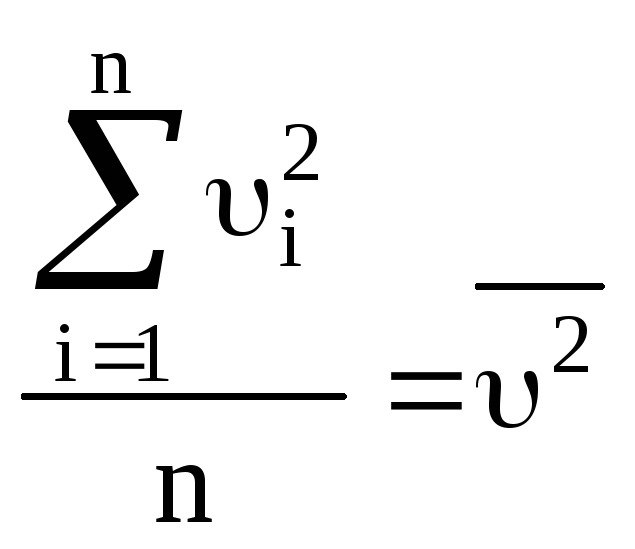 - средний квадрат скорости, и переписать
уравнение (7.2) в виде
- средний квадрат скорости, и переписать
уравнение (7.2) в виде
![]() ,
,
где средняя кинетическая энергия поступательного движения молекулы
![]() .
.
Соотношение
![]() .
(7.3)
.
(7.3)
называется основным уравнением молекулярно-кинетической теории (МКТ) идеального газа.

 -m
-m