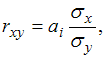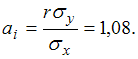6. Статистические методы моделирования связи социально-экономических явлений и процессов

Вычислено уравнение регрессии между себестоимостью единицы продукции и накладными расходами:  . Это означает, что по мере роста накладных расходов на 1 рубль себестоимость единицы продукции повышается на …

Решение:

Коэффициент парной линейной регрессии имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Он измеряет среднее по совокупности отклонение у от его средней величины при отклонении признака х от своей средней величины на принятую единицу измерения.

Так, при росте накладных расходов на 1 рубль себестоимость единицы продукции повышается на 5 копеек.

Теория статистики :  учеб. / Р. А. Шмойлова,[ и др. ]; под ред. Р. А. Шмойловой. – 5-е изд. –М.: Финансы и статистика, 2007. - С. 353 - 357.

Межгрупповая дисперсия равна 30, общая дисперсия равна 180. Коэффициент детерминации равен …

Решение:

Коэффициент детерминации определяют как долю межгрупповой дисперсии в общей дисперсии признака-результата. Он показывает влияние изучаемого фактора на часть общей вариации признака-результата:

Статистика : учеб. / под ред. И. И. Елисеевой. – М. : Высшее образование, 2007.  –  С. 77 - 78.

Оценка значимости параметров модели регрессии осуществляется на основе …

Решение:

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза (Н₀) о равенстве коэффициента корреляции нулю. Если расчетное значение больше табличного, гипотеза Н₀ отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно и о статистической существенности зависимости между признаками.

Данный критерий оценки значимости применяется для совокупностей n < 50.

Теория статистики :  учеб. / Р. А. Шмойлова,[ и др. ]; под ред. Р. А. Шмойловой. – 5-е изд. –М.: Финансы и статистика, 2007. - С.353 - 357.

По следующим данным:   – составьте линейное уравнение регрессии.

Решение:

Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выраженная формулой

где a_i – коэффициент регрессии в уравнении связи;

σ_х , σ_у – среднее квадратическое отклонение признаков.

Выразим а_i 

Линейное уравнение регрессии:

Теория статистики :  учеб. / Р. А. Шмойлова,[ и др. ]; под ред. Р. А. Шмойловой. – 5-е изд. –М.: Финансы и статистика, 2007. - С.361 - 363.

Связь между признаками можно признать существенной при значении линейного коэффициента корреляции …

Решение:

По степени тесноты связи различают количественные критерии оценки тесноты связи:

Сзязь считается существенной при значении коэффициента корреляции, находящемся в пределах ±0,7 – ±1,0.

Теория статистики :  учеб. / Р. А. Шмойлова,[ и др. ]; под ред. Р. А. Шмойловой. – 5-е изд. –М. : Финансы и статистика, 2007. - С. 365.