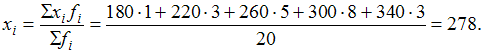5. Метод средних величин и вариационный анализ

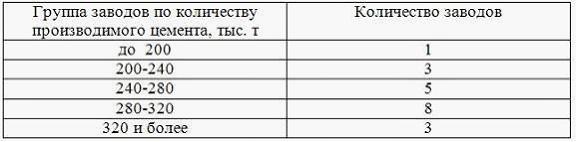
Имеется следующее распределение 20 заводов по производству цемента за год:

Среднее производство цемента на один завод составляет …

Решение:

Дан ряд распределения заводов по количеству производства цемента. Одни и те же значения признака повторяются, поэтому средняя определяется по средней арифметической взвешенной. Для этого нужно перемножить (взвесить) варианты признака на число единиц, соответствующих каждому варианту, то есть на их частоты:

Ряд распределения является интервальным, потому нужно определить середину каждого интервала признака. Она вычисляется как полусумма нижних и верхних границ интервалов. Середина открытых интервалов, первого и последнего, определяется по величине интервалов соответственно последующего и предыдущего.

Статистика : учеб. / под ред. И. И. Елисеевой. – М.: Высшее образование, 2007.  –  С.51-54.

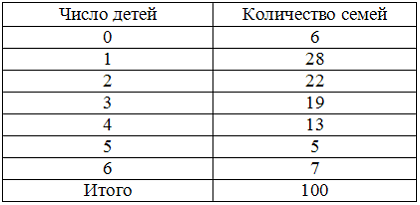
Имеются данные о распределении 100 семей по количеству детей в семье:

Мода равна …

Решение:

Мода в дискретном ряду распределения представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Самая большая частота 28, и ей соответствует значение признака – 1 ребенок в семье.

Статистика : учеб. / под ред. И. И. Елисеевой. – М.: Высшее образование, 2007.  –  С.59.

Если каждое значение признака увеличить на 10 единиц, то средняя …

Решение:

Средняя арифметическая обладает рядом свойств, которые могут быть использованы для упрощения ее вычисления. В данном случае применяется следующее свойство средней: если от каждого значения признака отнять или к каждому его значению прибавить одно какое-либо число А, то новая средняя соответственно уменьшится или увеличится на то же самое число.

Статистика : учеб. / под ред. И. И. Елисеевой. – М.: Высшее образование, 2007.  –  С.55.

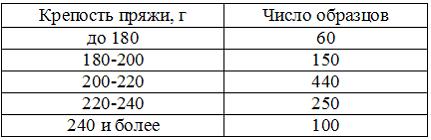
Имеются следующие данные о лабораторных испытаниях 1000 образцов пряжи на крепость

Средняя крепость пряжи составляет …

Решение:

Ряд распределения содержит варианты признака и частоты. Поэтому средняя крепость пряжи вычисляется по средней арифметической взвешенной. Для этого нужно перемножить (взвесить) варианты признака на число единиц, соответствующих каждому варианту, то есть на их частоты:

Ряд распределения является интервальным, потому нужно определить середину каждого интервала признака. Она вычисляется как полусумма нижних и верхних границ интервалов. Середина открытых интервалов, первого и последнего, определяется по величине интервалов соответственно последующего и предыдущего.

Статистика : учеб. / под ред. И. И. Елисеевой. – М.: Высшее образование, 2007.  –  С.51-54.

По данным о среднем балле успеваемости и количестве студентов в каждой из академических групп факультета средний балл успеваемости студентов по факультету в целом определяется по средней …

Решение:

Средний балл успеваемости по группам является признаком, а количество студентов по каждой академической группе – частотой, поэтому средний балл успеваемости по факультету рассчитывается по средней арифметической взвешенной.

Статистика : учеб. / под ред. И. И. Елисеевой. – М.: Высшее образование, 2007.  –  С.51-54.