11. Закон полного тока (циркуляция вектора магнитной индукции) для магнитного поля в вакууме и его применение к расчету магнитного поля бесконечно длинного соленоида.

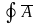d - циркуляция

d = - Закон полного тока.

d =MM₀ - Закон полного тока.

Ц иркуляция вектора напряженности магнитного поля вдоль прямоугольного контура равно алгебраической сумме токов охватываемых кольцевым контуром.

Применение закона полного тока:

Первое: учитывать каждый ток столько раз, сколько он охватывается контуром.

Второе: если направление тока связано с направлением обхода контура правилом правого винта, то ток считать положительным, в противном случае отрицательным.

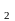d =-I +I -I =-I

Применение закона полного тока для расчета колебаний.

А) прямолинейный бесконечно длинный проводник

В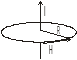 ыберем контур в виде окружности с радиусом r.

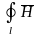d =H2L==I

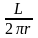H= ;B=

В) Поле соленоида. Соленоид представляет собой цилиндрическую катушку с большим количеством витков, намотанных вплотную на общий сердечник.

d =Hl=IN

H=I =I*n – поле внутри соленоид, где n- число витков на единицу длины.

12. Контур с током в магнитном поле.

Всякий электрический ток создает магнитное поле. Интенсивность магнитного поля в данной точке характеризуется вектором магнитной индукции . Величина и направление этого вектора определяется законом Био-Савара-Лапласа.

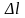= I sin .

Здесь - магнитная индукция в точке А, создаваемая током I,протекающим через элемент провода

длиной , = 4*10^-7Ом*с.

13. Магнитный поток, теорема Остроградского–Гаусса.

Поскольку значение В численно равно количеству линий индукции, проходящих через единицу площади , перпендикулярной к ним, то Ф=В есть общее число линий ндукции магнитного поля, пронизывающих площадь ,если индукция В во всех точках поверхности одинакова. Величину Ф принято называть магнитным потоком или, потоком вектор В через поверхность . Магн.поток – скалярная величина. Единица магн.потока – 1Вб.

Теорема Гаусса: Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

теорема Остроградского-Гаусса:

14. Работа перемещения проводника с током в магнитном поле.

Так как на проводник с током в магн.поле действуют силы, т при перемещении этого проводника будет совершаться работа. На проводник l будет действовать сила Ампера F_A, и он начнет перемещаться вправо. Подсчитаем работу при перемещении проводника l на расстояние b. Если направления силы и перемещения совпадают и т.к. F_A=B I l, то имеем

А=F_Ab=B I l b;

Если площадь при начальном положении проводника l обозначить через S₁, а при конечном положении через S₂, то ΔS=S₂-S₁=lb, есть изменение площади, охваченной током при перемещении проводника l. Тогда A=BIΔS. Обозначив произведение BS через Ф, получим

BΔS=B(S₂-S₁)=BS₂-BS₁=Ф₂-Ф₁=ΔФ. Итак работа при перемещении проводника с током в магн.поле выражается формулой A=IΔФ, где Ф=BS(перпендик.) [1Вб] – магнитный поток или поток вектора В через поверхность S(перепендикулярно)

15.Магнитное поле Земли.

Исследование поведения магнитных стрелок в различных точках земного шара привели к выводу о существовании магнитного поля Земли. Это поле в основном обусловлено процессами, протекающими в жидком металлическом ядре Земли. Магнитные полюсы Земли не совпадают с ее географическими полюсами: вблизи северного географического полюса Земли находится ее южный магнитный полюс, причем угол между осью вращения Земли и линией, соединяющей ее магнитные полюсы, составляет 11,5°.