Введение:

Термин постоянный ток не совсем корректен: в действительности для постоянного тока неизменным является прежде всего значение напряжения (измеряется в Вольтах), а не значение тока (измеряется в Амперах), хотя значение тока также может быть неизменным. Путаница возникла в результате того, что термин ток употребляется для описания электрических процессов вообще. Поэтому термин постоянный ток следует понимать как постоянное напряжение. Далее будем использовать термин именно в этом смысле.

Термин постоянный ток имеет несколько значений:

• Питающее напряжение, величина которого не зависит от времени. Пример: устройство запитано от источника постоянного тока. В данном смысле использование термина постоянный ток (так же, как и переменный ток) подчёркивает «силовой» характер данного сигнала, то есть это электрический сигнал, передающий мощность, предназначенный для питания электрических устройств. В других смыслах используют более точные термины: напряжение, сигнал и т.п.

• Постоянная составляющая сигнала.

• Термин также может использоваться не в смысле напряжения, а в смысле частоты сигнала (для постоянного тока она нулевая). Пример: рабочий диапазон частот: от постоянного тока до 1 МГц

Применение: Постоянный ток широко используется в технике: подавляющее большинство электронных схем в качестве питания используют постоянный ток. Переменный ток используется преимущественно для более удобной передачи от генератора до потребителя. Иногда в некоторых устройствах постоянный ток преобразуют в переменный ток преобразователями (инверторами).

1.УСЛОВИЯ  СУЩЕСТВОВАНИЯ   ЭЛЕКТРИЧЕСКОГО ТОКА

Для возникновения и поддержания тока в какой-либо среде необходимо выполнение двух условий:

	наличие в среде свободных электрических зарядов
	создание в среде электрического поля.

В разных средах носителями электрического тока являются разные заряженные частицы.

Электрическое поле в среде необходимо для создания направленного движения свободных зарядов. Как известно, на заряд q в электрическом поле напряженностью E действует сила F = q* E, которая и заставляет свободные заряды двигаться в направлении электрического поля. Признаком существования в проводнике электрического поля является наличие не равной нулю разности потенциалов между любыми двумя точками проводника,

Однако, электрические силы не могут длительное время поддерживать электрический ток. Направленное движение электрических зарядов через некоторое время приводит к выравниванию потенциалов на концах проводника и, следовательно, к исчезновению в нем электрического поля.

Для поддержания тока в электрической цепи на заряды кроме кулоновских сил должны действовать силы неэлектрической природы (сторонние силы).

Устройство, создающее сторонние силы, поддерживающее разность потенциалов в цепи и преобразующее различные виды энергии в электрическую энергию, называется источником тока.

Для существования электрического тока в замкнутой цепи необходимо включение в нее источника тока.

Основные характеристики:

1. Сила тока - I, единица измерения - 1 А (Ампер).

Силой тока называется величина, равная заряду, протекающему через поперечное сечение проводника за единицу времени.

I = q/t .   (1)

Формула (1) справедлива для постоянного тока, при котором сила тока и его направление не изменяются со временем. Если сила тока и его направление изменяются со временем, то такой ток называется переменным.

Для переменного тока:

I = lim q/t , (*) t - 0

т.е. I = q', где q' - производная от заряда по времени.

2. Плотность тока - j, единица измерения - 1 А/м².

Плотностью тока называется величина, равная силе тока, протека-ющего через единичное поперечное сечение проводника:

j = I/S .   (2)

3. Электродвижущая сила источника тока - э.д.с. (  ), единица измерения - 1 В (Вольт). Э.д.с.- физическая величина, равная работе, совершаемой сторонними силами при перемещении по электрической цепи единичного положительного заряда:

 = А_ст./q . (3)

4. Сопротивление проводника - R, единица измерения - 1 Ом.

Под действием электрического поля в вакууме свободные заряды двигались бы ускоренно. В веществе они движутся в среднем равномерно, т.к. часть энергии отдают частицам вещества при столкновениях.

Теория утверждает, что энергия упорядоченного движения зарядов рассеивается на искажениях кристаллической решетки. Исходя из природы электрического сопротивления, следует, что

R = *l/S ,  (4)

где

l - длина проводника, S - площадь поперечного сечения,  - коэффициент пропорциональности, названный удельным сопротивлением материала.

Эта формула хорошо подтверждается на опыте.

Взаимодействие частиц проводника с движущимися в токе зарядами зависит от хаотического движения частиц, т.е. от температуры проводника. Известно, что

 = ₀(1 + t) ,   (5)

R = R₀(1 +t) .  (6).

Коэффициент  называется температурным коэффициентом сопротив-ления:

 = (R - R₀)/R₀*t .

Для химически чистых металлов  > 0 и равно 1/273 К^-1. Для сплавов температурные коэффициенты имеют меньшее значение. Зависимость (t) для металлов линейная:

В 1911 году открыто явление сверхпроводимости, заключающееся в том, что при температуре, близкой к абсолютному нулю, сопротивление некоторых металлов падает скачком до нуля.

У некоторых веществ (например, у электролитов и полупроводников) удельное сопротивление с ростом температуры уменьшается, что объясняется ростом концентрации свободных зарядов.

Величина, обратная удельному сопротивлению, называется удельной электрической проводимостью 

  = 1/ . (7)

5. Напряжение - U , единица измерения - 1 В.

Напряжение - физическая величина, равная работе, совершаемой сторонними  и электрическими силами при перемещении единичного положительного заряда.

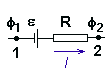
U = (A_ст.+ А_эл.)/q .   (8)

Так как  А_ст./q = , а  А_эл./q = __, то

U =  + (__

2. ЗАКОНЫ ПОСТОЯННОГО ТОКА:

Электрический ток. Сила тока. Закон Ома для участка цепи. Сопротивление проводников. Последовательное и параллельное соединение проводников. Электродвижущая сила. Закон Ома для полной цепи. Работа и мощность тока.

Всякое движение электрических зарядов называют электрическим током. В металлах могут свободно перемещаться электроны, в проводящих растворах - ионы, в газах могут существовать в подвижном состоянии и электроны, и ионы.

Условно за направление тока считают направление движения положительных частиц, поэтому в металлах это направление противоположно направлению движения электронов.

Плотность тока - величина заряда, проходящего в единицу времени через единицу поверхности, перпендикулярной к линиям тока. Эта величина обозначается j и рассчитывается следующим образом:

j=nev.

Здесь n - концентация заряженных частиц, e - заряд каждой из частиц, v - их скорость.

Сила тока i - величина заряда, проходящего в единицу времени через полное сечение проводника. Если за время dt через полное сечение проводника прошел заряд dq, то

i=(dq)/(dt).

По другому, сила тока находится интегрированием плотности тока по всей поверхности любого сечения проводника. Единица измерения силы тока - Ампер. Если состояние проводника (его температура и др.) стабильно, то между приложенным к его концам напряжением и возникающим при этом током существует однозначная связь. Она называется Закон Ома и записывается так:

I=U/R.

R - электрическое сопротивление проводника, зависящее от рода вещества и от его геометрических размеров. Единичным сопротивлением обладает проводник, в котором возникает ток 1 А при напряжении 1 В. Эта единица сопротивления называется Ом.

Закон Ома в дифференциальной форме:

j=E,

где j - плотность тока, Е - напряженность поля,  - проводимость. В этой записи закон Ома содержит величины, характеризующие состояние поля в одной и той же точке.

Различают последовательное и параллельное соединения проводников. При последовательном соединении ток, протекающий по всем участкам цепи, одинаков, а напряжение на концах цепи складывается как алгебраическая сумма напряжений на всех участках.

R=(Ri).

При параллельном соединении проводников постоянным остается напряжение, а ток складывается из суммы токов, протекающих по всем ветвям. В этом случае складываются величины, обратные сопротивлению:

1/R=(1/Ri).

Для получения постоянного тока на заряды в электрической цепи должны действовать силы, отличные от сил электростатического поля; их называют сторонними силами.

Если рассматривать полную электрическую цепь, необходимо включить в нее действие этих сторонних сил и внутренне сопротивление источника тока r. В этом случае закон Ома для полной цепи примет вид:

I=E/(R+r).

Е - электродвижущая сила (ЭДС) источника. Она измеряется в тех же единицах, что и напряжение. Величину (R+r) называют иногда полным сопротивлением цепи.

Сформулируем правила Киркгофа: Первое правило: алгебраическая сумма сил токов в участках цепи, сходящихся в одной точке разветвления, равна нулю.

Второе правило: для любого замкнутого контура сумма всех падений напряжения равна сумме всех ЭДС в этом контуре.

Мощность тока рассчитывается по формуле

P=UI=I²R=U²/R.

Закон Джоуля-Ленца. Работа электрического тока (тепловое действие тока) A=Q=UIt=I²Rt=U²t/R.

Электронная проводимость металлов. Сверхпроводимость. Электрический ток в растворах и расплавах электролитов. Закон электролиза. Электрический ток в газах. Самостоятельный и несамостоятельный разряды. Понятие о плазме. Ток в вакууме. Электронная эмиссия. Диод. Электронно-лучевая трубка.

Электрический ток в металлах есть движение электронов, ионы металла участия в переносе электрического заряда не принимают. Другими словами, в металлах есть электроны, способные перемещаться по металлу. Они получили название электронов проводимости. Положительные заряды в металле представляют собой ионы, образующие кристаллическую решетку. В отсутствии внешнего поля электроны в металле движутся хаотично, претерпевая соударения с ионами решетки. Под воздействием внешнего электрического поля электроны начинают упорядоченное движение, накладывающееся на их прежние хаотические флуктуации. В процессе упорядоченного движения электроны по-прежнему сталкиваются с ионами кристаллической решетки. Именно этим и обусловлено электрическое сопротивление.

В классической электронной теории металлов предполагается, что движение электронов подчиняется законам классической механики. Взаимодействием электронов между собой пренебрегают, взаимодействие электронов с ионами сводят только к соударениям. Можно сказать, что электроны проводимости рассматривают как электронный газ, подобный идеальному атомарному газу в молекулярной физике. Поскольку средняя кинетическая энергия на одну степень свободы для такого газа равна kT/2, а свободный электрон обладает тремя степенями свободы, то

mv²_t/2=3kT/2,

где v²_t - среднее значение квадрата скорости теплового движения. На каждый электрон действует сила, равная еЕ, в результате чего он приобретает ускорение еЕ/m. Скорость к концу свободного пробега равна

v=eEt/m,

где t - среднее время между соударениями.

Поскольку электрон движется равноускоренно, его средняя скорость равна половине максимальной:

v_c=eEt/(2m).

Среднее время между соударениями есть отношение длины свободного пробега к средней скорости:

t=L/v_t.

Поскольку обычно скорость упорядоченного движения много меньше тепловой скорости, то скоростью упорядоченного движения пренебрегли. Окончательно, имеем

v_c=eEL/(2mv_t).

Коэффициент пропорциональности между v_c и Е называется подвижность электронов.

С помощью классической электронной теории газов могут быть объяснены многие закономерности - закон Ома, закон Джоуля-Ленца и другие явления, однако эта теория не может объяснить, например, явления сверхпроводимости: При определенной температуре удельное сопротивление для некоторых веществ скачком уменьшается практически до нуля. Это сопротивление настолько мало, что однажды возбужденный в сверхпроводнике электрический ток существует длительное время без источника тока. Несмотря на скачкообразное изменение сопротивления, другие характеристики сверхпроводника (теплопроводность, теплоемкость и др.) не меняются либо меняются мало.

Более точным методом, объясняющим такие явления в металлах, является подход с использованием квантовой статистики.