Лабораторная работа3

Министерство высшего и среднего образования РФ.

Государственный Университет Цветных Металлов и Золота.

Кафедра: Физики

Отчёт

Лабораторная работа

по теме: МОДЕЛИРОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ.

Выполнил:

Проверил:

Красноярск 2008г.

МОДЕЛИРОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ

Цель работы: Моделирование и изучение электростатиче­ского поля заряженных тел различной конфигурации.

Оборудование: генератор сигналов низкочастотный ГЭ-109, мультиметр ВР-ПА, кювета с водой, набор электродов различ­ной формы, соединительные провода, металлический щуп-зонд.

Теоретическое введение:

Один из основных законов природы, установленных опытным пу­тем, является закон сохранения электрического заряда. В изолирован­ной системе алгебраическая сумма положительных и отрицательных зарядов остается постоянной. Электрические заряды наделяют окружающее их пространство особыми физическими свойствами, то есть создают электрическое поле, которое проявляется в том, что помещен­ный в это поле пробный заряд испытывает действие силы.

Основными характеристиками поля являются напряженность и потенциал. Напряженностью электрического поля называют отношение силы, действующей на неподвижный точечный заряд, к величине этого заряда:

(1.1)

Этот вектор характеризует каждую точку поля, являясь функцией координат или радиус-вектора точек пространства. Например, поле то­чечного заряда описывается выражением

(1.2)

где - величина заряда, создающего поле; г - радиус-вектор, прове­денный от заряда q до точки наблюдения; E₀- электрическая постоянная,E₀ = 8,85-10"' Ф/м ; ε- диэлектрическая проницаемость среды в данной точке пространства.

Поле, созданное неподвижными зарядами в данной системе от­счета, называется электростатическим. Оно не изменяется с течением времени в каждой точке пространства.

Силовой линией, или линией напряженности электростатического поля, называется линия, в каждой точке которой вектор напряженности направлен по касательной. Линии напряженности поля положительного точечного заряда являются радиальными и исходят из этого заряда. Такое поле называется центральным.

Если имеется система зарядов, то результирующую напряжен­ность можно вычислить, воспользовавшись принципом суперпозиции, который является обобщением большого числа опытных фактов. Этот принцип утверждает, что если по отдельности каждый заряд ^^ создает

поле с напряженностью E, то все они вместе будут создавать поле с

напряженностью E, равной векторной сумме напряженностей, создан­ных каждым зарядом в данной точке:

(1.3)

Соотношения (1.2), (1.3) позволяют вычислить поле для любого расположения неподвижных зарядов. Однако в большинстве случаев это сделать очень трудно, так как, например, в случае непрерывного распределения зарядов необходимо вычислять сложные объемные интегра­лы. Поэтому вычисления напряженностей Ё предоставляют самостоя­тельные задачи, которые осложняются тем, что напряженность поля является векторной величиной. Если поле, созданное непрерывным за­рядом, является симметричным, то, исходя из соображений симметрии, можно определить направление вектора Ё, а величину напряженности найти, используя теорему Остроградского-Гаусса. Например, бесконеч­ная однородно заряженная плоскость создает однородное поле с напря­женностью

(1.4)

где поверхностная плотность заряда. Направлен вектор E по нормали к плоскости. Цилиндр создает центральное неоднородное поле с напряженностью

(1.5)

где линейная плотность заряда;ℓ - расстояние от осевой линии

цилиндра до точки наблюдения.

Силы поля, перемещая точечный заряд, совершают работу, кото­рая зависит от начального и конечного положения заряда в пространст­ве. Работа по замкнутой траектории в этом случае будет равна нулю. Такое поле называется потенциальным. Каждой- точке такого простран­ства можно придать значение потенциальной энергии перемещаемого заряда. Работа поля по перемещению заряда из одной точки поля в дру­гую будет равна разности потенциальных энергий:

(1.6)

Отношение потенциальной энергии IV положительного точечного заряда к величине этого заряда называется потенциалом поля. Тогда разность потенциалов двух точек поля равна отношению работы сил по­ля по перемещению положительного точечного заряда из одной точки в другую к величине этого заряда:

(1.7)

Учитывая, что работа определяется интегрированием внешней си­лы F по перемещениюdℓ, запишем

Откуда получим выражение для разности потенциалов через напряжен­ность электрического поля:

(1.8)

Для центрального поля точечного заряда потенциал рассчитыва­ется по формуле

(1.9)

Разность потенциалов, создаваемая равномерно заряженным цилиндром, определяется по формуле

(1.10)

Геометрическое место точек поля, имеющих один и тот же потен­циал, называют эквипотенциальной поверхностью. Например, эквипо­тенциальными поверхностями поля точечного заряда являются концентрические сферы.

Вектор, направленный в сторону увеличения потенциала по нормали к эквипотенциальной поверхности и равный производ­ной потенциала в этом направле­нии (рис. 1.1), называется градиен­том потенциала и обозначается

(1.11)

где - единичный вектор нормали.

В прямоугольных декартовых координатах градиент потенциала

имеет вид

(1.12)

Как следует из (1.8) , значение позволяет вычислить разность потенциалов и, следовательно, потенциал. Справедливо и обратное ут­верждение. Если во всем пространстве задан потенциал, то можно

вычислить напряженность поля в любой точке. Значит, если точки 1 и 2 располагаются на бесконечно близком расстоянии друг от друга, то для разности потенциалов, по формуле (1.8) имеем

(1.13)

где Ex,Ey,Ez- проекции вектора на направление x,y,z. По определению полного дифференциала

(1.13а)

Сравнивая формулы (1.13) и (1.13, а), находим значения проекций вектора напряженности электрического поля:

(1.14)

Таким образом, при заданном потенциале напряженность

электрического поля вычисляется дифференцированием потенциала по координатам. С учетом (1.11) соотношение. (1.14) можно записать в бо­лее полной форме:

(1.15)

Вместо обозначения gradφ часто используется другое обозначение:

где под знаком « V »(читается «набла») понимается оператор:

Вектор напряженности электрического поля противоположен гра­диенту потенциала, т.е. направлен по нормали к эквипотенциальной по­верхности в сторону уменьшения потенциала.

Графически электрические поля изображают при помощи сило­вых линий и эквипотенциальных поверхностей. Силовые линии реко­мендуется проводить сплошными линиями, эквипотенциальные поверх­ности - пунктирными. Силовые линии и эквипотенциальные поверхно­сти взаимно перпендикулярны, причем эквипотенциальные поверхности проводят так, чтобы значения потенциалов соседних поверхностей отли­чались на одно и то же значение, допустим, на 1В, а число силовых ли­ний на единицу площади было бы пропорциональным модулю напря­женности поля.

Описание установки:

Для исследования электрического поля необходимо собрать уста­новку, схема которой приведена на рис. 1.2.

В кювету. К, заполненную на 1/3 водой, помещают тонкий лист пластика, на котором лежит лист белой бумаги. На бумагу устанавлива­ют электроды Э_1и Э₂. На клеммы1 и 2 подводится напряжение от гене­ратора. Для определения потенциала используют мультиметр. Зонд - металлический стержень с заостренным концом. В работе исследуются поля, созданные следующими конфигурациями электродов (рис. 1.3).

Порядок выполнения работы:

1. Собрать электрическую цепь по схеме (рис. 1.2), после провер­ки преподавателем или лаборантом включить ее.

2. Погрузить на дно кюветы лист бумаги. Установить электроды (по указанию преподавателя). Отметить положения электродов.

3. Измерить разность потенциалов между электродами Э₁

и Э₂ при помощи вольтметра и зонда 2, прикоснувшись зондом к элек­тродам Э₁ и Э₂. Зонд ставить вертикально!

4. Рассчитать разность потенциалов между соседними эквипотен­циальными поверхностями по формуле

где N- выбранное или указанное преподавателем число эквипотенци­альных поверхностей между электродами Э₁ и Э₂.

5. Найти и изобразить ряд точек (не менее 7-10) эквипотенциаль­ной поверхности с потенциалом, равным, при помощи зонда и вольтметра. Держа зонд вертикально, перемещать его осторожно от электрода Э₁ до тех пор, пока на табло вольтметра не появится значение φ₁. Отметить карандашом или ручкой положение зонда.

6. Затем найти и изобразить аналогично п. 5 точки эквипотенци­альных поверхностей с потенциалами

7. Достать лист бумаги и положить его на просушку. Погрузить на дно кюветы новый лист бумаги.

8. При тех же положениях электродов Э₁ и Э₂ поместить между ними металлическое кольцо. Обвести кольцо и электроды. Измерить потенциал электрического поля внутри этого кольца, поместив внутрь кольца зонд 2. Убедившись, что потенциал поля во всех точках внутри кольца и на его поверхности один и тот же, найти и изобразить точки поля с таким же потенциалом за пределами кольца.

9. Достать из кюветы лист бумаги и положить его на просушку. Погрузить на дно новый лист бумаги.

10. Установить в кювете другие электроды (по указанию препода­вателя). Найти и изобразить точки эквипотенциальных поверхностей аналогично пп. 3-7.

Обработка результатов измерений:

1. На всех листах бумаги с изображенными контурами электродов и точками эквипотенциальных поверхностей необходимо провести через все точки пунктирные линии и записать у каждой этой линии соответст­вующие значение потенциала поля.

2. Построить систему силовых линий, проведя сплошные линии перпендикулярно эквипотенциальным поверхностям (пунктирными ли­ниями). Указать направление силовых линий в сторону уменьшения по­тенциала.

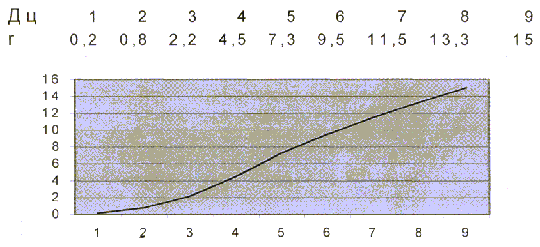
3. Используя изображения поля между плоскопараллельными, электродами, построить график зависимости потенциала поля φ от рас­стояния r , отсчитываемого от электрода Э₁. По графику определить на­пряженность" поля, которая пропорциональна тангенсу угла наклона и

равна градиенту потенциала:

4. Используя изображение поля с металлическим кольцом, опре­делить напряженность поля внутри кольца по градиенту потенциала.

Сделать вывод о характере электрического поля внутри металла, поме­щенного во внешнее поле.

5. Используя изображение поля, созданного двумя цилиндриче­скими электродами, определить поверхностную плотность зарядов на электродах.

6. Рассчитать напряженность электрического поля в произвольной точке, указанной преподавателем, для любой конфигурации электродов.

Формулы для вычислений:

Δφ=Δφ_max/(N+1);E=-Δφ/Δr,Δφ_max=9В, Δφ=9/(8+1)=1В, E=-10В/М.