
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА . |
3
|
|
§ 1. |
Определение определённого интеграла…………………………….. |
5 |
§ 2. |
Длина дуги кривой…………………………………………………… |
11 |
§ 3. |
Площадь криволинейной трапеции…………………………………. |
14 |
§ 4. |
Площадь поверхности вращения……………………………………. |
17
|
Заключение…………………………………………………………………. |
19
|
|
Литература…………………………………………………………………… |
21 |
|
Введение. Мною была выбрана курсовая работа по теме «Определенный интеграл. Приложения определенного интеграла», в связи с этим, я решила узнать, откуда появился этот загадочный значок интеграл, почему так называется и такую большую роль играет в математике.
ИНТЕГРАЛ одно из важнейших понятий математики, возникшее в связи с потребностью, с одной стороны отыскивать функции по их производным (например, находить функцию, выражающую путь, пройденный движущейся точкой, по скорости этой точки), а с другой - измерять площади, объемы, длины дуг, работу сил за определенный промежуток времени и т. п.
Символ
![]() введен
Лейбницем
(1675 г.). Этот
знак является изменением латинской
буквы S
(первой буквы
слова сумма).
Само слово интеграл
придумал Я.
Бернулли (1690 г.).
Вероятно,
оно происходит от латинского integero,
которое переводится, как приводить
в прежнее состояние, восстанавливать.
Действительно,
операция интегрирования “восстанавливает”
функцию, дифференцированием которой
получена подынтегральная функция.
Возможно происхождение слова интеграл
иное: слово integer
означает целый.
В 1696г.,
появилось название новой ветви математики
- интегральное
исчисление
(calculus
integralis),
которое ввел И.
Бернулли.
введен
Лейбницем
(1675 г.). Этот
знак является изменением латинской
буквы S
(первой буквы
слова сумма).
Само слово интеграл
придумал Я.
Бернулли (1690 г.).
Вероятно,
оно происходит от латинского integero,
которое переводится, как приводить
в прежнее состояние, восстанавливать.
Действительно,
операция интегрирования “восстанавливает”
функцию, дифференцированием которой
получена подынтегральная функция.
Возможно происхождение слова интеграл
иное: слово integer
означает целый.
В 1696г.,
появилось название новой ветви математики
- интегральное
исчисление
(calculus
integralis),
которое ввел И.
Бернулли.
В современной
литературе множество всех первообразных
для функции f(x)
называется также неопределенным
интегралом.
Это понятие выделил Лейбниц,
который заметил, что все первообразные
функции
отличаются на произвольную постоянную.
А
![]() называют определенным
интегралом
(обозначение
ввел К. Фурье (1768-1830),
но пределы
интегрирования указывал уже Эйлер).
называют определенным
интегралом
(обозначение
ввел К. Фурье (1768-1830),
но пределы
интегрирования указывал уже Эйлер).
Возникновение задач интегрального исчисления связано с нахождением площадей и объемов.
Однако при всей значимости результатов, полученных математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно точный алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный нам под названием формулы Ньютона - Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.
Строгое изложение теории интеграла появилось только в прошлом веке, Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков, немецкого ученого Б. Римана (1826 - 1866 гг.), французского математика Г. Дарбу (1842 - 1917).
§ 1. ОПРЕДЕЛЕНИЕ
ОПРЕДЕЛЁННОГО ИНТЕГРАЛА. Пусть
в интеграле
![]() нижний предел а = const,
а верхний предел b
изменяется. Очевидно, что если изменяется
верхний предел, то изменяется и значение
интеграла. Обозначим
нижний предел а = const,
а верхний предел b
изменяется. Очевидно, что если изменяется
верхний предел, то изменяется и значение
интеграла. Обозначим
![]() = f(х).
Найдем производную функции f(х)
по переменному верхнему пределу х.
= f(х).
Найдем производную функции f(х)
по переменному верхнему пределу х.
![]() Аналогичную теорему можно доказать для
случая переменного нижнего предела.
Аналогичную теорему можно доказать для
случая переменного нижнего предела.
ТЕОРЕМА 1: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема 2:
(Теорема Ньютона – Лейбница) Если
функция F(x)
– какая- либо первообразная от непрерывной
функции f(x),
то:
![]() это выражение известно под названием
формулы Ньютона–Лейбница.
это выражение известно под названием
формулы Ньютона–Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
![]()
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:
![]()
![]()
![]()
Тогда
![]() .
.
А при х = b:
![]()
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
Теорема доказана.
Иногда применяют обозначение F(b)
– F(a)
= F(x)![]() .
.
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Определение. Если существует конечный передел интегральной суммы (1)
![]() - (1)
- (1)
при λ→0, не зависящий от способа разбиения τn отрезка [a; b] на частичные отрезки и выбора промежуточных точек ξk, то этот предел называют определенным интегралом (или интегралом Римана) от функции f(x) на отрезке [a; b] и обозначают:
![]()
Если указанный предел существует, то функция f(x) называется интегрируемой на отрезке [a; b] (или интегрируемой по Риману). При этом f(x)dx называется подынтегральным выражением, f(x) – подынтегральной функцией, х – переменной интегрирования, a и b – соответственно нижним и верхним пределами интегрирования.
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения λ стремится к нулю.
Условия существования определенного интеграла
1) Интегрируемая функция необходимо ограничена.
Если
бы функция f(x)
была в промежутке [a,
b]
неограниченна, то – при любом разбиении
промежутка на части – она сохранила бы
подобное свойство хоть в одной из частей.
Тогда за счет выбора в этой части точки
![]() можно было бы сделать f(
),
а с ней и сумму
можно было бы сделать f(
),
а с ней и сумму
![]() ,
- сколь угодно большой; при этих условиях
конечного предела для
существовать не могло бы.
,
- сколь угодно большой; при этих условиях
конечного предела для
существовать не могло бы.
2) Для существования определенного интеграла необходимо и достаточно, чтобы было
![]() (S
- s) = 0 s
=
(S
- s) = 0 s
=
![]() m
m![]() ΔX
ΔX![]() , S
=
M
ΔX
,
, S
=
M
ΔX
,
где m и M - точные нижняя и верхняя грани. Суммы Дарбу s и S служат точными, соответственно, нижней и верхней границами для интегральных сумм.[6]
Основные свойства определенного интеграла:
1. Если нижний и верхний пределы интегрирования равны (a=b), то интеграл равен нулю:
![]() Это
свойство следует из определения
интеграла.
Это
свойство следует из определения
интеграла.
Если f(x)=1, то
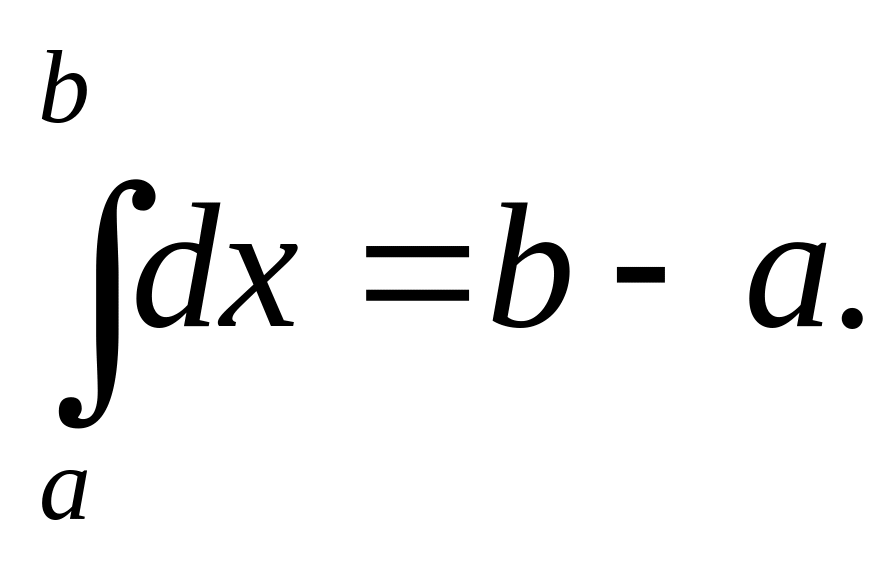
Действительно,
так как f(x)=1,
то
![]()
При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
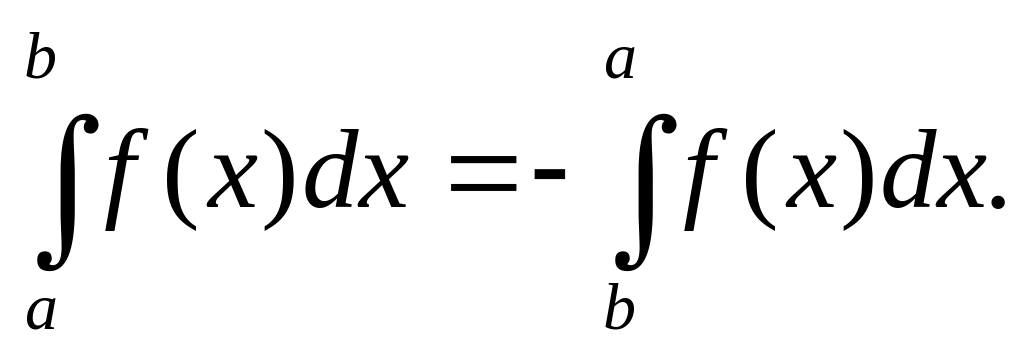
Постоянный множитель можно выносить за знак определенного интеграла:
![]()
![]() R.
R.
Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f1(x), f2(x), …, fn(x) равен алгебраической сумме определенных интегралов от слагаемых:
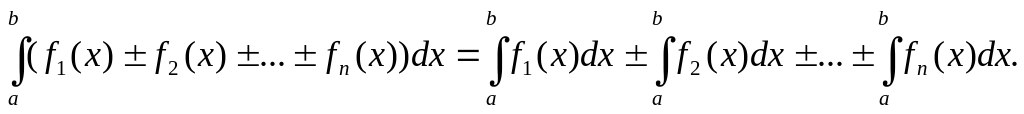
6. (аддитивность
определенного интеграла). Если
существуют интегралы
![]() и
и
![]() то существует также интеграл
и для любых чисел a,
b,
c;
то существует также интеграл
и для любых чисел a,
b,
c;
![]()
7.
Если
f(x) ≥ 0
![]() [a;
b], то
[a;
b], то
![]() a
< b.
a
< b.
8
. (определенность
определенного интеграла). Если
интегрируемые функции f(x)
и φ(x)
удовлетворяют неравенству f(x)
≥ φ(x)
[a;
b],
то
![]() a
>b.
a
>b.
9 . (об оценке определенного интеграла). Если m и М – соответственно наименьшее и наибольшее значения функции f(x), непрерывной на отрезке [a; b], то
![]() a
< b.
a
< b.
10. (теорема
о среднем). Если
функция f(x)
непрерывна на отрезке [a;
b],
то существует такая точка
![]() [a;
b],
что
[a;
b],
что
![]()
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [a; b] и длины b-a этого отрезка.[10]
Пример 1.
![]() .
.
Пример 2.
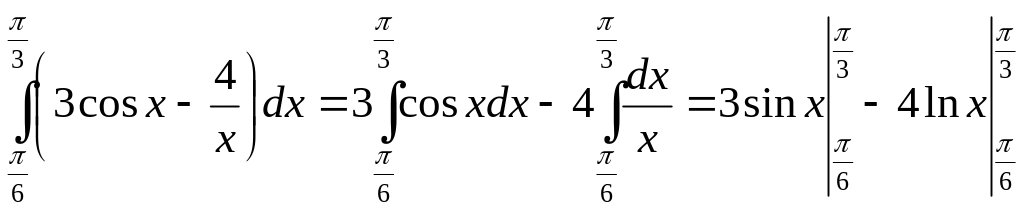
![]()
§ 2. Длина дуги кривой. Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y=f(x), где a ≤ x ≤ b. (рис1).
Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю.
Применим схему I (метод сумм).
Точками X
 = a,
X
= a,
X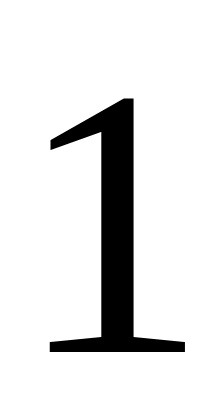 ,
… , X
,
… , X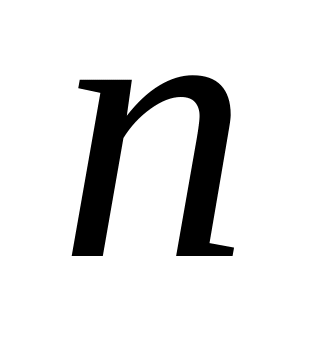 = b
(X
≤ X
≤
… ≤ X
)
разобьем отрезок [a,
b]
на n
частей. Пусть этим точкам соответствуют
точки M
= A,
M
= b
(X
≤ X
≤
… ≤ X
)
разобьем отрезок [a,
b]
на n
частей. Пусть этим точкам соответствуют
точки M
= A,
M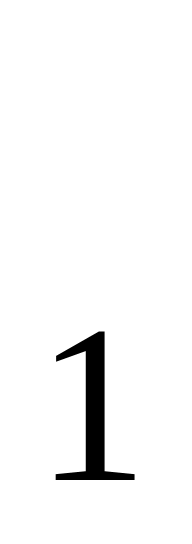 , … , M
, … , M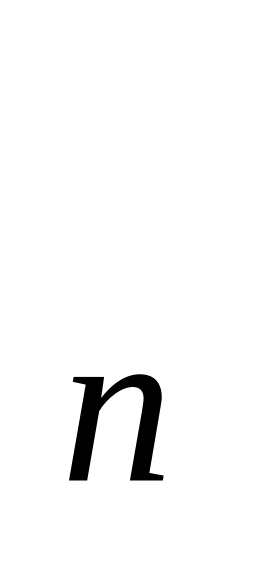 = B
на кривой AB.
Проведем хорды M
M
,
M
M
= B
на кривой AB.
Проведем хорды M
M
,
M
M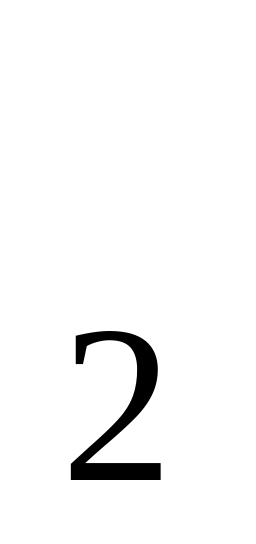 ,
… , M
,
… , M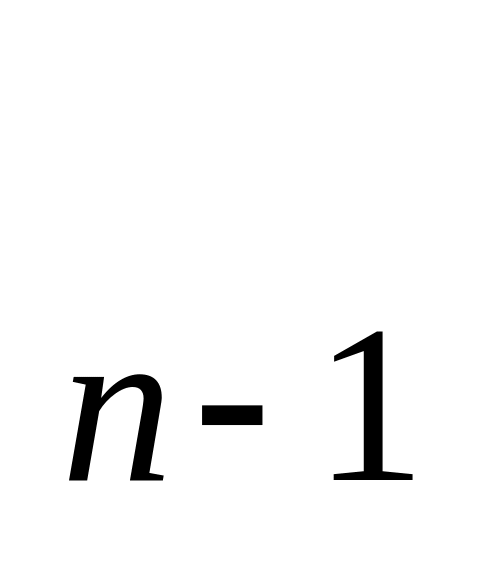 M
, длины которых обозначим соответственно
через ΔL
,
ΔL
,
… , ΔL
.
M
, длины которых обозначим соответственно
через ΔL
,
ΔL
,
… , ΔL
.
Рис 1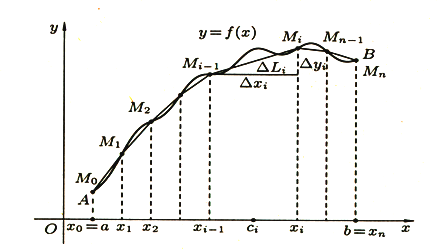
Получим
ломанную M
M
M
… M
M
,
длина которой равна L
= ΔL
+
ΔL
+
… + ΔL
=
![]() ΔL
.[6]
ΔL
.[6]
Длину хорды (или звена ломанной) ΔL можно найти по теореме Пифагора из треугольника с катетами ΔX и ΔY :
ΔL
=
![]() ,
где ΔX
= X
,
где ΔX
= X![]() - X
- X![]() ,
ΔY
= f(X
)
– f(X
).
,
ΔY
= f(X
)
– f(X
).
По
теореме Лагранжа о конечном приращении
функции ΔY
=
![]() (C
)
ΔX
,
где C
(C
)
ΔX
,
где C
![]() (X
,
X
).
(X
,
X
).
Поэтому
ΔL
=
![]() =
=
![]() , а длина всей ломанной M
M
M
… M
M
равна
, а длина всей ломанной M
M
M
… M
M
равна
L = ΔL = .
Длина
кривой AB,
по определению, равна L
=
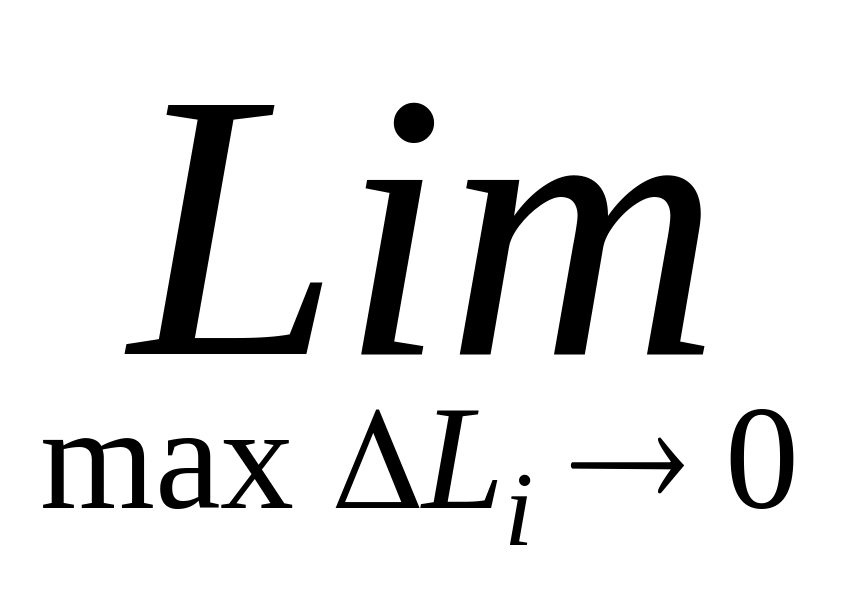 L
=
ΔL
.
Заметим, что при ΔL
L
=
ΔL
.
Заметим, что при ΔL
![]() 0 также и ΔX
0 (ΔL
=
и следовательно | ΔX
| < ΔL
).
Функция
0 также и ΔX
0 (ΔL
=
и следовательно | ΔX
| < ΔL
).
Функция
![]() непрерывна на отрезке [a,
b],
так как, по условию, непрерывна функция
f
непрерывна на отрезке [a,
b],
так как, по условию, непрерывна функция
f![]() (X).
Следовательно существует предел
интегральной суммы
(X).
Следовательно существует предел
интегральной суммы
L = ΔL = , кода max ΔX 0:
L
=
![]() =
=
![]() dx.
dx.
Таким образом, L = dx.
Пример: Найти длину окружности радиуса R. (рис 2)[5]
Решение:
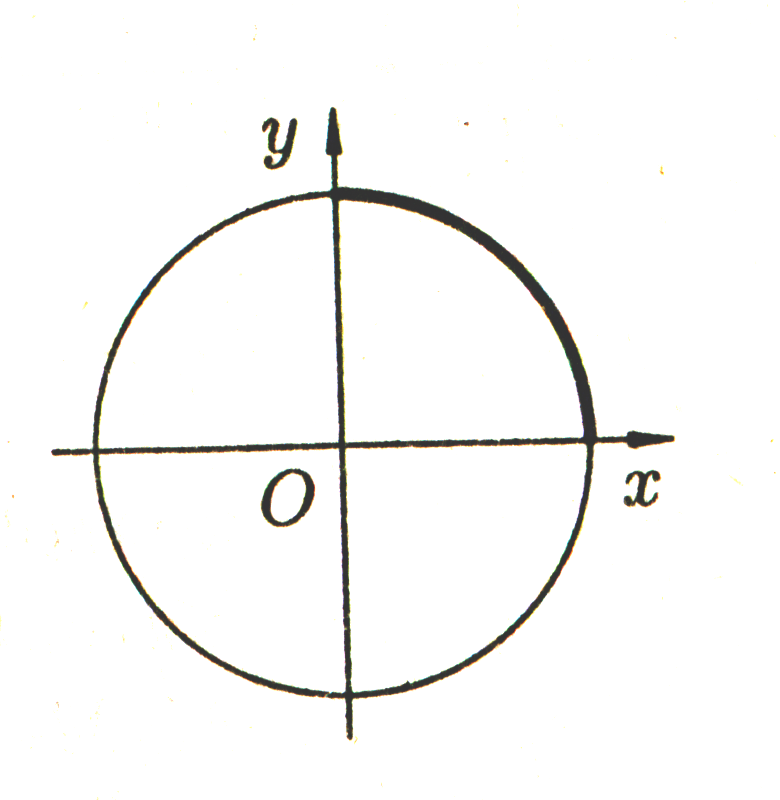 Найдем
¼ часть ее длины от точки (0;R)
до точки (R;0).
Так как y
=
Найдем
¼ часть ее длины от точки (0;R)
до точки (R;0).
Так как y
=
![]() ,
¼L
=
,
¼L
=
![]()
![]() dx
= R
arcsin
dx
= R
arcsin![]()
![]() = R
= R
![]() .
.
Рис 2
Значит
L
= 2![]() R.
R.
ПОЛЯРНЫЕ
КООРДИНАТЫ. Пусть
кривая AB
задана уравнением в полярных координатах
r
= r(![]() ),
),
![]() .
Предположим, что r(
)
и r
(
)
непрерывны на отрезке [
.
Предположим, что r(
)
и r
(
)
непрерывны на отрезке [![]() ].
].
Если
в равенствах x
= r
cos
,
y
= r
sin
,
связывающих полярные и декартовы
координаты, параметром считать угол
,
то кривую AB
можно
задать параметрически
![]()
Тогда
![]() Поэтому
Поэтому
![]() =
=
![]() =
=
![]()
П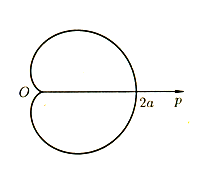 рименяя
формулу L
=
рименяя
формулу L
=
![]() ,
получаем L
=
,
получаем L
=
![]()
![]()
Пример:
Найти
длину кардиоиды Рис 3 r
= a(1
+ cos
).
Рис 4
Решение:
Кардиоида
r
= a(1
+ cos
)
симметрична относительно полярной оси.
Найдем половину длины кардиоиды: ½ L
=
![]()
![]() = a
= a
![]() = a
= a
![]() = 2a
cos
= 2a
cos![]() d
= 4a
sin
d
= 4a
sin
![]() = 4a.
[7]
= 4a.
[7]
