
- •1. Введение в механику сплошной среды
- •1.1. Предмет и метод механики сплошной среды
- •1.2. Плотность распределения гидромеханических характеристик в сплошной среде
- •1.3. Физические свойства жидкостей и газов
- •2. Статика текучего тела (гидростатика)
- •2.1. Гидростатическое давление
- •2.2. Дифференциальные уравнения равновесия текучего тела (уравнения эйлера)
- •2.3. Интегрирование уравнений эйлера
- •2.4. Способы измерения гидростатического давления
- •3. Кинематика сплошной среды
- •3.1. Движение точки с позиций теоретической механики
- •3.2. Методы описания движения сплошной среды
- •3.3. Поток гидромеханической характеристики через поверхность
- •3.4. Гидромеханическая интерпретация теоремы остроградского гаусса
- •3.5. Циркуляция скорости. Вихрь вектора скорости
- •3.6. Поля в гидродинамике
- •3.6.1.Операции над тензорами
- •4. Напряжения и деформации в твёрдых средах
- •4.1. Силы, действующие на текучее тело
- •4.2. Напряжённое состояние в точке сплошной среды. Тензор напряжений
- •4.3. Элементарные деформации. Коэффициент пуассона
- •Напряжений, действующих на грани кубика
- •5.2. Напряжения и деформации в твёрдых средах с точки зрения геодинамики
- •5.3. Упругие деформации
- •5.3.1.Соотношения линейной теории упругости
- •Одноосного сжатия
- •6. Основы гидродинамики
- •6.1. Основные положения
- •Закон сохранения массы;
- •6.2.Закон сохранения массы
- •6.3. Закон изменения количества движения
- •6.4. Закон изменения момента количества движения
- •6.5. Закон изменения кинетической энергии
- •6.6. Закон сохранения энергии для контрольного объёма сплошной среды
- •6.7. Уравнения движения и равновесия
- •7. Теоретические основы решения одномерных задач
- •7.1. Основные термины и понятия
- •7.2. Уравнение бернулли для установившегося напорного потока вязкой жидкости
- •7.3. Геометрическая и энергетическая интерпретации слагаемых, входящих в уравнение бернулли
- •7.4. Потенциальный и полный (гидродинамический) напоры. Пъезометрическая и напорная линии
- •8. Основы реологии
- •8.1. Уравнения состояния идеальных и реальных жидкостей
- •8.2. Моделирование движения сложных сред
- •8.2.1. Течение ньютоновской жидкости в круглой трубе
- •8.2.2. Неньютоновские жидкости
- •8.2.3.Механические модели неньютоновских сред
- •9. Движение жидкостей и газов в пористой среде
- •9.1.Основные понятия
- •9.2.Определение эффективного диаметра
- •9.3.Формулы фильтрации
- •10. Базовые задачи гидродинамики, используемые в нефтегазовой отрасли
- •10.1. Постановка задач
- •10.2. Ламинарное и турбулентное течение жидкостей в щелевом канале
- •10.3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
3.4. Гидромеханическая интерпретация теоремы остроградского гаусса
Зафиксируем
неподвижную в пространстве контрольную
поверхность А, ограничивающую контрольный
объём V.
Сквозь эту поверхность протекает
жидкость со скоростью
![]() .
Выделим на ней элементарную площадку
dА. Единичный вектор нормали к площадке
.
Выделим на ней элементарную площадку
dА. Единичный вектор нормали к площадке
![]() . Если воспользоваться ортами i,
j,
k
, то
. Если воспользоваться ортами i,
j,
k
, то
![]() .
.
Обозначим модуль
скорости
![]() ;
по определению
;
по определению
![]() .
Скалярное произведение двух векторов
можно выразить через их проекции:
.
Скалярное произведение двух векторов
можно выразить через их проекции:
![]() ,
(3.4.1)
,
(3.4.1)
а также через модули векторов и угол между ними,
![]() (3.4.2)
(3.4.2)
где un нормальная к поверхности dА составляющая скорости.
Таким образом,
![]() .
(3.4.3)
.
(3.4.3)
Используя (3.4.3), запишем объёмный расход жидкости Q через поверхность dА:
 . (3.4.4)
. (3.4.4)
Согласно теореме Остроградского Гаусса имеем
![]() . (3.4.5)
. (3.4.5)
Рис. 3.8. Определение
расхода жидкости сквозь поверхность
элементарного параллелепипеда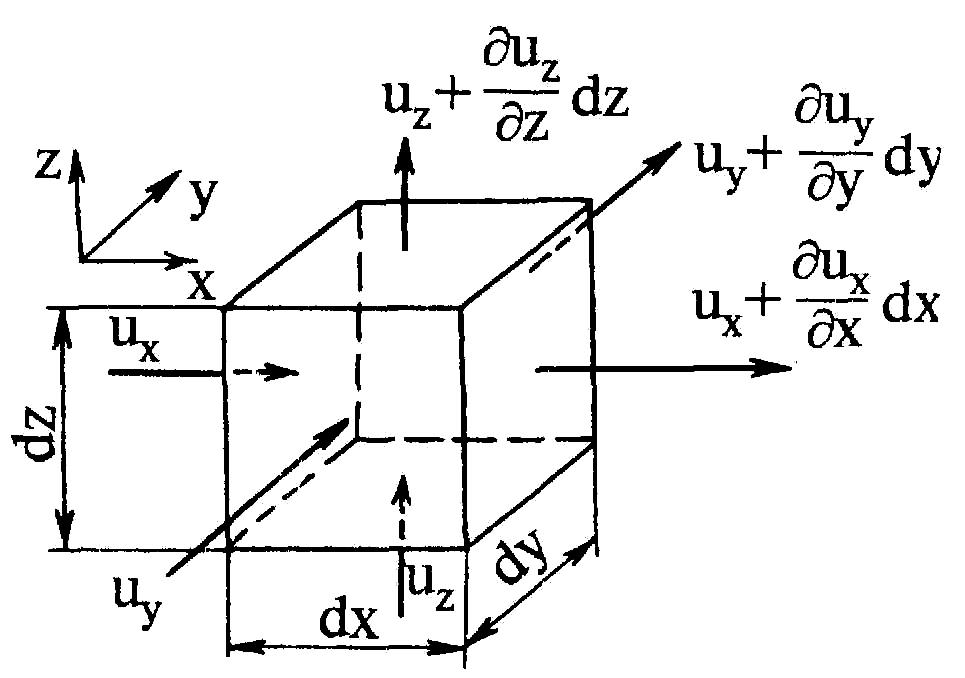
Зафиксируем в пространстве параллелепипед с бесконечно малыми рёбрами dx, dy, dz , поверхностью iА и объёмом iV = dxdydz.
На каждой грани параллелепипеда значение un вследствие её малости постоянно и равно проекции скорости на координатную ось, к которой эта грань нормальна.
Пусть проекции
скорости имеют направления, указанные
на рисунке. Расход жидкости
![]() ,
протекающий сквозь поверхность iА,
определим как разность между объёмом
жидкости, вытекающей из параллелепипеда
в единицу времени:
,
протекающий сквозь поверхность iА,
определим как разность между объёмом
жидкости, вытекающей из параллелепипеда
в единицу времени:
![]()
и объём жидкости, втекающей в него за то же самое время:
![]() .
.
В результате имеем

или
![]() ,
(3.4.6)
,
(3.4.6)
где div u дивергенция вектора скорости, которая определяет собой скалярную величину, определяемую равенством
![]() .
(3.4.7)
.
(3.4.7)
Если жидкость несжимаемая, то из закона сохранения массы следует, что объём жидкости, втекающей в элементарный объём iV равен объёму жидкости, вытекающей из него, так что
![]() .
(3.4.8)
.
(3.4.8)
Поскольку объём не может быть равным 0, из уравнения (3.4. 6) следует, что в случае несжимаемой жидкости
div u = 0. (3.4.9)
Уравнение (2.4.9) называют уравнением несжимаемости жидкости. Оно справедливо в случае неустановившегося движения жидкости, когда для каждого момента времени и в каждой точке потока.
Чтобы обобщить равенство (3.4.6) для произвольного объёма V , ограниченного произвольной поверхностью А (рис.3.9.) разобьём V на элементарные параллелепипеды. Для каждого из них можно записать равенство (3.4. 6).
Рис.3.9. Определение
расхода сквозь произвольную
контрольную поверхность
![]() ,
которые относятся к тем граням элементарных
параллелепипедов, которые совпадают с
контрольной поверхностью А. Следовательно,
в левой части сумма интегралов, относящихся
ко всем параллелепипедам, будет равна
,
которые относятся к тем граням элементарных
параллелепипедов, которые совпадают с
контрольной поверхностью А. Следовательно,
в левой части сумма интегралов, относящихся
ко всем параллелепипедам, будет равна
![]() . (3.4.10)
. (3.4.10)
В правой части суммы всех уравнений (3.4. 6) по определению интеграла как предела суммы бесконечно малых слагаемых имеем
![]() (3.4.11)
(3.4.11)
Таким образом, для объёма V произвольной формы справедливо равенство
![]() (3.4.12)
(3.4.12)
Представив
![]() ,
получим
,
получим
![]() ,
,
что и составляет содержание теоремы Гаусса Остроградского.
