3.2. Методы описания движения сплошной среды

Рис. 3.1. Скорость и ускорение материальной точки. Пунктиром показана её траектория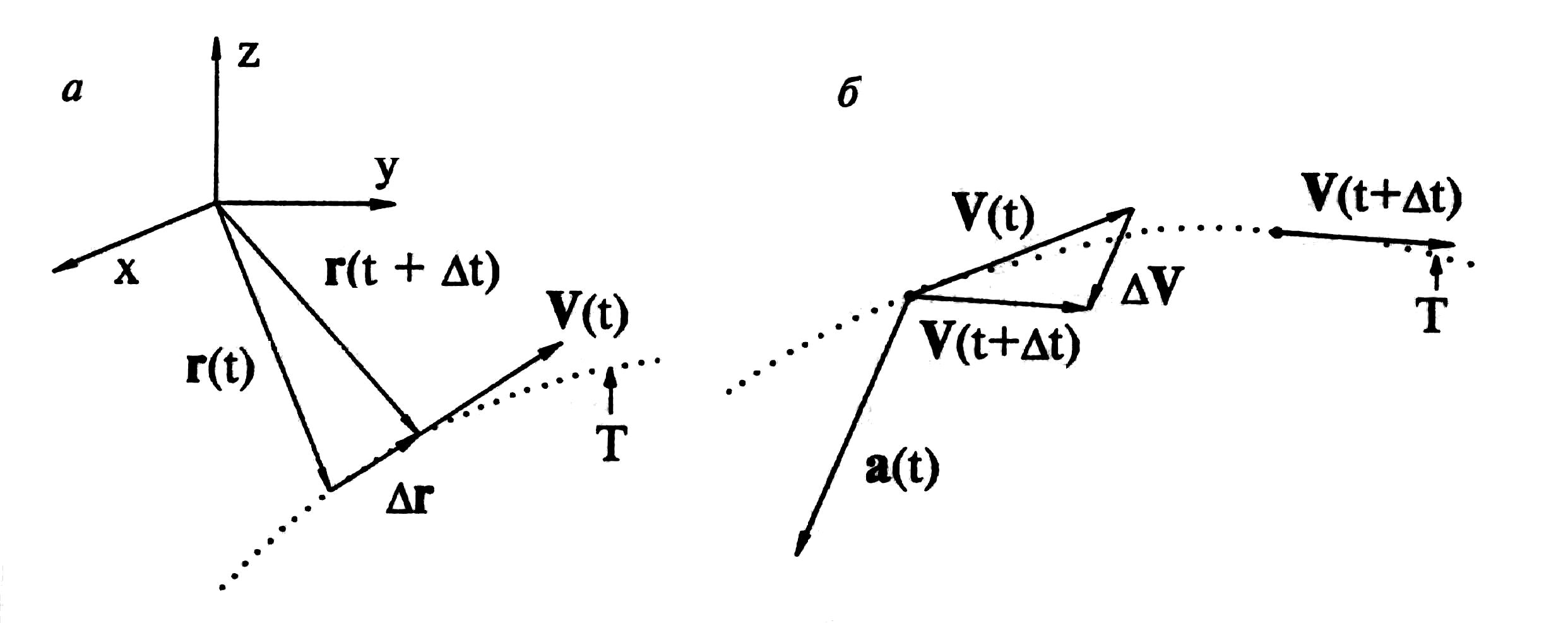

При изучении движения сплошной среды можно также выделить бесконечно малые объёмы, положение которых характеризуется в пространстве тремя координатами или величиной одного радиус-вектора , и рассматривать движение сплошной среды как движение совокупности взаимно связанных и взаимодействующих бесконечно малых (точечных) объёмов.

Метод Лагранжа. Обозначим координаты начального (в момент времени ) положения каждой точки сплошной среды через . Для полного описания движения сплошной среды необходимо знать траектории движения всех частиц, т.е. положение каждой частицы в любой момент времени . Это означает, что для каждой частицы надо знать уравнение её траектории . При этом одну частицу от другой отличает начальное положение частицы, и, следовательно, величина войдёт в уравнение траектории жидкой частицы как параметр:

Рис.3.2. Задание координат методом Лагранжа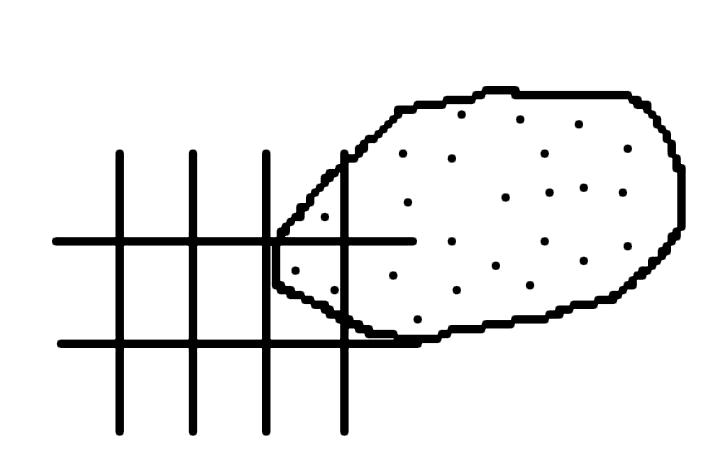

. (3.2.1)

Такой подход к описанию движения сплошной среды называется методом Лагранжа, а характеристики сплошной среды (скорость, плотность, давление и т.п.), связанные с движущимися элементарными объёмами сплошной среды, равно как и координаты этого объёма, называются лагранжевыми переменными.

Лагранжевы координаты  это параметры, которые характеризуют каждую точку среды и не меняются в процессе. Таким образом, точка зрения Лагранжа опирается на описание истории движения каждой точки сплошной среды в отдельности. Такое описание на практике оказывается слишком подробным и сложным, оно всегда подразумевается при формулировке физических законов.

Используя равенства, введённые в теоретической механике

,

можно вычислить скорость и ускорение каждой частицы, а затем, определив величину внешних (поверхностных и объёмных) сил, действующих на каждую частицу, записать уравнения движения для сплошной среды.

Несмотря на кажущуюся простоту метода Лагранжа, уравнения движения, получаемые на основе этого метода, очень сложны, и он используется сравнительно редко.

Более удобен и потому гораздо шире используется другой подход к описанию движения сплошной среды, называемый методом Эйлера.

Согласно этому методу фиксируют не частицы жидкости, а точки пространства, через которые проходят в разные моменты времени различные элементарные объёмы жидкости, т.е. жидкие частицы. В этих точках определяются значения скорости движения сплошной среды. Таким образом, средством описания движения сплошной среды является поле скорости движения жидких частиц в фиксированных точках пространства:

. (3.2.2)

Характеристики сплошной среды (поле скорости, поле давлений, поле напряжений и т.п.), отнесённые к фиксированным неподвижным элементам геометрического пространства (точкам, линиям, поверхностям, объёмам), и сами эти элементы называют эйлеровыми переменными.

Этот метод удобен благодаря следующим преимуществам.

• Во-первых, наблюдать за движущимися (например, в трубе) фиксированными (мечеными) жидкими частицами значительно сложнее, чем за характеристиками движения сплошной среды.

• Во-вторых, соответствующие этому методу уравнения оказываются проще для анализа.

Подчеркнём, что, если в методе Лагранжа  это искомые функции времени, то в методе Эйлера пространственные координаты  не функции времени, а независимые переменные, декартовы координаты пространства, в котором перемещается сплошная среда. Искомыми переменными являются скорость и давление .

Учитывая, что в методе Эйлера описание движения отличается от принятого в теоретической механике, существуют некоторые отличия в определении ускорения, которое входит во второй закон Ньютона. В это уравнение входит ускорение материальной точки, которое для сплошной среды определяется, как и в теоретической механике, второй производной пути по времени только при использовании метода Лагранжа. В случае метода Эйлера ускорение, а также другие гидромеханические величины, которые меняются вместе с движением объёма жидкости, выражаются через специальный вид производной, которая определённым образом связана с полем скорости (3.2.2). Вместе с тем эта производная должна быть связана с движением частиц жидкости или газа (субстанции). Такую производную называют полной или субстанциальной.

Скорость. Пусть некоторая точка сплошной среды в момент t находится в точке М пространства, а в момент t + t в точке M´, и . r  малое направленное перемещение индивидуальной точки сплошной среды за время t (если в пространстве можно ввести радиус-вектор, то это приращение радиус-вектора рассматриваемой точки сплошной среды). Предел отношения двух соответствующих бесконечно малых количеств r и t при t 0 (в случае неевклидова пространства) или частная производная радиуса-вектора точки сплошной среды относительно системы отсчёта по времени (в случае евклидова пространства) называется скоростью точки сплошной среды.

Радиус-вектор r зависит в общем случае от трёх параметров x, y, z , индивидуализирующих точку сплошной среды, и времени t. Скорость вычисляется для индивидуальной точки сплошной среды, т.е. при фиксированных x, y, z , поэтому и берётся частная производная от r по t: . Бесконечно малое перемещение точки сплошной среды можно разложить по векторам базиса, взятым в точке М:

r = xi + yj + zk,

где x, y, z являются компонентами перемещения r. Или, переписывая в обобщённом и сокращённом виде, будем иметь

r =  xⁱ е_i = xⁱ е_i (*)

(В последнем выражении знак суммы опущен).

Поделив (*) на элемент времени t, соответствующий перемещению точки сплошной среды из точки М в точку M´ пространства наблюдателя, и взяв предел при t 0 , получим по определению скорость точки сплошной среды : ,

откуда ,

индексы внизу указывают на то, что производные берутся при постоянных параметрах, индивидуализирующих точку среды. Величины v_x, v_y, v_z называются компонентами вектора скорости v в базисе i, j, k. Скорость и её компоненты зависят от x, y, z, t:

v_x = v_x (x, y, z, t),

v_y = v_y (x, y, z, t),

v_z = v_z (x, y, z, t).

Запишем проекции скоростей и ускорений точек среды на обобщённые оси координат х_i, которые определяются обычными равенствами:

,

. (3.2.3)

Таким образом, в методе Эйлера задаются перемещение, скорость, ускорение в точке пространства (неподвижная система отсчёта), мимо которой в данный момент проходят частицы среды как функции координат точек пространства x_i и времени t:

u_i = u_i (x₁, x₂, x₃ , t);

v_i = v_i (x₁, x₂, x₃ , t);

а_i = a_i (x₁, x₂, x₃ , t). (3.2.4)

Совокупность параметров х_i и t называют переменными Эйлера.

Ввиду того, что в механике сплошной среды могут встретиться оба метода, необходимо научиться осуществлять переход от одних переменных к другим.

Переход от переменных Лагранжа к переменным Эйлера. Предположим, что у нас всё известно о среде с точки зрения Лагранжа, то есть, мы имеем и закон движения в соответствующей форме:

Для того, чтобы перейти к переменным Эйлера нам необходимо:

• разрешить уравнения относительно _i. При фиксированных координатах х_i эти соотношения указывают те точки _i сплошной среды, которые в разные моменты времени проходят через данную точку пространства.

_i = _i(x₁, x₂, x₃ , t)

или

(3.2.5)

• подставить это в выражения по Эйлеру:

.

Рис. 3.3. Переход от координат Эйлера к координатам Лагранжа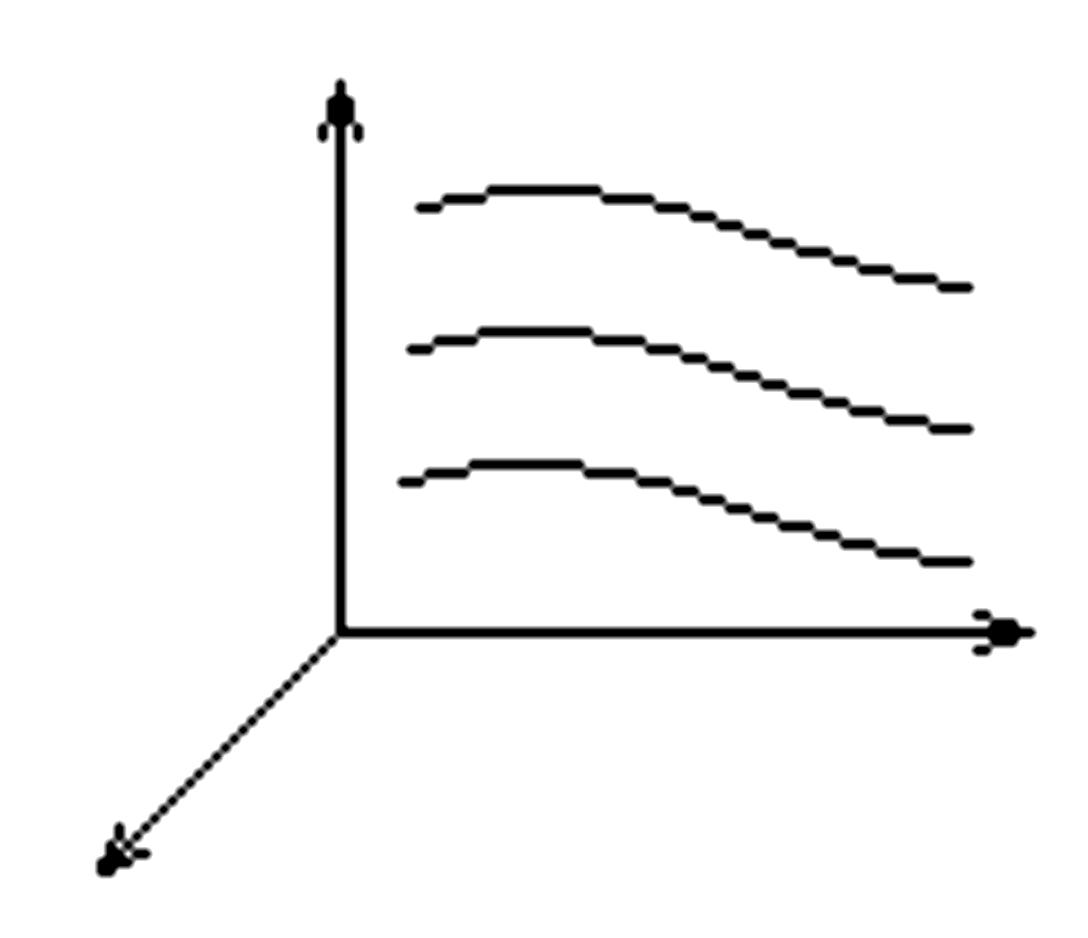

Для перехода от переменных Эйлера к переменным Лагранжа имеем:

(*), проекция которой на ось х₂ равна , а проекция на ось х₃ равна .

Для начальных условий при t = 0:

,

откуда

• получим систему обыкновенных дифференциальных уравнений относительно х_i: или

• Решая эту систему, определим х_i = х_i(С₁, С₂, С₃, t), где  С₁, С₂, С₃  постоянные, определяемые по х_i при t = t_0;

• подставив (**) в (*), получим лагранжевы координаты.

.

Ускорение и его вычисление по скорости. Ускорение – это скорость изменения скорости индивидуальной частицы. Если скорость задана по Лагранжу, т.е.

.

Если скорость задана по Эйлеру, то В индивидуальной частице:

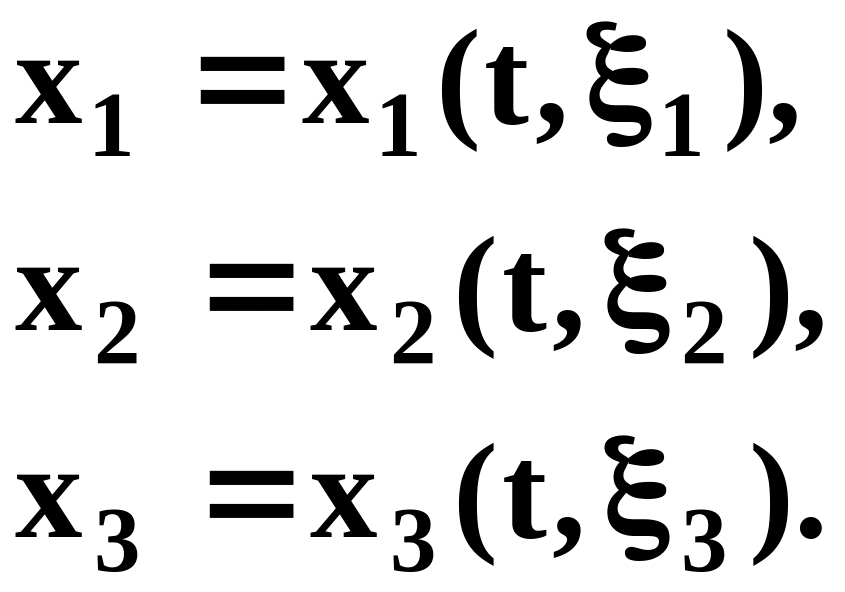
Поэтому по формуле дифференцирования сложной функции

Окончательная формула по Эйлеру будет выглядеть:

.

Это полная (материальная) производная скорости по времени, индивидуальная производная по времени, субстанциальная производная.

По Эйлеру производная по времени при x_i = const – изменение скорости по времени в данном месте пространства – локальная производная по времени.

Если =0, то движение установившееся (стационарное):

.

В декартовых координатах x,y,z:

.

В проекциях

;

;

.

Материальная (полная) или индивидуальная производная по t от любой величины (например, плотности ) определится следующим образом:

• Если используется способ Лагранжа, т.е. если , то индивидуальная производная есть частная .

• Если используется способ Эйлера, т.е. , то индивидуальная производная есть

или = .

Для несжимаемой среды , при этом может быть и не равно 0 (т.к.среда неоднородная).

Таким образом, если функция задана в переменных Эйлера:  =  (x₁, x₂, x₃, t), необходимо

• перейти к переменным Лагранжа;

• воспользоваться правилом дифференцирования сложной функции, в результате чего получим

. (3.2.6)

Производная называется полной производной (индивидуальной, субстанциальной) и характеризует изменение плотности данной частицы сплошной среды в единицу времени. Производная называется частной (местной, локальной) и характеризует изменение плотности в данной точке пространства в единицу времени. Величина называется конвективной производной.

Рассмотрим полную производную по времени от температуры. По Эйлеру это будет выглядеть следующим образом:

.

Физический смысл (по Эйлеру) – это производная температуры по времени в какой-либо фиксированной точке пространства x = const. В координатах Лагранжа . Физический смысл (по Лагранжу)  производная по времени температуры какой-то частицы, где бы она ни находилась.

Рис.3.4. Векторные линии или линии тока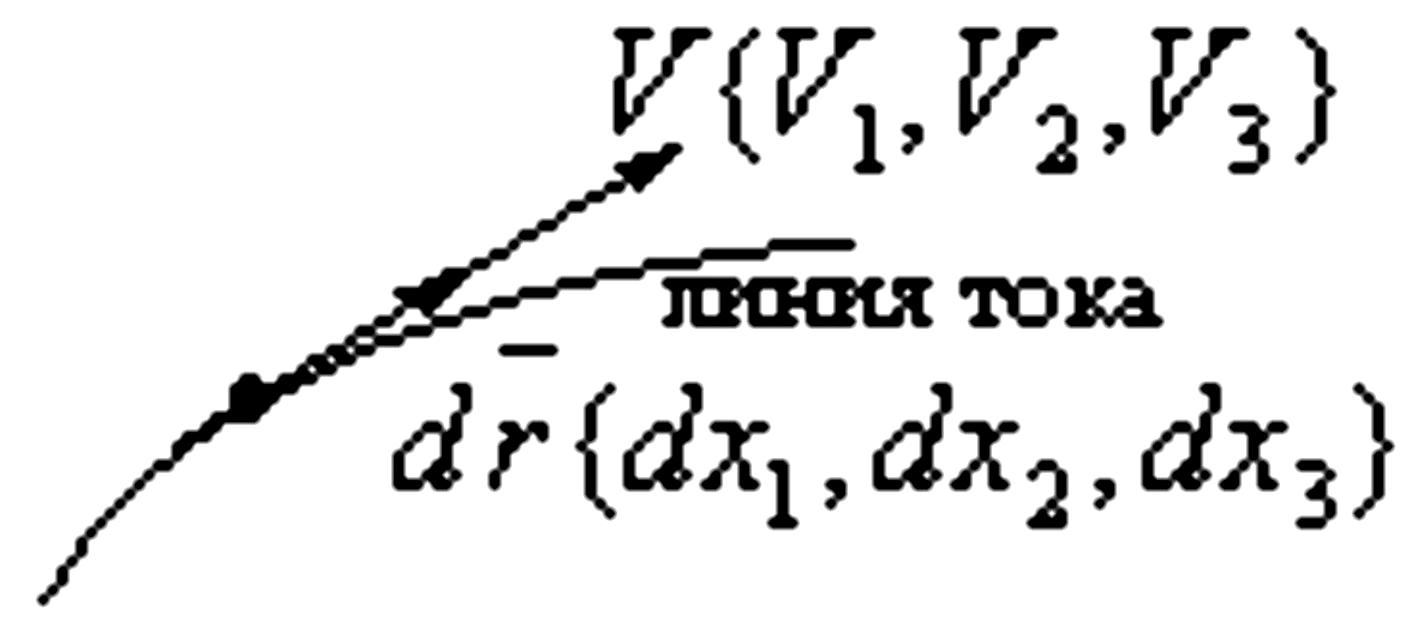

Линия тока и траектория. Линией тока в поле скорости сплошной среды (в фиксированный момент времени) называется такая кривая, в каждой точке которой вектор скорости направлен по касательной к ней. Линия тока является эйлеровой характеристикой потока; её не следует отождествлять с траекторией  геометрическим местом последовательных положений материальной точки (элементарной жидкой частицы) при её движении в пространстве, которая является лагранжевой характеристикой потока. Траектория  это путь индивидуальной частицы. Поэтому эти линии совпадают только при установившемся движении, когда поле скорости не меняется во времени, т.е. u = u (r). Если же движение неустановившееся, u = u(r,t), то эти линии не совпадают.

Важной особенностью совокупности линий тока в фиксированный момент времени является то, что они никогда не пересекаются друг с другом, за исключением особых точек (например, в случае источника - фонтана). Это следует из того, что скорость в данной точке не может быть касательной одновременно к двум пересекающимся кривым.

Рис. 3.5. Траектория движения частицы

Если элементарный вектор, касательный к линии тока, обозначить через , то вследствие того, что вектор коллинеарен , дифференциальные уравнения линий тока можно записать в виде

. (3.2.7)

Таким образом,

,

,

(при t = const).

Рис.3.6. Линии тока и траектории: а  при установившемся движении совпадают;

б  при неустановившемся движении 1,2.3  линии тока в моменты времени t, t + t₁, t + t₂. Т  траектории элементарного жидкого объёма показаны пунктиром

Особенности лагранжева и эйлерова методов описания движения сплошной среды продемонстрируем на примере установившегося движения жидкости (рис.3.6), при котором траектория и линия тока совпадают.

При лагранжевом методе (рис.3.4,а) жидкая частица, имеющая при t = t₀ начальную координату r₀ = (x₀, y₀, z₀), движется по траектории, занимая в моменты времени t₀, t₀ +t, t₀ + 2t, t₀ + 3t положения в пространстве, отмеченные на рисунке точками, то есть в параметрическом виде будем иметь .

Скорость этой частицы изменяется со временем; картина течения представляется набором траекторий различных частиц жидкости. При эйлеровом подходе тот же поток (рис.3.6,б) описывается полем скорости u = u(r,t); при установившемся движении, когда , скорость жидкости в любой точке потока зависит только от пространственных координат этой точки . Картина течения характеризуется достаточным набором линий тока.

Если выбрать произвольную кривую С, не совпадающую с линией тока, и через каждую её точку провести линию тока, то образуется поверхность тока. Если кривая С замкнута, поверхность тока превращается в трубку тока.

Аналитически семейство линий тока в проекциях выглядит следующим образом:

(i = 1,2,3). (3.2.8)

Где d  скалярный параметр. Выражение (3.2.8) – это дифференциальные уравнения линий тока.

Они отличаются от уравнений, описывающих закон движения или траектории движения частиц сплошной среды:

(i = 1,2,3), (3.2.9)

тем, что в уравнениях (3.2.8) t – параметр, а в (3.2.9) t  переменная величина.

Итак, линии тока не совпадают с траекториями. Совпадать они могут только в двух случаях:

1. При установившихся движениях (тогда между двумя последними уравнениями нет различия).

2. При неустановившихся течениях (когда поле скоростей меняется по величине, но не меняется по направлению).

Если какая-либо скалярная величина задана как функция переменных Эйлера, то в каждый момент времени можно рассматривать

поверхность, где

f (x₁ , x₂ , x₃ ,t) = const. (3.2.10)

Эта поверхность называется поверхностью равного уровня или эквипотенциальной поверхностью. Вектор, направленный по нормали в какой-либо точке М эквипотенциальной поверхности (3.2.10) в сторону роста  и равный по величине , называется вектором-градиентом скалярной функции  в точке М.

Вектор-градиент обозначается как grad  и вычисляется по формуле:

,

где  единичные векторы по направлению и вдоль координатных осей.

Проекция вектора grad  на некоторое направление определяет изменение плотностей в этом направлении:

где   угол между направлениями и ; Cos _I – направляющие косинусы вектора .

Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (3.2.10).