8.2. Моделирование движения сложных сред

Представим себе, что жидкость разделена на бесконечно тонкие горизонтальные плоские слои (рис.8.1), которые при перемещении верхней пластины скользят один по другому так же, как карты в сдвигаемой колоде. Если скорость v₀ бесконечно мала, то эта деформация не требует сколько-нибудь заметного усилия, хотя величина смещения U может расти безгранично.

Только тогда, когда скорость v₀ будет конечна, возникает сила сопротивления, вызванная трением слоев жидкости относительно друг друга. Отсюда ясно, что мерой сдвиговых деформаций жидкости является не величина , а аналогичное ей отношение , называемое

Рис.8.1. Течение вязкой жидкости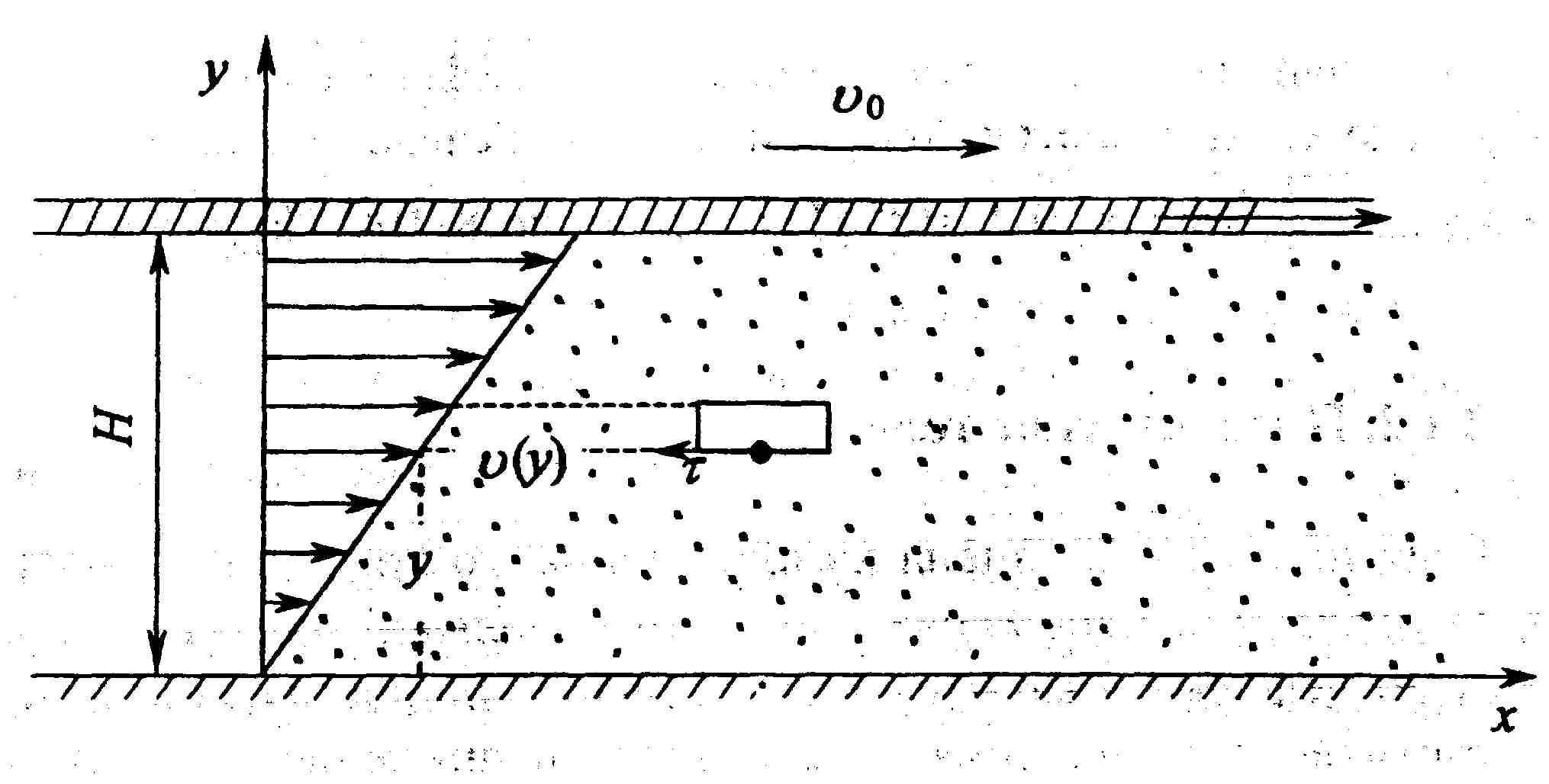

скоростью сдвига (Н  расстояние между пластинами).

Поскольку , то скорость сдвига часто обозначается символом (напомним, что в механике точка соответствует дифференцированию по времени). Силы, необходимые для сдвига жидкости, по-прежнему определяются касательным напряжением , где F  сила сопротивления, возникающая на площади S из-за затрудненного проскальзывания соседних слоев жидкости. Предполагая, что касательное напряжение пропорционально скорости сдвига (Ньютон, 1687 г.), получим , где величина  называется вязкостью жидкости.

Материалы, описываемые этим уравнением, называются ньютоновскими жидкостями. Реальные значения вязкости изменяются в очень широких пределах. Так, при 20°С вода имеет вязкость 110^-3 Пас, а глицерин  1,5 Пас.

На рис.8.2 приведены реологические кривые  зависимости касательного напряжения от меры сдвига  для трех рассмотренных выше материалов. Такие диаграммы могли бы быть получены в ходе экспериментов с идеальными телами при постепенном увеличении напряжения (нагрузке) и обратном его уменьшении (разгрузке). Стрелки на приведенных диаграммах указывают направление, в котором изменяется напряжение.

Реологическая диаграмма пластического тела имеет 1 упругий участок вплоть до предела текучести. При снятии напряжений, эта часть полной деформации обратима, а те деформации, что были накоплены в процессе течения, являются необратимыми (рис. 8.2, б).

Рис. 8.1. Реологические кривые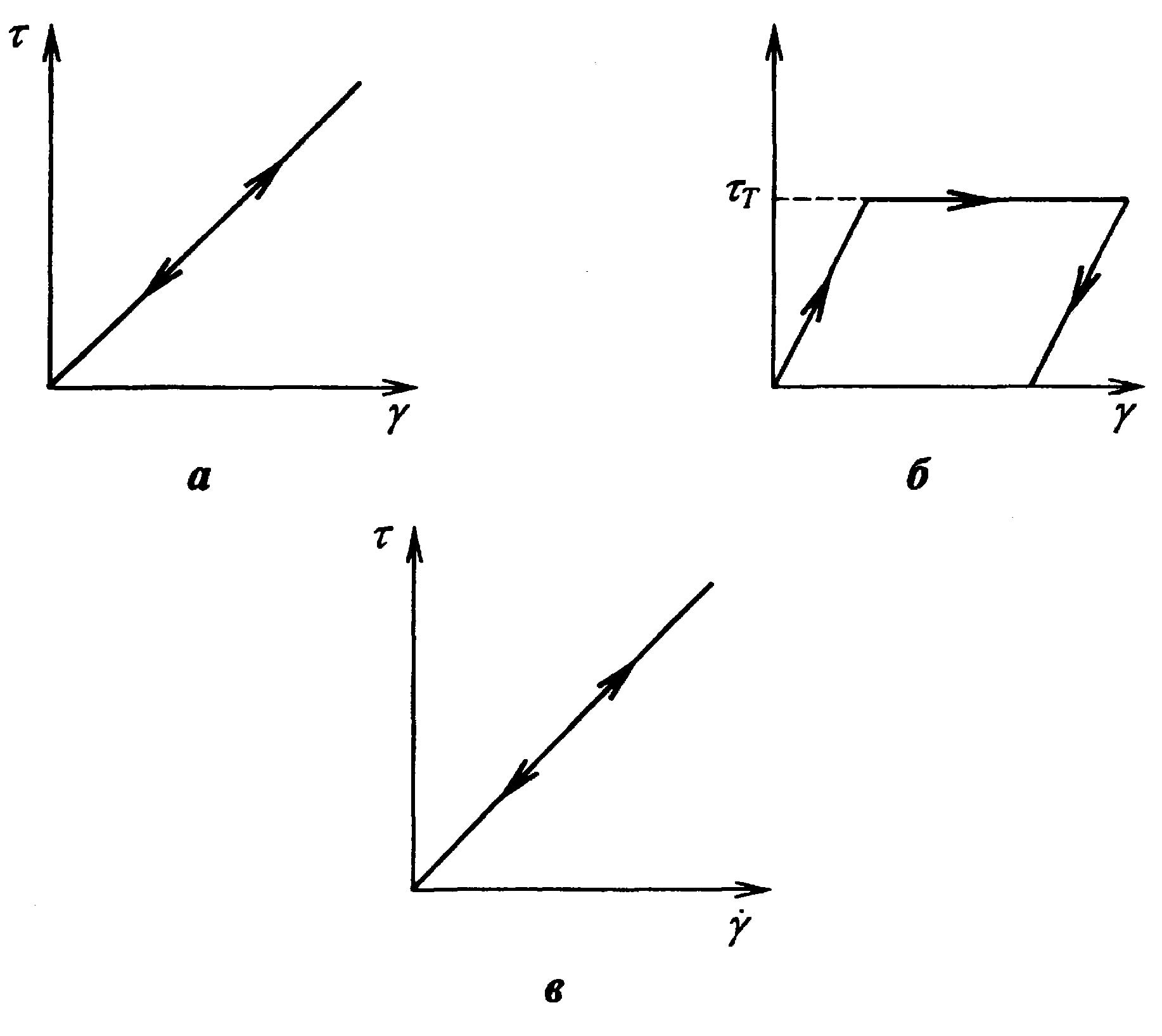

Хорошо всем знакомым примером такого тела является зубная паста. Если слегка сдавить тюбик с зубной пастой, то плоская поверхность пасты в выходном отверстии становится выпуклой, но при снятии давления эта выпуклость исчезает. Если же тюбик сжимается с большей силой, то происходит необратимое выдавливание цилиндрика пасты. Присмотревшись, можно заметить, что на конце этого цилиндрика образуется сферический сегмент, пропадающий после снятия нагрузки за счет исчезновения обратимых нагрузок.

8.2.1. Течение ньютоновской жидкости в круглой трубе

Рассмотрим ламинарное течение вязкой (ньютоновской) жидкости в круглой трубе радиуса R. При таком течении цилиндрические слои жидкости (которые должны мыслиться бесконечно тонкими) перемещаются в направлении оси трубы z, совершая "телескопическое" движение (рис. 8.2, а). Так как жидкость несжимаема, то скорость v остается постоянной по длине трубы и зависит только от расстояния r до центральной оси. Для определения зависимости составим уравнение равновесия сил, действующих на цилиндрический объем жидкости длиной l и радиусом r (рис. 8.3, б).

Сила вязкого сопротивления, действующая на внешнюю поверхность цилиндра со стороны внешних слоев, равна . Эта сила уравновешивается раз­ницей сил давления, действующих на основания цилиндра, поэтому

, откуда (8.2.1)

Рис. 8.2. Ламинарное течение

ньютоновской жидкости в трубе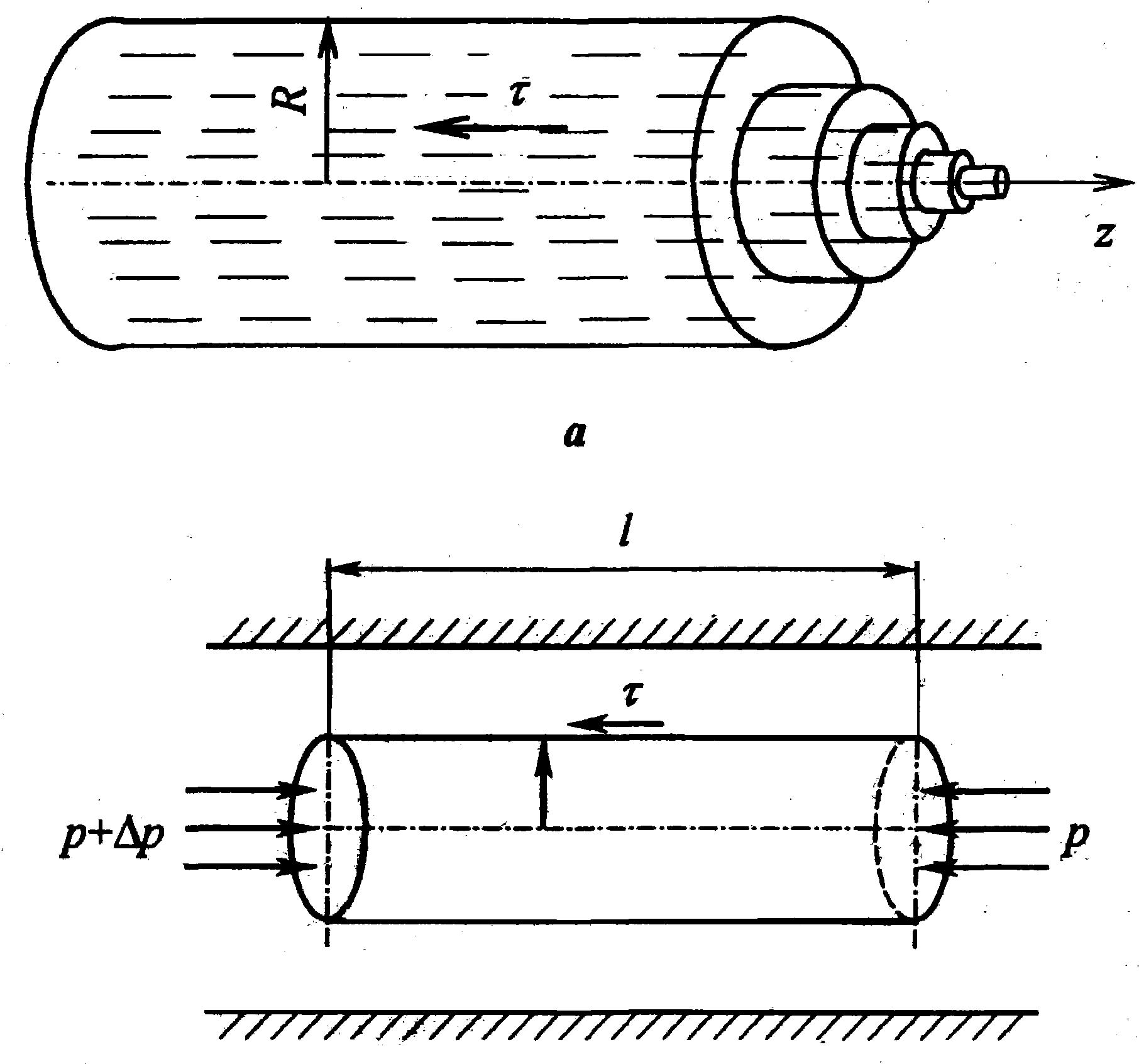

(знак "минус" означает, что сила сопротивления направлена против оси z). По закону Ньютона

, откуда

.

Интегрируя это уравнение, получаем с учетом граничного усло­вия v (R) = 0 зависимость

. (8.2.2)

Измеряемой в опытах величиной является расход Q  объем жидкости, протекающей через поперечное сечение трубы за единицу времени, поэтому вычислим эту величину. Для этого разобьем сечение трубы на узкие кольца шириной dr. Расход жидкости через кольцо с внутренним диаметром г равен

Расход через всё сечение может быть получен простым интегрированием:

(8.2.3)

Таким образом, в случае ньютоновской жидкости наблюдается линейная связь между перепадом давления и расходом жидкости.

Определив среднюю по сечению скорость V_ср  как получим отсюда

Распределение (8.2.2) было получено Стоксом (Stokes, 1849 г.) и Гагенбахом (Hagenbach, 1860 г.). Последний назвал соотношение законом Пуазейля в честь французского ученого (Poiseuille, 17971869), который в экспериментах с водой установил эмпирическую зависимость между расходом, геометрическими размерами тела и давлением.