
Методика расчета
Энергия частицы
Начальная энергия рассчитывается по следующей формуле:
![]()
Е0 – начальная энергия;
m – масса частицы;
V0 – начальная скорость.
m=4а.е.м. =4·1,66·10-27=6.64·10-27кг;
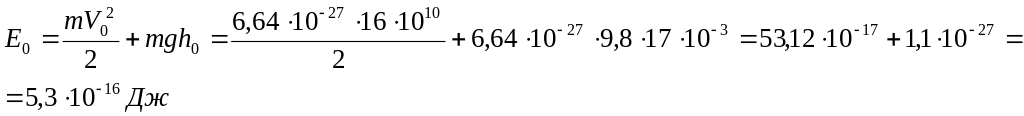 Так
как скорость иона очень велика, его
потенциальную энергию можно было не
учитывать при вычислении полной энергии.
Так
как скорость иона очень велика, его
потенциальную энергию можно было не
учитывать при вычислении полной энергии.
Ёмкость конденсатора
C=[Ф]
Величина емкости определяется геометрией конденсатора, а также диэлектрическими свойствами среды, заполняющей пространство между обкладками.
Формула для емкости плоского конденсатора следующая:
![]()
С – электроемкость плоского конденсатора;
0 – диэлектрическая проницаемость
вакуума,
![]()
-относительная диэлектрическая проницаемость вещества заполняющего зазор, =1 (воздух);
d – расстояние между обкладками;
S – площадь пластины;
l – длина пластины;
Так как пластина имеет форму квадрата, её площадь равна:
S=l2=0,42=0,16 м2;
![]() =7,074*10-11
Ф.
=7,074*10-11
Ф.
Разность потенциалов между пластинами определяется по формуле:
U=[B]
![]()
![]()
Заряд определяется по формуле
Q=[Кл]
![]()
![]() =
=![]()
Вспомогательные вычисления для построения графиков зависимостей
На движущуюся в однородном электрическом
поле конденсатора частицу действуют
две силы:
![]() (сила со стороны поля конденсатора) и
(сила со стороны поля конденсатора) и
![]() (сила тяжести). Поскольку частица заряжена
положительно, то она будет двигаться к
отрицательно заряженной пластине
конденсатора. Учитывая известные из
условия задачи направления координатных
осей, напишем уравнение для результирующей
сил
и
:
(сила тяжести). Поскольку частица заряжена
положительно, то она будет двигаться к
отрицательно заряженной пластине
конденсатора. Учитывая известные из
условия задачи направления координатных
осей, напишем уравнение для результирующей
сил
и
:
![]()
Сила, с которой электростатическое поле конденсатора действует на помещенный в него заряд q, определяется по формуле, полученной из закона Кулона:
![]()
d – расстояние между пластинами конденсатора, м
Сила тяжести вычисляется по формуле:
![]()
m – масса частицы, кг;
g – ускорение свободного падения, g =9,8 м/с2.
Сила, действующая на частицу в поле конденсатора определяется по формуле:
F=[H]
![]()
Уравнение движения частицы в проекциях на оси координат
х, у = [м]
Сила F действуют параллельно
оси ОY, поэтому проекция
ускорения на ось ОХ равна нулю:
![]() .
.
![]()
Ускорение
а=ах=ау=![]() =[м/с2]
=[м/с2]
Полное ускорение:
![]() ,
т.к.
,
т.к.
![]() то
то
![]() .
.
![]() (по 2-му закону Ньютона)
(по 2-му закону Ньютона)
![]()
Скорость
V=[м/с]
Общие уравнения для поступательного движения выглядят следующим образом:
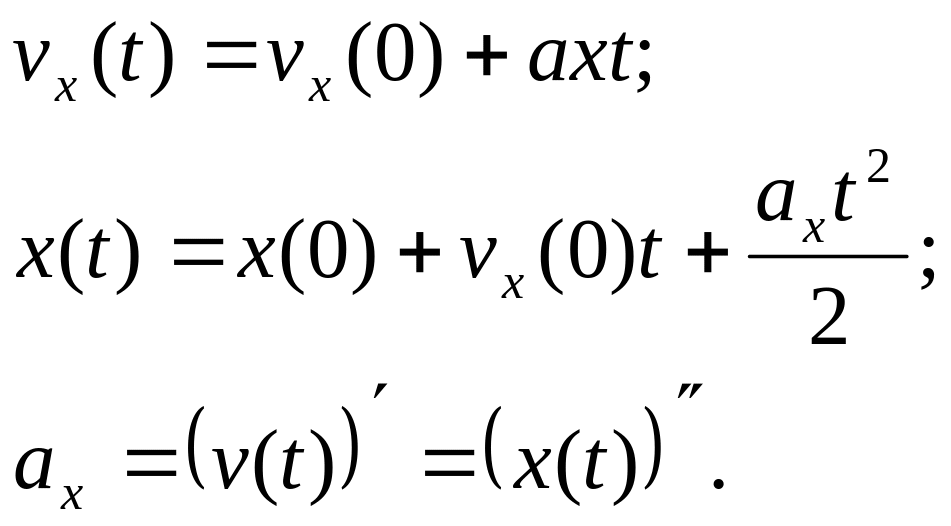
Для данного случая уравнения будут выглядеть следующим образом:
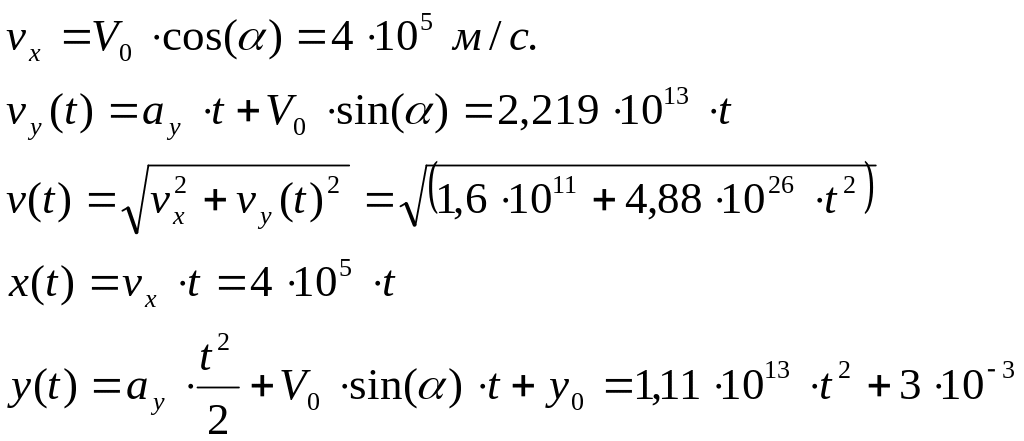
Касательное ускорение
Формула касательного ускорения выглядит следующим образом:
![]()
![]()
![]() ,
подставляем в уравнение выше и получаем
следующее:
,
подставляем в уравнение выше и получаем
следующее:

Время движения частицы
T=[c]
Максимальное перемещение по оси ОУ является расстояние между пластинами. Подставив его в уравнение движения найдем максимальное время перемещения.

Т.к. время не может быть меньше нуля, то
tmax=![]()
![]()
За время tmax=
частица пролетит по оси ОХ
![]() и по оси ОУ
и по оси ОУ
![]() м.
м.
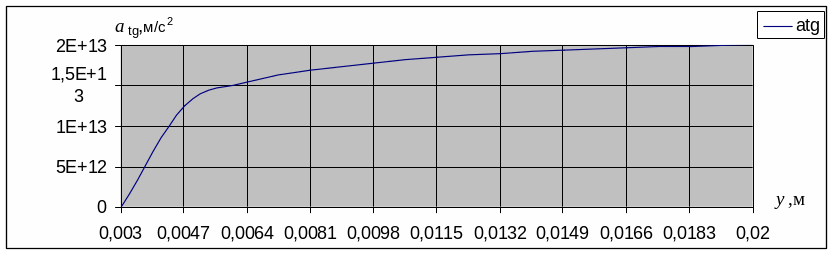
A(y) – зависимость тангенциального ускорения частицы от ее координаты “y”
Для построения графика найдём зависимость касательного ускорения от y.
Из уравнения поступательного движения имеем следующее соотношение времени от перемещения:
![]()
Сделав следующую замену:
![]() ,
получим
,
получим
![]() .
.
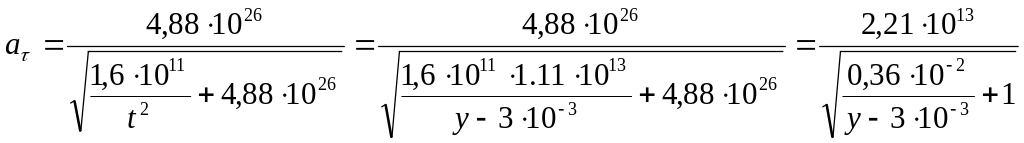
График зависимости касательного ускорения от координаты у
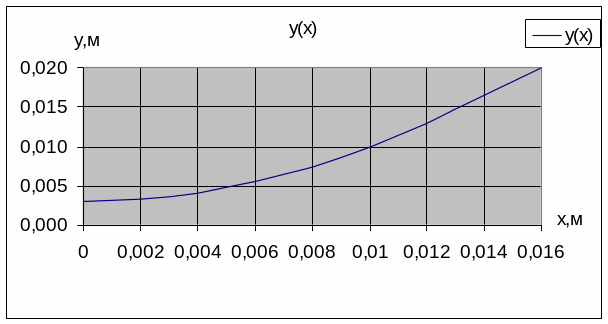
y(x) – зависимость координаты – “y” частицы от ее положения “x”;
Для построения графика найдём зависимость y от x.
Из уравнения поступательного движения имеем следующее соотношение времени от перемещения:
![]()
Через уравнение перемещения
![]() ,
заменив
,
заменив
![]() ,
получим зависимость
,
получим зависимость
![]() .
.
![]() .
.
Анализ полученного результата:
Движение частицы, после того, как она влетела в заряженный конденсатор, криволинейное;
На частицу практически не влияет сила тяжести;
Между скоростью частицы и её координатой существует прямо пропорциональная зависимость;
Между тангенциальным ускорением частицы и временем полёта её в конденсаторе существует обратно пропорциональная зависимость.
Данные, полученные мной по параметрам конденсатора– вполне соответствуют ёмкости конденсатора.
![]()
Вывод
В расчетно-графическом задании «Движение заряженной частицы в электрическом поле» рассматривалось движение иона 4He2+ в однородном электрическом поле между обкладками заряженного конденсатора. Для выполнения задания ознакомился с устройством и основными характеристиками конденсатора, также изучил движение заряженной частицы в однородном электрическом поле, а также движение материальной точки по криволинейной траектории и рассчитал необходимые по заданию параметры частицы и конденсатора:
Начальная кинетическая энергия:![]()
C – ёмкость конденсатора; C=7,074*10-11 Ф.
Q – заряд ;![]()
U –разность потенциалов
между пластинами;
![]()
Построенные графики отображают зависимости: y(x) – зависимость координаты “y” частицы от ее положения “x”; a(y) – зависимость тангенциального ускорения частицы от ее координаты “y” при этом учтено, что время полета конечно, т.к. они заканчивает свое движение на отрицательно заряженной пластине конденсатора (на верхней пластине).
