Федеральное Агентство по образованию Российской Федерации

Санкт-Петербургский Государственный Горный Институт им. Г.В. Плеханова

(технический университет)

Расчетно-графическая работа

По дисциплине: Физика

(наименование учебной дисциплины согласно учебному плану)

Тема: Движение заряженной частицы в электрическом поле

Вариант № 18

Выполнил: студент гр. ЭП-05 ______________ /Черникова Т.С../

^{(подпись) (Ф.И.О.)}

ОЦЕНКА: _____________

Дата: __________________

ПРОВЕРИЛ:

Руководитель: доцент ____________ /Стоянова Т.В./

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

2006 год.

Задание

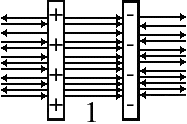
Заряженная частица ⁴He²⁺ влетает в плоский конденсатор параллельно заряженной пластине на расстоянии h₀₌17мм от отрицательно заряженной пластины.

Параметры частицы:

q – заряд;

m – масса;

V₀ – начальная скорость;

E₀ - начальная энергия.

Параметры конденсатора:

d - расстояние между пластинами;

l - длина пластины(пластина имеет форму квадрата);

Q- заряд;

U- разность потенциалов между пластинами; C- емкость;

W- энергия поля конденсатора

Численные значения параметров частицы и конденсатора:

Требуется: Определить недостающие величины. Построить графики зависимостей:

y(x) – зависимость координаты – “y” частицы от ее положения “x”;

a_(y) – зависимость тангенциального ускорения частицы от ее координаты “y”.

l

l

Рис. 1. Начальное положение частицы

Исходные данные

Параметры частицы:

Вариант	Частица	+,град.	-, град.	V0, км/с	h0, мм	E0, кэВ
18	4He2+	0	0	400	17	?

[СИ]

m, кг	q, Кл	+,град.	-, град.	V0, м\с	h0, м	E0, кэВ
6,64*10-27	3,2*10-19	0	0	4*105	17*10-3	?

Параметры конденсатора:

Вариант	d, мм	l, см	Q, мкКл	U, кВ	C, нФ	W, мДж
18	20	40	?	?	?	3

[СИ]

d, м	l, м	Q, Кл	U, В	C, Ф	W, Дж
20*10-3	0,4	?	?	?	3*10-3

Основные теоретические положения

При движении в конденсаторе для нашей частицы силой тяжести можно пренебречь по сравнению с действующей на неё силой электрического поля. Поэтому движение частицы в конденсаторе можно рассматривать как результат равномерного движения по инерции (из-за наличия массы у частицы, она будет обладать инерцией) в горизонтальном направлении и равноускоренного движения под действием силы электрического поля – в вертикальном направлении. Все силы действующие на частицу направлены вдоль оси Оy. Значит ускорение а_х будет равно нулю  а=а_у. Это ускорение имеет две составляющие: тангенциальную (а_ ) и нормальную (а_п). Первое характеризует быстроту изменения модуля скорости, второе — быстроту изменения направления скорости. Составляющие а_ и а_п перпендикулярны друг к другу. Поэтому квадрат модуля ускорения равен сум­ме квадратов модулей составляющих: Отсюда следует, что:

Конденсаторы

Электрический конденсатор- электротехническое устройство, предназначенное для накопления значительного количества разноименных электрических зарядов. Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком, толщина которого мала по сравнению с линейными размерами обкладок. Две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют плоский конденсатор.

Электроемкость плоского конденсатора.

Напряженность поля между двумя пластинами плоского конденсатора равна сумме напряженности полей, создаваемых каждой из пластин:

Если на пластинах площадью S находятся электрические заряды +q и -q, то для модуля напряженности поля между пластинами можем записать

Для однородного электрического поля связь между напряженностью E и напряжением U дается выражением , где d- в данном случае расстояние между пластинами, U- напряжение на конденсаторе.

Электроемкость конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между обкладками.

При введении диэлектрика между обкладками конденсатора его электроемкость увеличивается в раз:

Энергия заряженного конденсатора.

Если на обкладках конденсатора электроемкостью C находятся электрические заряды +q и -q, то напряжение между обкладками конденсатора равно

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0. Среднее значение напряжения в процессе разрядки равно

Для работы A, совершаемой электрическим полем при разрядке конденсатора, будем иметь:

Следовательно, потенциальная энергия W_p конденсатора электроемкостью C, заряженного до напряжения U, равна