Двоичные вычитающие счетчики

Для построения вычитающего счетчика достаточно счетные входы триггеров подключить не к инверсным, а к прямым выходам предыдущих триггеров. При этом импульсы переноса формируются при переходе триггеров из состояния 0 в состояние 1. На рис. 3.46 показана функциональная схема четырехразрядного вычитающего счетчика. Здесь в исходном положении все разряды счетчика устанавливаются в единичное состояние через установочные входы S. При подаче счетных импульсов на триггер Т₁ зафиксированное в счетчике число будет уменьшаться.

Рисунок 3.46 - Схема вычитающего счетчика

Двоичные реверсивные счетчики

Для построения реверсивного счетчика необходимо включить схемы коммутации цепей переноса с прямых выходов триггеров на инверсные и обратно. Это осуществляется обычно с помощью элементов “И” и управляющих сигналов. Пример схемы реверсивного счетчика приведен на рис. 3.47. Выбор направления счетчика здесь осуществляется значениями сигналов на управляющих шинах “Вычитание” и “Суммирование”.

Рисунок 3.47 - Схема реверсивного счетчика

3.14. Счетчики импульсов с ускоренным переносом

Основным недостатком счетчиков импульсов с последовательным переносом является их низкое быстродействие. Повышение быстродействия может быть достигнуто организацией сквозных, параллельных и групповых переносов. Принцип построения счетчиков с ускоренным переносом основан на использовании одной из особенностей двоичного счета, состоящей в возможности получения суммы при сложении двоичного числа с единицей младшего разряда в результате замены в этом числе первого нуля, считая справа налево, единицей, а всех единиц, расположенных справа от этого нуля, нулями. Например,

Рассмотрим синтез счетчиков с ускоренным переносом. Интересно заметить, что схема такого счетчика получается в результате применения теории структурного синтеза конечного автомата. Рассмотрим пример структурного синтеза счетчика с ускоренным переносом, у которого модуль счета к_сч = 8. Для отображения функционирования такого счетчика воспользуемся его алфавитными операторами, представленными таблицей переходов и выходов (таблица 3.10). В соответствии с модулем счета счетчик должен иметь 8 различных внутренних состояний от а₀ до а₇, два входных сигнала х₀ и х₁, а также два выходных сигнала y₀ и y₁.

Таблица 3.10

a(t) x(t)	a0	a1	a2	a3	a4	a5	a6	a7
x0	a0 y0	a1 y0	a2 y0	a3 y0	a4 y0	a5 y0	a6 y0	a7 y0
x1	a1 y0	a2 y0	a3 y0	a4 y0	a5 y0	a6 y0	a7 y0	a0 y1

Появление выходного сигнала соответствует поступлению на вход счетчика 8 счетных импульсов. Для получения кодированной таблицы переходов и выходов произведем кодировку входных и выходных сигналов, а также состояний счетчика. Входные сигналы счетчика Х₀ и Х₁ закодируем 0 и 1. Выходные сигналы у₀ и у₁ также закодируем 0 и 1. Для кодировки внутренних состояний счетчика необходимо использовать три элементарных автомата. В качестве элементарного автомата выберем Т-триггер, функционирование которого отображается таблицей переходов (табл.3.11), где Q(t) - внутреннее состояние элементарного автомата, а q(t) - входное воздействие на вход Т.

Таблица 3.11

q(t)	Q(t)	Q(t+1)
0	0	0
0	1	1
1	0	1
1	1	0

В связи с тем, что переходы Q(t) → Q(t+1) появляются только однажды, поэтому таблица переходов соответствует матрице переходов. Кодирование внутренних состояний счетчика представлены в таблице 3.12.

Таблица 3.12

Q1(t)	Q3(t)	Q2(t)	Q1(t)
a0	0	0	0
a1	0	0	1
a2	0	1	0
a3	0	1	1
a4	1	0	0
a5	1	0	1
a6	1	1	0
a7	1	1	1

Используя кодированную таблицу 3.12, перейдем от таблицы 3.10 к кодированной таблице переходов и выходов (таблица 3.13) и определим функции возбуждения.

Таблица 3.13

X(t)	Q3(t)	Q2(t)	Q1(t)	Q3(t+1)	Q2(t+1)	Q1(t+1)	Y(t)	q3(t)	q2(t)	q1(t)
0	0	0	0	0	0	0	0	0	0	0
0	0	0	1	0	0	1	0	0	0	0
0	0	1	0	0	1	0	0	0	0	0
0	0	1	1	0	1	1	0	0	0	0
0	1	0	0	1	0	0	0	0	0	0
0	1	0	1	1	0	1	0	0	0	0
0	1	1	0	1	1	0	0	0	0	0
0	1	1	1	1	1	1	0	0	0	0
1	0	0	0	0	0	1	0	0	0	1
1	0	0	1	0	1	0	0	0	1	1
1	0	1	0	0	1	1	0	0	0	1
1	0	1	1	1	0	0	0	1	1	1
1	1	0	0	1	0	1	0	0	0	1
1	1	0	1	1	1	0	0	0	1	1
1	1	1	0	1	1	1	0	0	0	1
1	1	1	1	0	0	0	1	1	1	1

Функции возбуждения определяются на основе анализа переходов Q_i(t) → Q_i(t + 1) + таблица переходов (табл.3.11). Для получения МДНФ проведем минимизацию функций возбуждения с помощью карт Карно, а функция выходов определяется непосредственно по кодированной таблице (рис.3.13).

Y(x) = XQ₁ ∙ Q₂ ∙ Q₃.

Это возможно по причине того, что только одна импликанта входит в эту функцию. МДНФ функций возбуждения имеет вид

q₁ = X, q₂ = XQ₁, q₃ = XQ₁Q₂,

Рисунок 3.48 - Карты Карно для функций возбуждения

Возрастание количества разрядов счетчика приведет к увеличению переменных в элементарных конъюнкциях. На рис. 3.49а показана схема параллельного переноса для 4-х разрядного счетчика, реализованного на основе выражений q_i. С целью уменьшения количества выходов у логических элементов можно произвести подстановку переменных младших разрядов в выражении для старших разрядов функций возбуждения и тогда получится схема сквозного переноса (рис.3.49б).

а) б)

Рисунок 3.49 - Схемы формирования параллельного сквозного переноса

Функциональная схема трехразрядного суммирующего счетчика со сквозным переносом изображена на рис.3.50. Каждый разряд счетчика для организации сквозного переноса содержит дополнительную схему, состоящую из элементов “И”, что позволяет обеспечить передачу сигналов переноса независимо от времени опрокидывания триггеров.

Здесь входной сигнал подается на входы С одновременно всех триггеров. Переключение любого триггера данного счетчика возможно только, если к его входу Т приложен единичный сигнал, что будет лишь тогда, когда все предшествующие триггеры исходных разрядов находятся в состоянии 1. На вход Т младшего разряда счетчика постоянно подается единичный сигнал от отдельного источника.

Длительность переходного процесса у счетчика со сквозным переносом (t_{уст.сквозной}) определяется временем переключения одного триггера и задержкой распространения сигнала в элементах “И”

t_{уст.сквозной} = t_ср.тр. + (n - 2)t_ср”и”,

так как

t_ср”и” < t_ср.тр.,

то и время установления кода меньше, чем у счетчика с последовательным переносом. Поскольку задержка сигнала в элементах “И” существенно меньше, чем в триггерах, то и время установления кода на выходных шинах, а также готовности к приему следующего счетного импульса будет меньше, чем в схеме с последовательным переносом.

Если используется серия интегральных микросхем, не содержащая элементов “И”, то в цепях переноса могут быть применены элементы “И-НЕ” с последовательным включением элементов “НЕ”, либо схемы “ИЛИ-НЕ”. В последнем случае входы вентилей “ИЛИ-НЕ” должны подключаться к инверсным выходам триггеров (на рис.3.50) показано пунктиром.

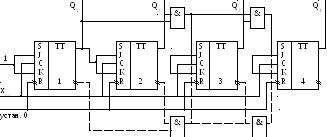
Рисунок 3.50 - Функциональная схема счетчика со сквозным переносом

Еще более высоким быстродействием обладают счетчики с параллельным или одновременным переносом (рис.3.51).

Рисунок 3.51 - Функциональная схема счетчика с параллельным переносом

Длительность переходного процесса здесь постоянна и определяется временем переключения одного триггера и задержкой сигнала в одной схеме “И”

t_ср.пар = t_ср”и” + t_{ср.триггера}.

Однако с возрастанием номера триггера прогрессивно увеличивается число входов элемента “И” входной логики. Поэтому разрядность счетчика с параллельным переносом невелика и редко превышает четыре.

В качестве компромиссного решения находят применение счетчика с групповым переносом, в котором одновременно реализуется принцип сквозного и параллельного переносов. Здесь n-разрядный счетчик разбивается на m-групп по r разрядов. Внутри каждой группы реализуется параллельный перенос, а между группами - сквозной перенос. Быстродействие такого счетчика определяется выражением

t = mt_”и” + t_{триггера}.

Функциональная схема двадцатичетырехразрядного суммирующего счетчика с групповым переносом изображена на рис.3.52. Здесь счетчик состоит из трех групп, соединенных сквозным переносом.

Рисунок 3.52 - Функциональная схема счетчика с групповым переносом

В рассмотренных типах счетчиков точно также, как и в счетчиках с последовательным переносом, счет может быть реализован по любому произвольному модулю, не обязательно равному целой степени двойки. Для этого используется метод обратной информационной связи.

3.15. Пересчетные схемы и делители частоты

В ряде случаев необходим подсчет импульсов по произвольному модулю, отличному от 2-х. Такая задача возникает, например, при построении двоично-десятичных счетчиков, делителей частоты.

Если основание пересчета счетчика не является степенью 2, то он называется пересчетной схемой, разрядность которой выбирается из условия

2^{n - 1} ≤ K_сч < 2ⁿ,

где n - число разрядов двоичного счетчика.

Принцип построения таких пересчетных схем состоит в исключении каким либо образом ряда состояний, являющихся избыточным у счетчика с К = 2ⁿ. При этом число запрещенных состояний

M = 2ⁿ - k_сч.

В зависимости от того, какие состояния счетчика выбираются в качестве запрещенных, пересчетные схемы можно подразделять на пересчетные схемы с естественным и произвольным порядком счета.

При построении пересчетных схем с естественным порядком счета используется схема с блокировкой переноса, у которой выделяется (к-1)-е состояние счетчика с последующим переводом всех триггеров в нулевое состояние.

В пересчетных схемах с произвольным порядком счета реализуются способы предварительной записи кода или принудительного порядка счета. В счетчиках с предварительной записью кода счет начинается не с нуля, а с числа m, характеризующего запрещенные состояния счетчика. После сброса счетчика в нулевое состояние выходной сигнал осуществляет запись числа m, с которого начинается счет в следующем цикле.

Синтез рассмотренных пересчетных схем проводится аналогично синтезу схем счетчиков.

Если взять за основу схему суммирующего счетчика с последовательным переносом и охватить его обратными связями, то пересчетная схема значительно упрощается, но при этом теряется быстродействие.

Для исключения избыточного состояния вводятся обратные логические связи - последовательные и параллельные. Последовательные обратные связи позволяют организовать дополнительное число коэффициентов деления. Параллельные обратные связи позволяют организовать любой К_q. Асинхронный делитель с последовательным переносом, состоящий из n-разрядов, представлен на рисунке 3.53. При подаче обратной связи ОС с n-разряда на i получаем следующие коэффициенты деления.

При ОС с n → 1 К_q = 2ⁿ - 2⁰ = 2ⁿ - 1, т.е уменьшили на единицу.

При ОС с n → 2 К_q = 2ⁿ - 2¹ =2(2^{n - 1} - 1), т.е К_q уменьшили на 2.

При ОС с n → 3 К_q = 2ⁿ - 2² = 2(2^{n - 2} - 1) и т.д.

В общем случае при подаче ОС с n-го разряда на i-й разряд (i < n) коэффициент деления будет

К_q = 2ⁿ - 2^{i - 1}.

Таким образом при использовании ОС можно получить любой К_q.

Рисунок 3.53 - Схема асинхронного делителя

На практике обычно приходится решать обратную задачу. По заданному коэффициенту деления необходимо определить схему подачи обратных связей. Эта задача сводится к нахождению номеров разрядов, на которые должна подаваться ОС, чтобы получить заданный коэффициент деления.

Для определения номеров разряда, из которых снимается обратная связь и определение номеров разрядов куда подается обратная связь, используется выражение.

N = 2ⁿ - K_сч.

При этом разница между 2ⁿ и К_сч записывается двоичным кодом, нули показывают номера разрядов, с которых берется обратная связь, а единицы - куда необходимо подать обратную связь.

Пример: Пересчетная схема с К_сч = 10. Очевидно, что пересчетная схема, имеющая 10 устойчивых состояний, должна содержать 4 элементарных автомата, так как

2³ < 10 < 2ⁿ,

тогда

n = 2ⁿ - K₁ = 16 - 10 = 6 = 0110.

Двоичный код 0110 показывает, что с нулевого и третьего разрядов необходимо взять обратную связь и подать ее на первый и второй разряды.

Синтез пересчетных схем рассмотрим на примере синтеза синхронного счетчика с последовательным переносом с К_сч = 10.

1. Определение количества триггера производится из выражения

n = | log₂ К_n |,

в нашем случае n = | log₂ 10| = 4.

2. Нахождение кода n-разрядного двоичного числа исключенных избыточных состояний определяется по выражению

М = 2ⁿ - К_сч = 2⁴ - 10 = 6 = 0110.

3. Организация обратных связей в счетчике, определяется кодом 0110.

Номера разрядов полученного двоичного кода, в которых записаны нули, совпадают с номерами триггеров, с прямых выходов которых снимается сигнал на элемент организации обратной связи, а в которых записаны единицы - с номерами триггеров, на входы которых подается сигнал обратной связи с элемента организации обратной связи. Для рассматриваемого примера обратная связь берется с триггеров ТТ₁ и ТТ₄, и подается на входы триггеров ТТ₂ и ТТ₃.

Схема счетчика приведена на рис.3.54.

Рисунок 3.54 - Схема двоично-десятичного счетчика с обратными связями

В схеме введен элемент задержки обеспечивающий задержку входных сигналов на время t_зд, превышающее длительность переходных процессов при установке триггеров в “1” по S-входам.

Так как К_сч = 10, то числу К_сч = 9 соответствует двоичный код 1001. При подаче десятого импульса Х_сч сигналом Z с выхода элемента “И-НЕ” этот код будет скорректирован до 1111. Далее задержанный импульс с выхода элемента задержки произведет сброс счетчика в нулевое состояние. Таблица переходов счетчика по модулю 10 приведена в таблице 3.14.

Таблица 3.14

Число входных импульсов	С о с т о я н и е т р и г г е р о в				Выходной сигнал
	Q4	Q3	Q2	Q1
0 1 2 3 4 5 6 7 8 9 10 11 12	0 0 0 0 0 0 0 0 1 1 1/0 0 0	0 0 0 0 1 1 1 1 0 0 1/0 0 0	0 0 1 1 0 0 1 1 0 0 1/0 0 1	0 1 0 1 0 1 0 1 0 1 1/0 1 0	1 1 1 1 1 1 1 1 1 1 0 1 1

3.16. Кольцевые счетчики

Кольцевой счетчик представляет собой замкнутый в кольцо цепью ОС сдвигающий регистр, характерной особенностью которого является то, что только один из его триггеров может находиться в состоянии “1”, а остальные - в состоянии “0”. Схема такого счетчика представлена на рис.3.55. Здесь счетные импульсы подаются на синхронизирующий вход и выполняют роль продвигающего импульса.

Рисунок 3.55 - Схема кольцевого счетчика

Порядковый номер триггера, находящегося в состоянии 1, соответствует числу счетных импульсов, поступивших на вход счетчика. На одном из входов любого триггера всегда имеется единичный сигнал, что позволяет с помощью счетных (синхронизирующего) импульсов осуществлять последовательный перевод очередного триггера в единичное состояние, а триггера, находящегося в единичном состоянии, в нулевое. При этом новое состояние триггера оказывается лишь после окончания действия счетного импульса.

Для реализации n счетных импульсов (к_сч = n) кольцевой счетчик должен содержать n - триггеров.

Перед началом работы все триггеры, кроме Т_n, устанавливаются в нулевое состояние, а Т_n - в единичное, что достигается путем подачи импульса установки исходного состояния. В том случае, когда n > 10, целесообразно вместо одного n-разрядного делителя использовать несколько делителей с меньшей разрядностью. При этом произведение их коэффициентов деления должно равняться требуемому коэффициенту деления. Применяется последовательное и параллельное соединение делителей (рис.3.56а,б). При последовательном соединении делителей (рис.3.56а) минимальное количество элементов достигается тогда, когда коэффициенты деления делителей равны между собой или мало отличаются друг от друга. При последовательном соединении счетчиков уменьшается быстродействие делителя.

а)

б)

Рисунок 3.56 - Последовательное и параллельное соединение делителей

Параллельное соединение счетчика позволяет повысить быстродействие (рис.3.56б), но может быть реализовано лишь в том случае, когда коэффициент деления равен произведению нескольких взаимно простых чисел. При этом обеспечивается однозначность деления. Выходы параллельного включения счетчиков подключаются к элементу И, на выходе которого появляется сигнал лишь в том случае, когда число будет кратно коэффициентам деления всех параллельно включенных счетчиков.

В системах связи кольцевые счетчики используются как импульсные делители частоты и элементарные коммутаторы устройств цифровой электроники. При n > 10 целесообразно вместо одного n-разрядного делителя использовать несколько делителей с меньшей разрядностью. При этом К_об = k₁ k₂ ... k_m.